Difference between revisions of "Photofission neutron rate"
| Line 4: | Line 4: | ||
=calculation= | =calculation= | ||
| − | <math>N_{1n}\propto \int \sigma_{1n}(E_{\gamma})\epsilon_{1n}(E_{\gamma})\gamma(E_{\gamma})dE_{\gamma} </math> | + | <math>N_{1n}\propto \int \sigma_{1n}(E_{\gamma})*\epsilon_{1n}(E_{\gamma})*\gamma(E_{\gamma})dE_{\gamma} </math> |
| − | <math>N_{fiss}\propto \int \sigma_{fiss}(E_{\gamma})\epsilon_{fiss}\gamma(E_{\gamma})dE_{\gamma} </math> | + | <math>N_{fiss}\propto \int \sigma_{fiss}(E_{\gamma})*\epsilon_{fiss}*\gamma(E_{\gamma})dE_{\gamma} </math> |
where, | where, | ||
Revision as of 05:54, 20 December 2016
Overview
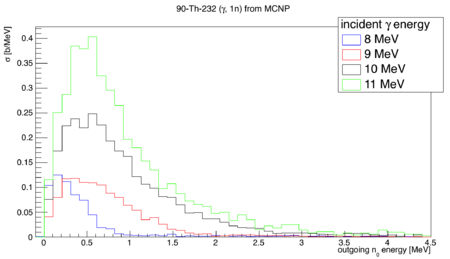
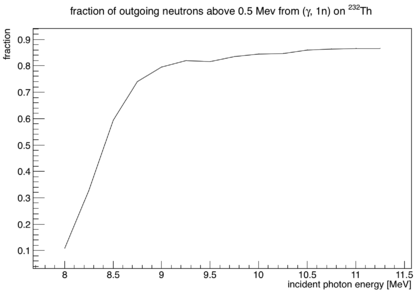
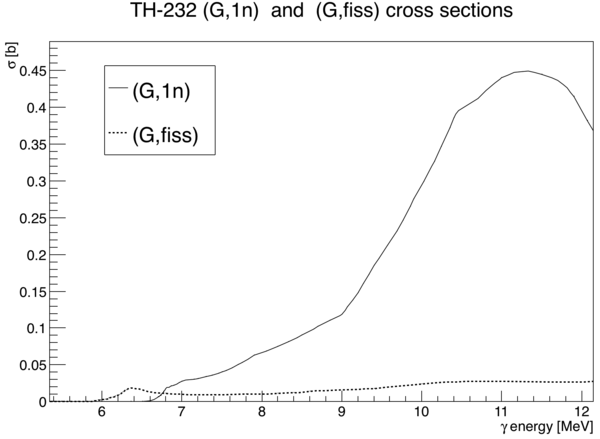
The goal of this calculation is to determine the portion of detected neutron singles that originate from photofission in a Th-232 target, as opposed to neutrons from gamma, 1n knockout. MCNP is used to determine the bremsstrahlung energy spectrum entering the experimental cell. This calculation cannot be done entirely in MCNP6 since it is missing cross section tables for Th-232 photofission. The neutron detectors are assumed to have 100% efficiency for neutrons above 0.5 MeV ,and 0% below 0.5 MeV.
calculation
where,
and are the cross-sections for 1n knockout and photofission, respectively.
is the fraction of neutrons produced from 1n knockout that are above the 0.5 MeV detection threshold.
is a constant equal to the fraction of fission neutrons above threshold, equal to 0.85.
is the bremsstrahlung photon energy distribution.