Difference between revisions of "DC hits to Moller XSection"
| Line 116: | Line 116: | ||
| − | <center><math>\Longrightarrow 29.85^{\circ}\pm .0573^{\circ}\approx | + | <center><math>\Longrightarrow 29.85^{\circ}\pm .0573^{\circ}\approx 29.88^{\circ}</math></center> |
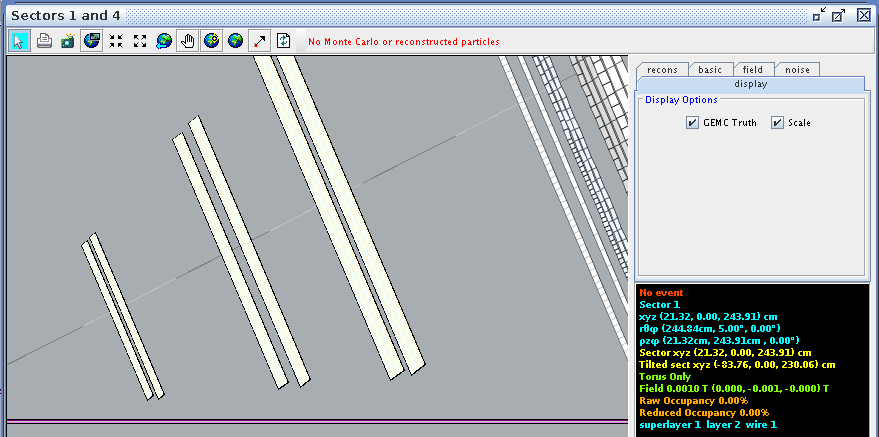
==Super Layer 1:Layer 2== | ==Super Layer 1:Layer 2== | ||
Revision as of 01:47, 27 October 2016
Verification using LUND and evio files
Examing the CM Frame Theta angles which correspond to Lab frame angles within 5-40 degrees, for only on degree in Phi (0 degrees)
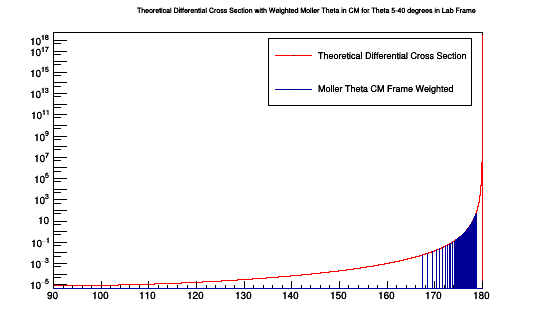
For each degree in Theta in the Lab frame, the correct kinematic variables are written to a LUND file 1000 times. These events are read from the evio file using
The Moller Scattering angle Theta is read from the evio file, and it's weight adjusted by dividing by the number it was multiplied by (1000) to give
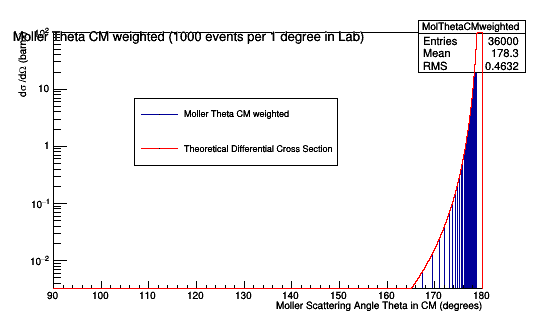
From the evio file, a histogram can be constructed that will only record the Moller events which result in hits in the drift chamber. A hit for this setting is the procID=90
Plotting the Moller scattering angle Theta in the Center of Mass frame just for on occurance of the CM angle gives the Moller Differential Cross-section.
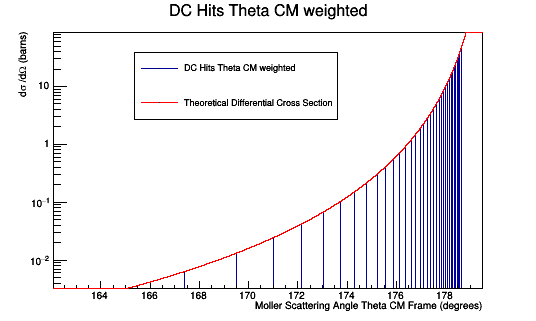
Adjusting the weight by the number of times the specific angle caused hits. We should recover the Moller differential cross-section as found previously.
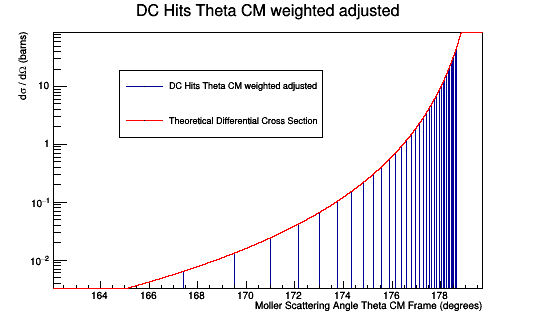
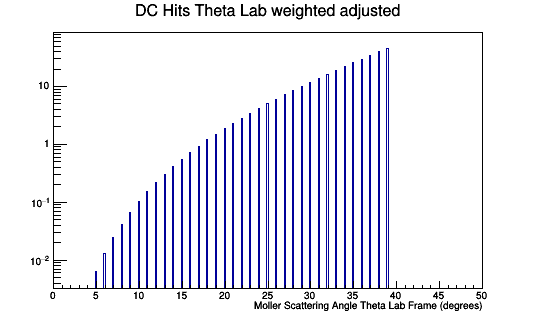
Once the validity of the Moller differential cross-section is established, we can transform from the center of mass to the lab frame as shown earlier. Since the detector is in the lab frame, the hits collected will have to be used to compose a histogram for the Moller scattering angle in the lab frame. We can show that the Moller events that register as hits in the lab matches the Moller differential cross-section in the lab.
Determining wire-theta correspondance
To associate the hits with the Moller scattering angle theta, the occupancy plots of the drift chamber hits by means of wire numbers and layer must be translated using the physical constraints of the detector. Using the data released for the DC:
DC: Drift Chambers(specs)
This gives the detector with a working range of 5 to 40 degrees in Theta for the lab frame, with a resolution of 1m radian.
This sets the lower limit:
This sets the upper limit:
Taking the difference,
Dividing by 112, we find
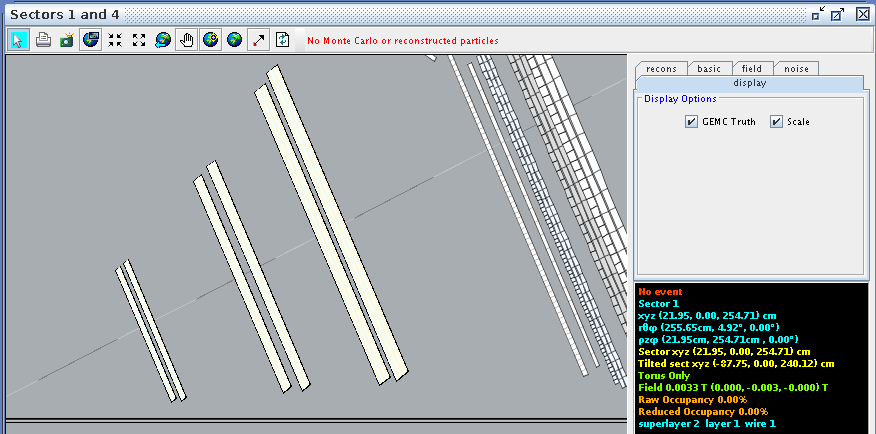
CED Verification
Using CED to verify the angle and wire correlation,
Super Layer 1:Layer 1
For a hit at layer 1, wire 1 we find the corresponding angle theta in the lab frame to be 4.91 degrees
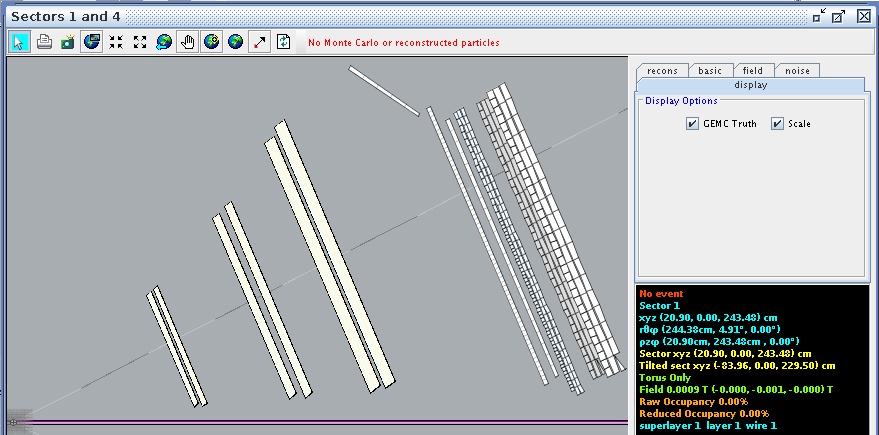
For a hit at layer 1, wire 2 we find the corresponding angle theta in the lab frame to be 5.19 degrees
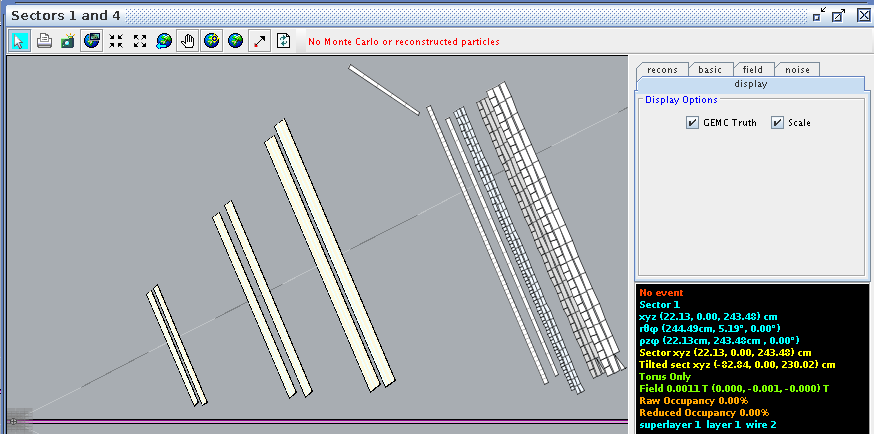
Finding the difference between the two wires,
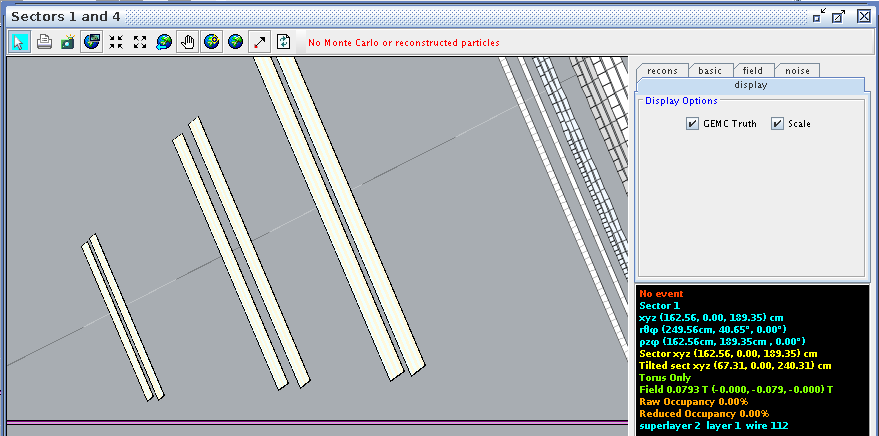
Examing a hit at layer 1, wire 112 we find the corresponding angle theta in the lab frame to be 40.70 degrees
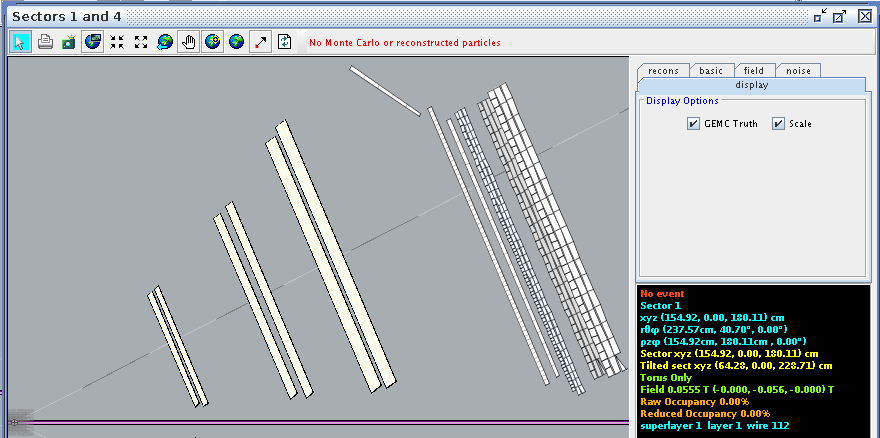
This sets the lower limit:
This sets the upper limit:
Taking the difference,
Dividing by 112, we find
Noting the difference from the spacing for a single cell, to the entire detector layer
An uncertainty of this magnitude in radians corresponds to an angular uncertainty of
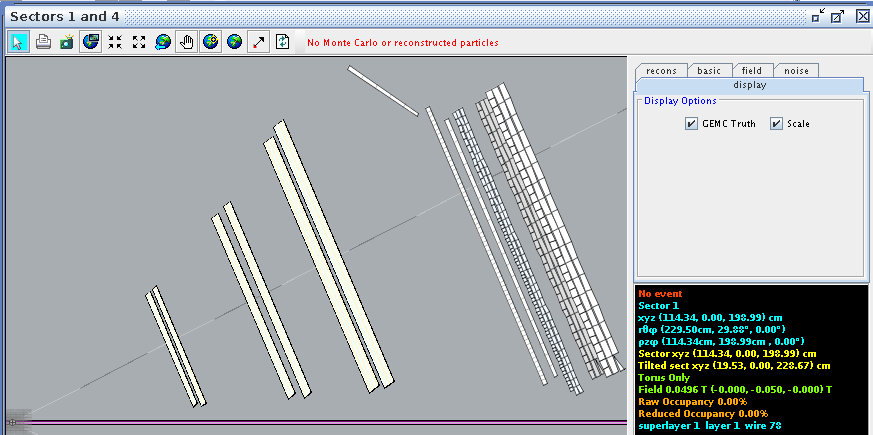
Testing this for a random angle, 78 degrees we find
Adding this to the starting angle of 4.91 degrees
Comparing this to CED at wire 78
Super Layer 1:Layer 2
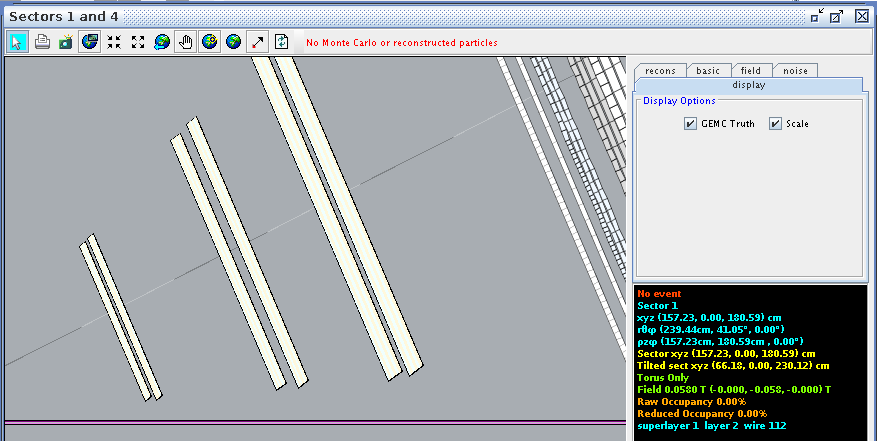
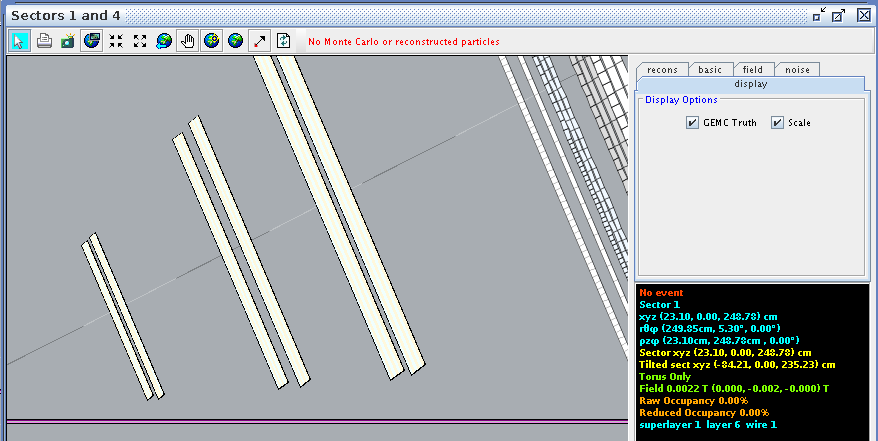
Super Layer 1:Layer 6
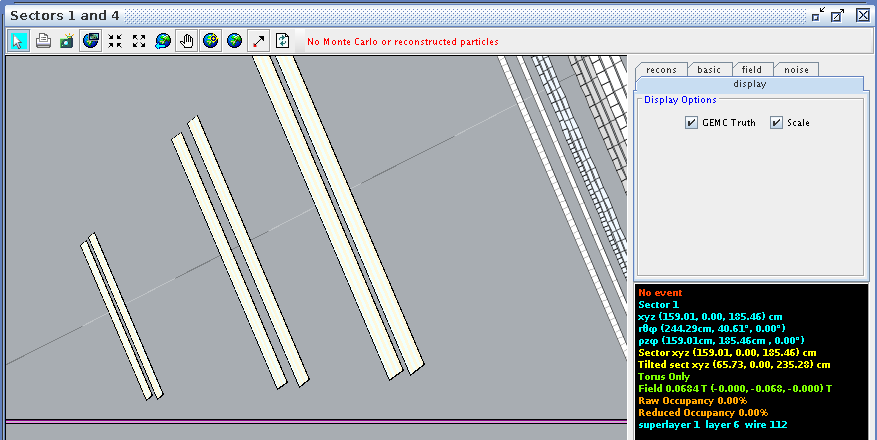
Superlayer 2:Layer 1