Difference between revisions of "Uniform distribution in Energy and Theta LUND files"
| Line 117: | Line 117: | ||
<center><math>P_z^*=\sqrt{P^{*2}-P_x^{*2}-P_y^{*2}}=\pm 53.006 MeV/c</math></center> | <center><math>P_z^*=\sqrt{P^{*2}-P_x^{*2}-P_y^{*2}}=\pm 53.006 MeV/c</math></center> | ||
| + | |||
| + | |||
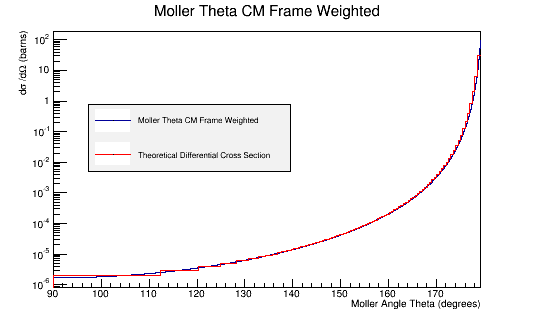
| + | [[File:MolThetaCMweightedTheory.png]] | ||
Revision as of 17:22, 24 May 2016
File:LUND Spread.C
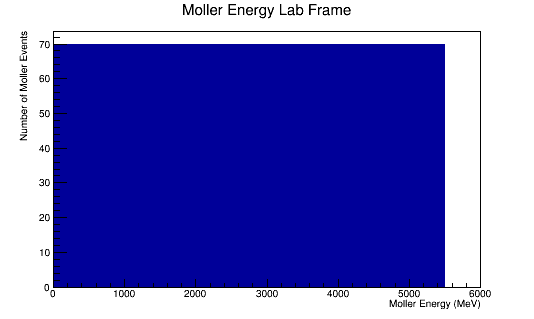
The LUND file is created by creating an isotropic distribution of particles within the energy range of 2MeV-5.5GeV as is found through GEANT simulation. These particles are also uniformly distributed through the angle theta with respect to the beam line in the range 5-40 degrees. This is done at a set angle phi (10 degrees) with respect to the perpendicular components with respect to the beam line.
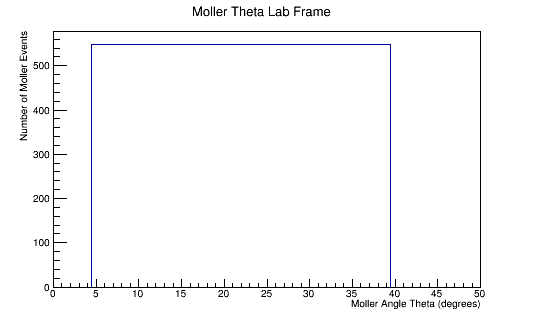
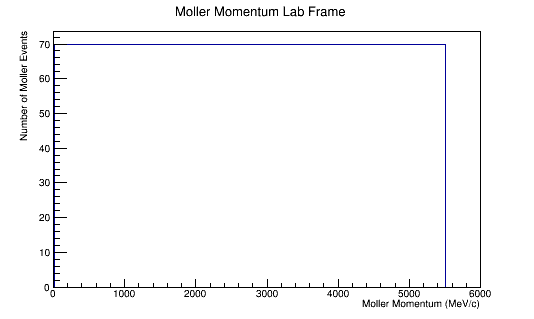
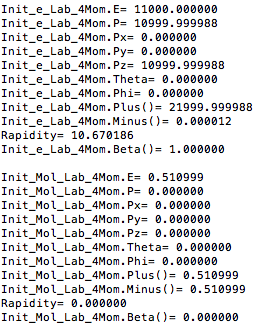
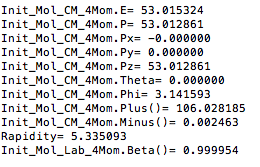
Center of Mass for Stationary Target
For an incoming electron of 11GeV striking a stationary electron we would expect:
Boosting to the Center of Mass Frame:
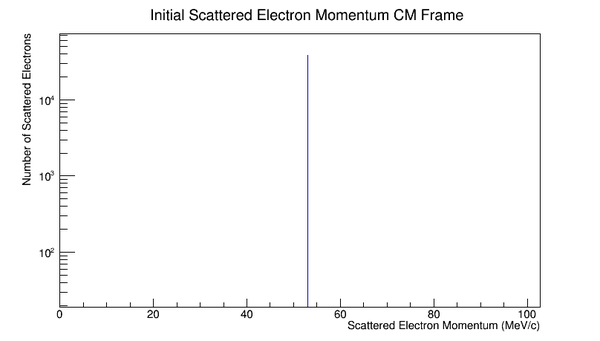
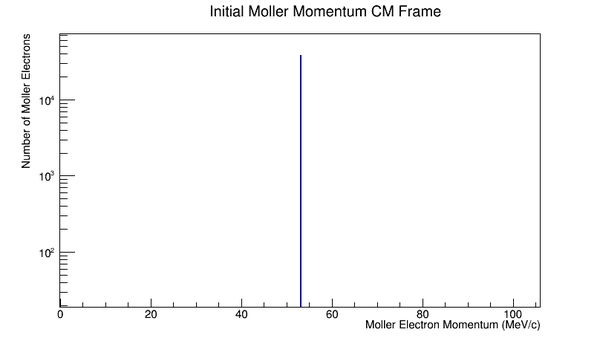
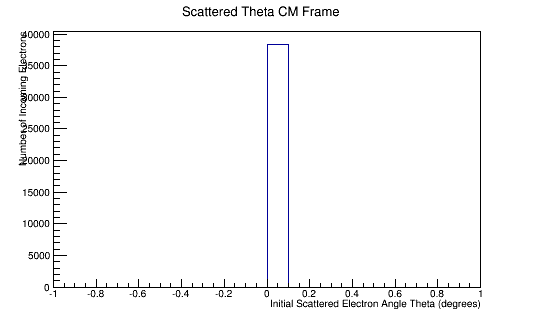
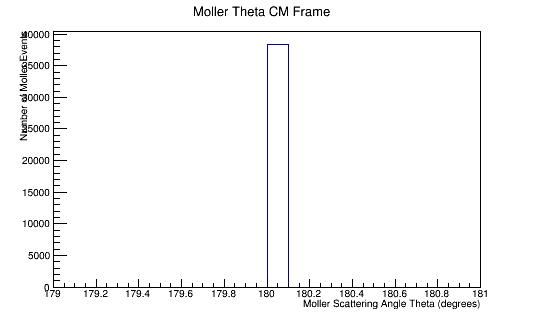
Phase space Limiting Particles
Since the angle phi has been constrained to remain constant, the x and y components of the momentum will increase in the positive first quadrant. This implies that the z component of the momentum must decrease by the relation:
In the Center of Mass frame, this becomes:
Since the momentum in the CM frame is a constant, this implies that pz must decrease. For phi=10 degrees:
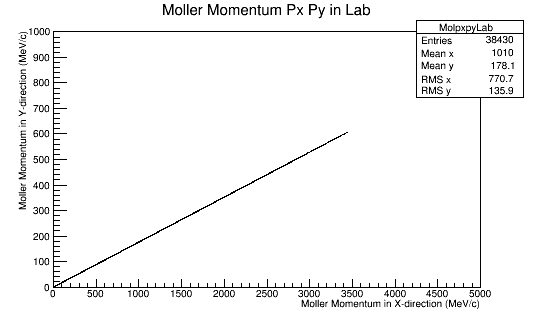
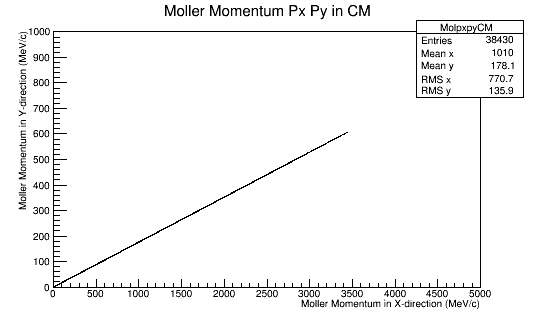
This is repeated for rotations of 60 degrees in phi in the Lab frame.
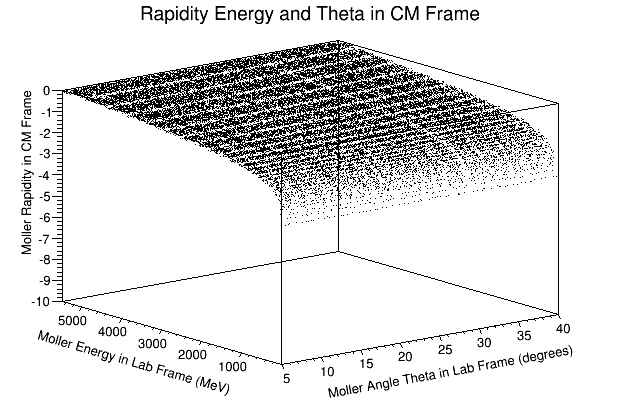
We can use the variable rapidity:
where
this implies that as
For forward travel in the light cone:
For backward travel in the light cone:
For a particle that transforms from the Lab frame to the CM frame where the particle is not within the light cone:
These particles are outside the light cone and are more timelike, thus not visible in normal space. This will reduce the number of particles that will be detected.
Using Initial Condition based on After Collision in Lab Frame
Starting with an initial Energy (10MeV), an initial angle Theta (5 degrees),and a Phi angle of 10 degrees, the 4-momentum vector can be kinematically determined:
Using the fact that the angle Theta is defined to be in the xz plane:
Using the fact that phi is defined in the xy plane to be:
We can use the Mandelstram variable s, which is a Lorentz invariant, to find the energy in the center of mass frame where the total momentum is zero.
Since the two particles are identical mass, this implies that they should have equal energy in the Center of Mass frame:
Momentum in this frame can be found using the relativistic expression for energy
Since only the z component is affected by the Lorentz transformation, we know that the x and y components will remain the same in both the lab frame and Center of Mass frame.
We can determine the z component with