Difference between revisions of "Uniform distribution in Energy and Theta LUND files"
| Line 142: | Line 142: | ||
| − | This 4 vector of the Moller electron and the scattered electron are along the original vector in the x, y, and z cartesian coordinates, which have been transformed into just motion along the z' ' axis. From this, we can boost to the Center of Mass frame, however it will be in the after collision stage. | + | This 4 vector of the Moller electron and the scattered electron are along the original vector in the x, y, and z cartesian coordinates, which have been transformed into just motion along the z' ' axis. From this, we can boost to the Center of Mass frame, however it will be in the after collision stage. Boosting only the z component by the beta factor, |
| + | |||
| + | [[File:Screen_Shot_2016-05-12_at_11.44.42_PM.png]] | ||
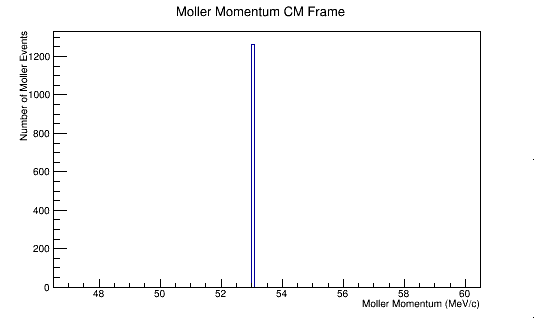
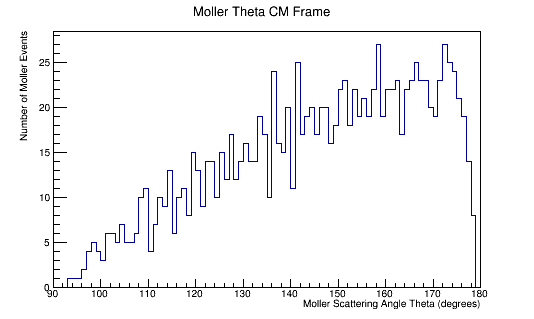
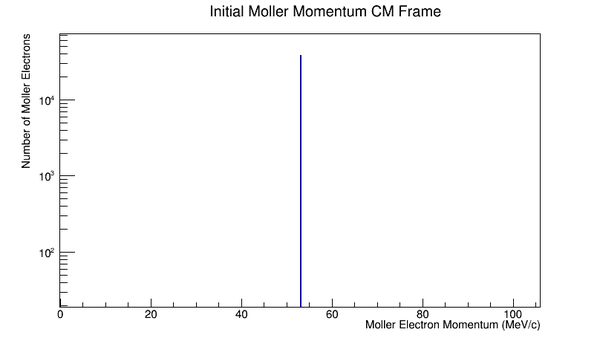
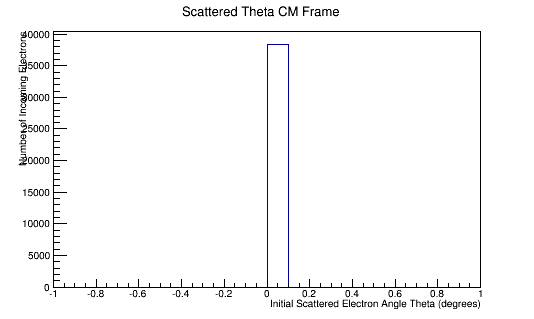
<center>[[File:Reduced_MolMomCM.png|600 px]][[File:Reduced_MolThetaCM.png|600 px]]</center> | <center>[[File:Reduced_MolMomCM.png|600 px]][[File:Reduced_MolThetaCM.png|600 px]]</center> | ||
Revision as of 05:48, 13 May 2016
File:LUND Spread.C
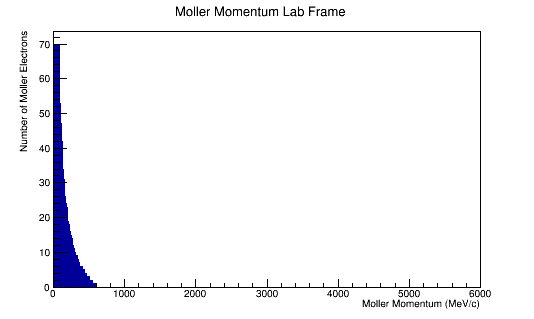
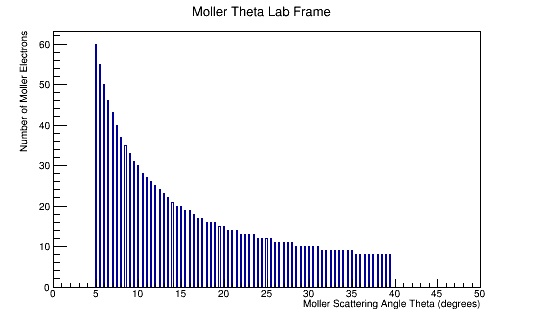
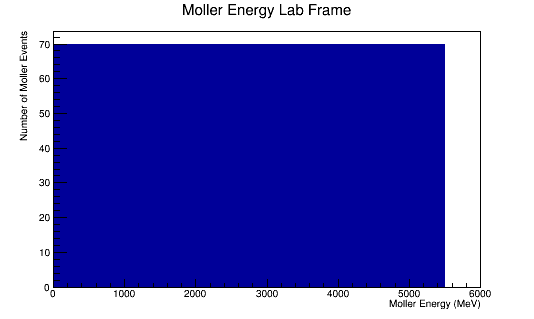
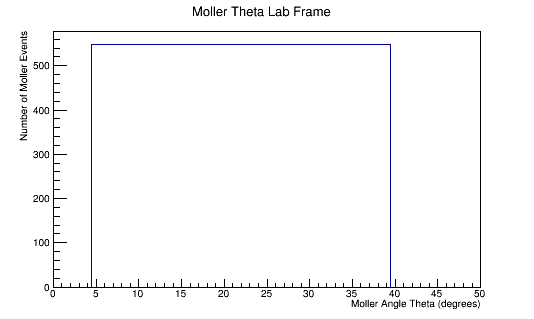
The LUND file is created by creating an isotropic distribution of particles within the energy range of 2MeV-5.5GeV as is found through GEANT simulation. These particles are also uniformly distributed through the angle theta with respect to the beam line in the range 5-40 degrees. This is done at a set angle phi (10 degrees) with respect to the perpendicular components with respect to the beam line.
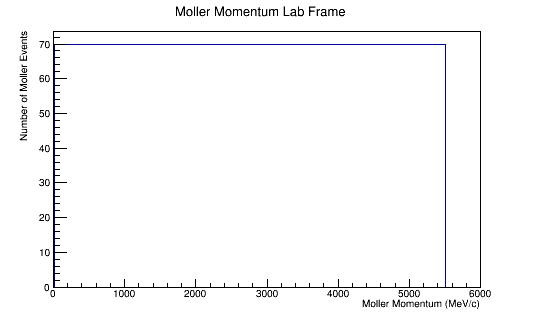
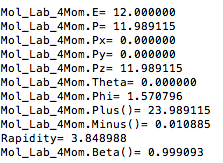
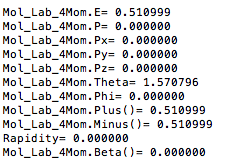
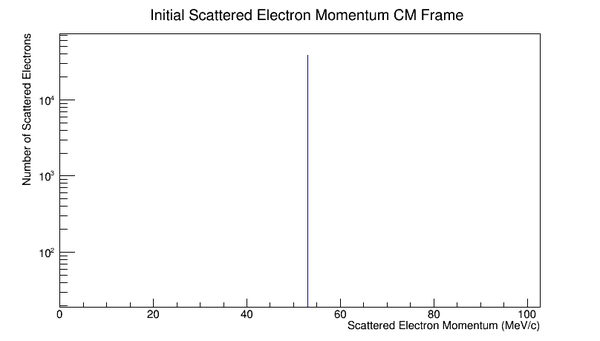
Center of Mass for Stationary Target
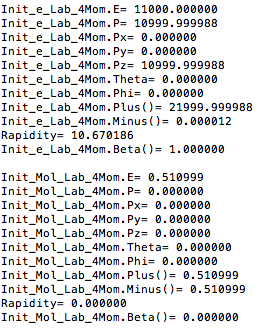
For an incoming electron of 11GeV striking a stationary electron we would expect:
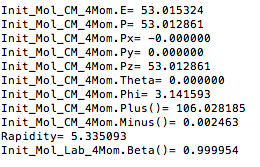
Boosting to the Center of Mass Frame:
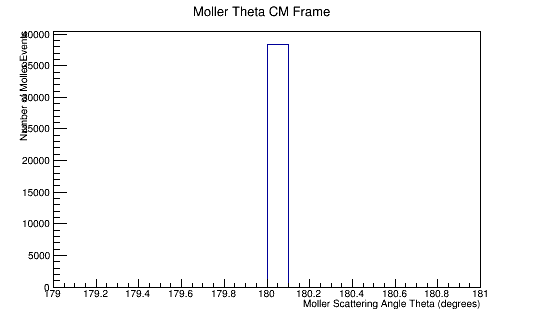
Phase space Limiting Particles
Since the angle phi has been constrained to remain constant, the x and y components of the momentum will increase in the positive first quadrant. This implies that the z component of the momentum must decrease by the relation:
In the Center of Mass frame, this becomes:
Since the momentum in the CM frame is a constant, this implies that pz must decrease. For phi=10 degrees:
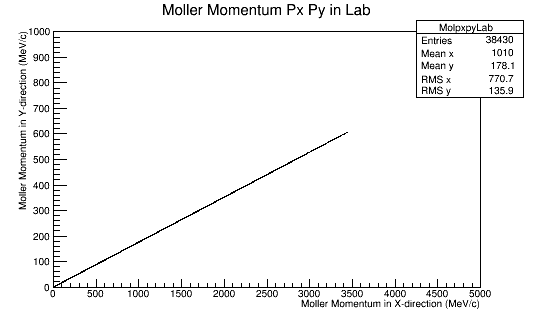
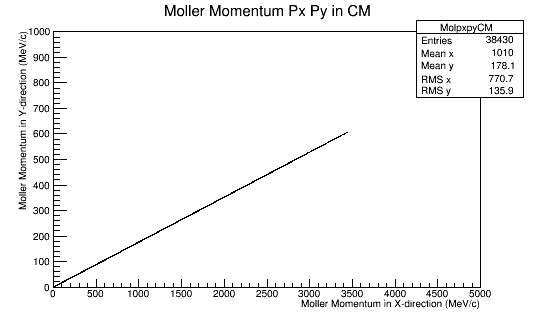
This is repeated for rotations of 60 degrees in phi in the Lab frame.
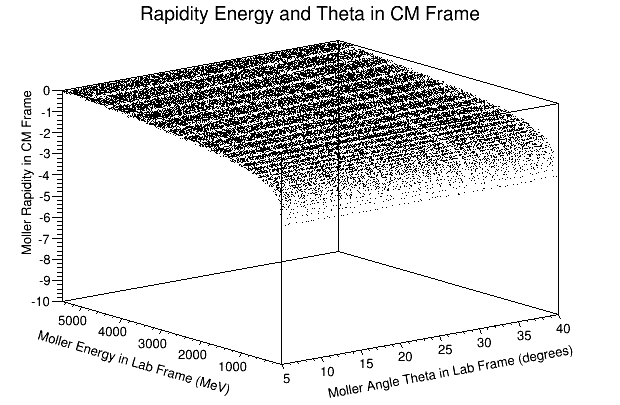
We can use the variable rapidity:
where
this implies that as
For forward travel in the light cone:
For backward travel in the light cone:
For a particle that transforms from the lab frame to a CM frame with the particle inside the light cone:
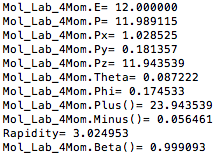
Mol_Lab_4Mom.E= 92.000000 Mol_Lab_4Mom.P= 91.998581 Mol_Lab_4Mom.Px= 51.943569 Mol_Lab_4Mom.Py= 9.159060 Mol_Lab_4Mom.Pz= 75.377159 Mol_Lab_4Mom.Theta= 0.610556 Mol_Lab_4Mom.Phi= 0.174533 Mol_Lab_4Mom.Plus()= 167.377159 Mol_Lab_4Mom.Minus()= 16.622841 Beta= 0.999985 Gamma= 180.041258 Rapidity= 1.154736 Mol_CM_4Mom.E= 53.015377 Mol_CM_4Mom.P= 53.012917 Mol_CM_4Mom.Px= 51.943569 Mol_CM_4Mom.Py= 9.159060 Mol_CM_4Mom.Pz= -5.324148 Mol_CM_4Mom.Theta= 1.671397 Mol_CM_4Mom.Phi= 0.174533 Mol_CM_4Mom.Plus()= 47.691229 Mol_CM_4Mom.Minus()= 58.339525 Rapidity= -0.100766
For a particle that transforms from the Lab frame to the CM frame where the particle is not within the light cone:
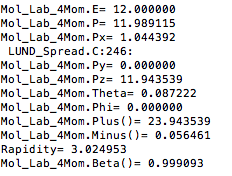
Mol_Lab_4Mom.E= 92.000000 Mol_Lab_4Mom.P= 91.998581 Mol_Lab_4Mom.Px= 52.589054 Mol_Lab_4Mom.Py= 9.272868 Mol_Lab_4Mom.Pz= 74.914246 Mol_Lab_4Mom.Theta= 0.619278 Mol_Lab_4Mom.Phi= 0.174533 Mol_Lab_4Mom.Plus()= 166.914246 Mol_Lab_4Mom.Minus()= 17.085754 Beta= 0.999985 Gamma= 180.043077 Rapidity= 1.139618 Mol_CM_4Mom.E= 53.015377 Mol_CM_4Mom.P= nan Mol_CM_4Mom.Px= 52.589054 Mol_CM_4Mom.Py= 9.272868 Mol_CM_4Mom.Pz= nan Mol_CM_4Mom.Theta= nan Mol_CM_4Mom.Phi= 0.174533 Mol_CM_4Mom.Plus()= nan Mol_CM_4Mom.Minus()= nan Rapidity= nan
These particles are outside the light cone and are more timelike, thus not visible in normal space. This will reduce the number of particles that will be detected.
Using Initial Condition based on After Collision in Lab Frame
Starting with the Energy, and a Phi angle of 10 degrees, the 4-momentum vector can be kinematically determined:
Rotating about the z-axis by negative Phi angle, we can eliminate any y-axis component by expressing the vector in x' and z' axis components.
Similarly, by then rotating about the y-axis by negateive Theta, we can express the vector in z' ' components only
This 4 vector of the Moller electron and the scattered electron are along the original vector in the x, y, and z cartesian coordinates, which have been transformed into just motion along the z' ' axis. From this, we can boost to the Center of Mass frame, however it will be in the after collision stage. Boosting only the z component by the beta factor,