Difference between revisions of "Niowave 11-2015"
| Line 37: | Line 37: | ||
|+ Energy deposited (MeV) in a 1 m long 3.48 cm diameter beam pipe surrounding a 2 mm target located at Z=-900 mm. | |+ Energy deposited (MeV) in a 1 m long 3.48 cm diameter beam pipe surrounding a 2 mm target located at Z=-900 mm. | ||
|} | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
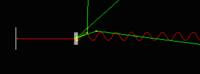
| + | The energy deposited by electrons scattered into a 1.65 mm thick stainless steel beam pipe from the LBE target as a function of a uniform solenoidal magnetic field was investigated for a 3.48 diameter stainless steel beam pipe. The simulation program GEANT4 was used to determine the amount of energy an electron lost in the stainless steel beam pipe. The beam pipe surface was divided into unit squares that were a centimeter in length and the energy deposited by a sample of 5 million electrons was summed for each unit square. The left side figure below shows a predicted peak energy deposition of 0.35 MeV/e^- in the 1.65 mm thick stainless steel beam pipe per 10 MeV electron impinging the 2 mm thick LBE target that has been sandwiched between two 0.25 mm thick stainless steel windows. | ||
| + | |||
| + | The energy deposited in the beam pipe can be converted to an average heat load if a average beam current is assumed. | ||
| + | Under the assumption of a 1mA (10^-3 C/s) average beam current, the deposited energy (E_{dep}) per cm^2 per electron can be converted to the deposited power (P) per area using the equation | ||
| + | |||
| + | <math>P= E_{dep} \left( \frac{\mbox{MeV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right ).</math> | ||
| + | |||
| + | In other words, the energy deposited in units of keV/cm^2/e by a 1 mA electron beam is equivalent to a heat load in the units of Watts per cm^2. | ||
| + | |||
| + | <math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )</math> | ||
| + | |||
| + | Based on this observation the peak heat load, as shown in the figure below on the right, for a 1 mA electron beam is 35 W/cm^2. The electrons will begin to intersect a 3.48 diameter beam pipe less when the solenoidal magnetic field strength increases beyond one Tesla. A solenoidal field between two and four Tesla would substantially reduce the electron heat load on the beam pipe and place the positrons in a tight helical orbit for transportation. | ||
| + | |||
| + | |||
| + | add units to the histograms below | ||
| + | |||
| + | {| border="1" | ||
| + | | [[File:BeamPipeDepEmev-vs-B.png |200px]] || [[File:BeamPipeDepPower-vs-B.png |200px]] | ||
| + | |+ Energy deposited (MeV) along a 1 m long beam pipe of stainless steel 1.65 mm thick. | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Revision as of 15:13, 13 April 2016
A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -902 mm. Niowave Positron Project Progress for November 2015
The next step in the positron project, after determining the PbBi thickness for maximum positron production, was to estimate the heat that would be deposited from the primary electron beam on the beam pipe. Electrons scattered by the PbBi target will intersect a beam pipe used to transport the desired positrons. Electrons traversing the beam pipe can deposit energy that will heat the beam pipe. The goal of this simulation was to estimate the amount of the deposited energy to determine if there is sufficient cooling to prevent a beam pipe breach. Below is a preliminary design of the beam pipe dimensions.
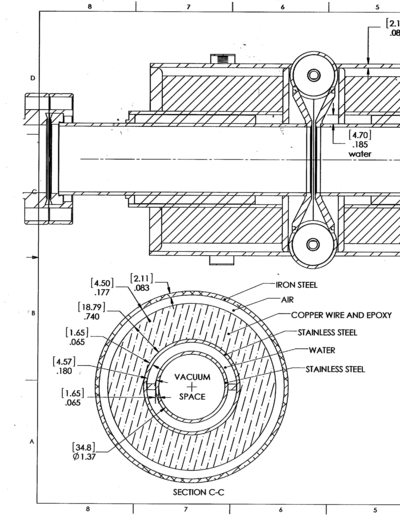
| Element | dimension |
| Inner beam pipe radius | 1.74 cm |
| Inner beam pipe thickness | 0.165 cm |
| water jacket thickness | 0.457 cm |
| outer beam pipe radius | 2.362 cm |
| outer beam pipe thickness | 0.165 cm |
| Solenoid inner radius | 2.527 cm |
| Solenoid outer radius | 4.406 cm |
A comparison between the prediction from MCNPX and GEANT4 was once again performed. As shown in the figure below, GEANT4 predicts a peak energy deposition of 0.35 MeV/e while MCNPX predicts about 0.38 MeV/e. GEANT4 predicts a total of MeV (the integral adds up the energy in each 1cm bin) of energy will be deposited in a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target.
 |

|
The energy deposited by electrons scattered into a 1.65 mm thick stainless steel beam pipe from the LBE target as a function of a uniform solenoidal magnetic field was investigated for a 3.48 diameter stainless steel beam pipe. The simulation program GEANT4 was used to determine the amount of energy an electron lost in the stainless steel beam pipe. The beam pipe surface was divided into unit squares that were a centimeter in length and the energy deposited by a sample of 5 million electrons was summed for each unit square. The left side figure below shows a predicted peak energy deposition of 0.35 MeV/e^- in the 1.65 mm thick stainless steel beam pipe per 10 MeV electron impinging the 2 mm thick LBE target that has been sandwiched between two 0.25 mm thick stainless steel windows.
The energy deposited in the beam pipe can be converted to an average heat load if a average beam current is assumed. Under the assumption of a 1mA (10^-3 C/s) average beam current, the deposited energy (E_{dep}) per cm^2 per electron can be converted to the deposited power (P) per area using the equation
In other words, the energy deposited in units of keV/cm^2/e by a 1 mA electron beam is equivalent to a heat load in the units of Watts per cm^2.
Based on this observation the peak heat load, as shown in the figure below on the right, for a 1 mA electron beam is 35 W/cm^2. The electrons will begin to intersect a 3.48 diameter beam pipe less when the solenoidal magnetic field strength increases beyond one Tesla. A solenoidal field between two and four Tesla would substantially reduce the electron heat load on the beam pipe and place the positrons in a tight helical orbit for transportation.
add units to the histograms below
 |

|
if you assume a 1 mA beam of electrons then this becomes
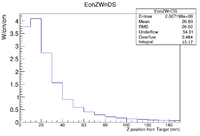
I converted the above histogram to deposited power by 1000 mA, divide by the number of incident electrons, divide by the circumference of the beam pipe, convert the number of electrons to Coulombs, and use a unit conversion from MeV to W-s per MeV.
If you use the above factors to weight the histogram, then the figure below shows that GEANT4 predicts a power deposition density of , 1 cm downstream of the target. Back scattered electrons appear to create the hottest spot of about 1cm upstream of the target.
 |

|
| Power Deposition Zoomed in and 902 mm offset applied | Power deposition over the 1 m long beam pipe |
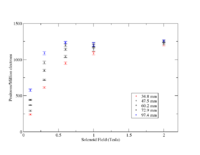
The energy deposited by electrons scattered into a 3.48 diameter stainless steel beam pipe (1.65 mm thick) from a PbBi target as a function of a uniform Solenoidal magnetic field.
| B-field (Tesla) | Hot Spot () |
| 0.0 | 0.35 |
| 0.3 | 0.35 |
| 1.0 | 0.35 |
| 1.5 | 0.22 |
| 2.0 | 0.10 |
| 4.0 | 0.002 |
To convert this deposited energy per incident electron on the target to a heat load in the pipe you need to divide by the area of the pipe.
A histogram is filled with 1 cm bins along the Z axis. The surface area becomes . The beam pipe diameter assumed is 3.48 cm.
When filling the histogram binned 1 cm in Z, you should weight it by the amount of depositred energy divided by the circumference of the pipe and divided by the number of incident electrons on the target (5 million). The energy units are converted to keV by multiplying the numberator by 100 or in this case dividing by 5000 instead of 5 million.
TH1F *T00N=new TH1F("T00N","T00N",100,-1000.5,-0.5)
Electrons->Draw("evt.EoutPosZ>>T00N","evt.DepE/10.088/5000")
To convert From Mev/ e- to kW/cm^2 assuming a current of 1mA (10^-3 C/s) you
 |
 |

|
With SS windows
Positrons->Draw("sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)","evt.BeamPosMomZ>0 && evt.BeamPosPosZ>-500 && sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)<97.4/2");
Positron Collection rates with 60 cm long Solenoid
With SS windows
Positrons->Draw("sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)","evt.BeamPosMomZ>0 && evt.BeamPosPosZ>-500 && sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)<97.4/2");
| B-field (Tesla) | 34.8 mm diameter pipe | 47.5 | 60.2 | 72.9 | 97.4 | |
| 0.0 | 0.35 | 1,2,4,4,5 | 2,3,4,4,6 | 4,4,6,7,9 | 6,8,9,10,11 | 16,14,15,16,17 |
| 0.1 | 225,236,250,246,249=241 10 | 282,282,293,294,306=291 10 | 373,366,370,364,373=369 4 | 451,437,440,438,451=443 7 | 602,584,563,558,570=575 18 | |
| 0.3 | 0.35 | 626,619,596,619,611 =614 11 | 720,726,706,730,717=720 9 | 871,864,840,841,834 =850 16 | 987,968,939,943,952 =958 20 | 1118,1106,1069,1067,1080=1088 23 |
| 0.6 | 929,935,949,969,961=949 17 | 1022,1031,1046,1059,1052 =1042 15 | 1120,1130,1152,1154,1146 =1140 15 | 1168,1184,1210,1221,1206 =1198 21 | 1212, 1218,1240,1254,1242=1233 18 | |
| 1.0 | 0.35 | 1117,1085,1083,1061,1085=1086 20 | 1188,1154,1140,1111,1134=1145 28 | 1225,1190,1178,1149,1172 =1183 28 | 1243.1208,1195,1164,1184=1199 30 | 1252,1219,1206,1178,1200=1211 27 |
| 1.5 | 0.22 | |||||
| 2.0 | 0.10 | 1198,1210,1215,1223,1176=1204 18 | 1216,1227,1235,1241,1196 =1223 18 | 1237,1243,1252,1257,1214=1241 17 | 1249,1252,1262,1266,1225 =1251 16 | 1257,1262,1270,1276,1234=1260 16 |
| 4.0 | 0.002 |
|