PbBi BeamPipeHeatin 2015

A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -902 mm.

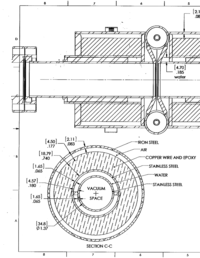
Element	dimension
Inner beam pipe radius	1.74 cm
Inner beam pipe thickness	0.165 cm
water jacket thickness	0.457 cm
outer beam pipe radius	2.362 cm
outer beam pipe thickness	0.165 cm
Solenoid inner radius	2.527 cm
Solenoid outer radius	4.406 cm

Max power deposited in beam pipe from uniform beam heating

If you assume a 1mA beam then the beam power incident on the target is

Beam Power = E(MeV) [math] \cdot [/math]I ([math]\mu[/math] A) = 10 MeV [math]\times[/math] 1000 mA = 10 kW

If the beam does not interact with the target and all the beam power is distributed uniformly along a 100 cm long beam pipe with a diameter of 3.48 cm then the power deposited per area would be

[math]10000 \mbox{W} \times \frac{1}{100 \mbox{cm}}\times \frac{1}{ \pi \times 3.48 \mbox {cm} } = 2.3 \frac{\mbox{W}}{\mbox{cm}^2}[/math]

A simulation predicts that about 8 out of 20 electrons will interact with the target and intercept a 34.8 mm diameter beam pipe surrounding the target.

[math]\mbox{P}_{\mbox{max}} = \left ( \frac{2}{5} \right ) 2.3 \frac{\mbox{W}}{\mbox{cm}^2}\lt 1 \frac{\mbox{W}}{\mbox{cm}^2}[/math]

BUT the beam does not intersect the pipe uniformly and instead can have a hot spot.

Heating along the Z-axis

GEANT4 predicts that scattered electrons, photons, and positrons (mostly scattered electrons) deposit

Energy deposited (MeV) in a 1 m long 3.48 cm diameter beam pipe surrounding a 2 mm target located at Z=-900 mm.

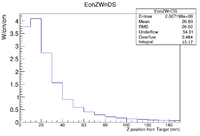
According to the above figure, GEANT4 predicts a total of [math]3.08\times 10^7[/math] MeV (the integral adds up the energy in each 1cm bin) of energy will be deposited in a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target. The peak energy deposition is 0.3 MeV/e[math]^-[/math]

If this energy were uniformly distributed along the 5 mm thick beam pipe having a diameter of 3.48 cm then I would see

[math]3.08 \times 10^{10} \mbox{keV} \times \frac{1}{100 \mbox{cm}}\times \frac{1}{ \pi \times 3.48 \mbox {cm} } \times \frac{1}{2 \times 10^7 \mbox{e}^-}=3.5\frac{\mbox{keV}}{\mbox{cm}^2 \;\;\mbox{e}^-}[/math]

if you assume a 1 mA beam of electrons then this becomes

[math]\left ( \frac{3.5 \; \mbox{W} }{ \mbox{cm}^2 } \right) [/math]

I converted the above histogram to deposited power by 1000 mA, divide by the number of incident electrons, divide by the circumference of the beam pipe, convert the number of electrons to Coulombs, and use a unit conversion from MeV to W-s per MeV.

[math]\left(Counts \frac{\mbox{MeV}}{\mbox{cm}}\right) \times \left( \frac{1}{2 \times 10^{7} \mbox{e}^-} \right ) \times \left( \frac{1}{ \pi \times 3.48 \mbox{cm}} \right ) \times \left( \frac{1. \times 10^{-3}\mbox{ C}}{\mbox{s} }\right )\times \left( \frac{\mbox{e}^- }{1.6 \times 10^{-19}\mbox{ C}}\right ) \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right ) \times [/math]

If you use the above factors to weight the histogram, then the figure below shows that GEANT4 predicts a power deposition density of [math]= 4 \frac{W}{cm^2}[/math], 1 cm downstream of the target. Back scattered electrons appear to create the hottest spot of [math]= 15 \frac{W}{cm^2}[/math] about 1cm upstream of the target.

Power Deposition Zoomed in and 902 mm offset applied	Power deposition over the 1 m long beam pipe

BeamPipeHeating_4mmthick_PbBi_PositronTarget

NiowaveTargetHeatingResult_2015

Unit conversion

The energy deposited by photon, electrons, and positrons is predicted by GEANT4 and recorded in energy units of keV per incident electron on the PbBi target. To convert this deposited energy to a power you need to assume a beam current. Assuming 1 beam current of 1 mA, the conversion is given easily as

[math]\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-16}\mbox{W} \cdot \mbox{ s}}{\mbox{keV} }\right )[/math]

[math]\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )[/math]

Results Table

Beam Pipe Diameter (mm)	Hot Spot ([math]MeV/e^-[/math])
34.8	0.35
47.5	0.24
60.2	0.20
72.9	0.16
97.4	0.12

G4Beamline_PbBi#Beam_Pipe_Heating