|
|
| Line 210: |
Line 210: |
| | | | |
| | {| class="wikitable" align="center" | | {| class="wikitable" align="center" |
| − | | style="background: gray" | <math>p^*_{2(z)}=-\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}</math> | + | | style="background: gray" | <math>p^*_{2(z)}=\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}</math> |
| | |} | | |} |
| | | | |
| − |
| |
| − | We choose negative, since the incoming electron in the lab frame is traveling in the positive direction, and the Moller electron is initially at rest, which translates to negative motion in the CM frame.
| |
| | | | |
| | | | |
Setup
Since we want to run for a evenly spaced energy range for Moller electrons, we will need to use some of the scattered electrons to help cover this range. A Moller scattering data file of 1E7 events has no Moller electrons with momentum over 5500 MeV. Since momentum is conserved, and the data is verified kinematicly verified, we can simply "switch" the data. This data can then be altered to have a certain number of different phi values for each energy to match the Moller cross section. This data can then be written to a LUND file, and compared to the previous calculations which did not factor in loss of initial energy.
Prepare Data
Using the existing Moller scattering data from a GEANT simulation of 4E7 incident electrons, a file of just scattered momentum components can be constructed using:
awk '{print $9, $10, $11, $16, $17, $18}' MollerScattering_NH3_Large.dat > Just_Scattered_Momentum.dat
Transfer to CM Frame
Center of Mass Frame
4-Momentum Invariants
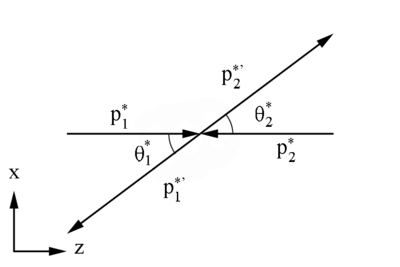 Figure 1: Definition of variables in the Center of Mass Frame
Figure 1: Definition of variables in the Center of Mass Frame
Starting with the definition for the total relativistic energy:
[math]E^2\equiv p^2c^2+m^2c^4[/math]
[math]\Longrightarrow {E^2}-p^2c^2=(mc^2)^2[/math]
Since we can assume that the frame of reference is an inertial frame, it moves at a constant velocity, the mass should remain constant.
[math]\frac {d\vec p}{dt}=0\Rightarrow \frac{d(m\vec v)}{dt}=\frac{c\ dm}{dt}\Rightarrow \frac{dm}{dt}=0[/math]
[math] \therefore m=const[/math]
We can use 4-momenta vectors, i.e. [math]{\mathbf P}\equiv \left(\begin{matrix} E\\ p_x \\ p_y \\ p_z \end{matrix} \right)=\left(\begin{matrix} E\\ \vec p \end{matrix} \right)[/math] ,with c=1, to describe the variables in the CM Frame.
Using the fact that the scalar product of a 4-momenta with itself,
[math]{\mathbf P_1}\cdot {\mathbf P^1}=P_{\mu}g_{\mu \nu}P^{\nu}=\left(\begin{matrix} E\\ p_x \\ p_y \\ p_z \end{matrix} \right)\cdot \left( \begin{matrix}1 & 0 & 0 & 0\\0 & -1 & 0 & 0\\0 & 0 & -1 & 0\\0 &0 & 0 &-1\end{matrix} \right)\cdot \left(\begin{matrix} E & p_x & p_y & p_z \end{matrix} \right)[/math]
[math]{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=s[/math]
is invariant.
Using this notation, the sum of two 4-momenta forms a 4-vector as well
[math]{\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\\vec p_1 +\vec p_2 \end{matrix} \right)= {\mathbf P}[/math]
The length of this four-vector is an invariant as well
[math]{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s[/math]
Equal masses
For incoming electrons moving only in the z-direction, we can write
[math]{\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)={\mathbf P}[/math]
We can perform a Lorentz transformation to the Center of Mass frame, with zero total momentum
[math]\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)[/math]
Without knowing the values for gamma or beta, we can utalize the fact that lengths of the two 4-momenta are invariant
[math]s={\mathbf P^*}^2=(E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2=(m_{1}^*+m_{2}^*)^2[/math]
[math]s={\mathbf P}^2=(E_{1}+E_{2})^2-(\vec p_{1}+\vec p_{2})^2=(m_{1}+m_{2})^2[/math]
This gives,
[math]\Longrightarrow (m_{1}^*+m_{2}^*)^2=(m_{1}+m_{2})^2[/math]
Using the fact that
[math]\begin{cases}
m_{1}=m_{2} \\
m_{1}^*=m_{2}^*
\end{cases}[/math]
since the rest mass energy of the electrons remains the same in inertial frames.
Substituting, we find
[math](m_{1}^*+m_{1}^*)^2=(m_{1}+m_{1})^2[/math]
[math]2m_{1}^*=2m_{1}[/math]
[math]m_{1}^*=m_{1}[/math]
[math]\Longrightarrow m_{1}=m^*_{1}\ ; m_{2}=m^*_{2}[/math]
This confirms that the mass remains constant between the frames of reference.
Total Energy in CM
Setting the lengths of the 4-momenta equal to each other,
[math]{\mathbf P^*}^2={\mathbf P}^{'2}[/math]
we can use this for the collision of two particles of mass m. Since the total momentum is zero in the Center of Mass frame, we can express total energy in the center of mass frame as
[math](E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2=s=(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2[/math]
[math](E^*)^2-(\vec p\ ^*)^2=(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2[/math]
[math](E^*)^2=(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2[/math]
[math]E^*=\sqrt{(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2}[/math]
[math]\left( \begin{matrix}E^*_{1}+E^*_{2}\\ p_{1(x)}^*+p_{2(x)}^* \\ p_{1(y)}^*+p_{2(y)}^* \\ p_{1(z)}^*+p_{2(z)}^*\end{matrix} \right)=\left(\begin{matrix}\gamma & 0 & 0 & -\beta \gamma\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta \gamma & 0 & 0 & \gamma \end{matrix} \right) . \left( \begin{matrix}E_{1}^'+E_{2}^'\\ p_{1(x)}^'+p_{2(x)}^' \\ p_{1(y)}^'+p_{2(y)}^' \\ p_{1(z)}^'+p_{2(z)}^'\end{matrix} \right)[/math]
[math]\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma & 0 & 0 & -\beta \gamma\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta \gamma & 0 & 0 & \gamma \end{matrix} \right) . \left( \begin{matrix}E^'\\ p_{x}^' \\ p_{y}^' \\ p_{z}^'\end{matrix} \right)[/math]
By the definition of the CM Frame we know
[math]\Longrightarrow\begin{cases}
E_2^*=\gamma(E_{2}^'+m)-\beta \gamma p_{2(z)}^' \\
p^*_{x}=p^'_{x}=0 \\
p^*_{y}=p^'_{y}=0 \\
p^*_{2(z)}=-\beta \gamma(E_{2}^'+m)+\gamma p_{2(z)}^'
\end{cases}[/math]
[math]\Longrightarrow \begin{cases}
p_{1(x)}^'=-p_{2(x)}^' \\
p_{1(y)}^'=-p_{2(y)}^'
\end{cases}[/math]
[math]\vec {p}\, ^*=\vec {p_1}^*+\vec {p_2}^*=0 \Longrightarrow \vec {p_1}^*=-\vec {p_2}^* [/math]
[math]E^*=\sqrt{(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2}[/math]
Using the relativistic definition of total energy:
[math]E^2 \equiv p^2+m^2[/math]
[math]E_1^*=\sqrt{p_1^{*2}+m^2}[/math]
[math]E_1^*=\sqrt{p_2^{*2}+m^2}=\sqrt{(-p_1)^{*2}+m^2}=\sqrt{p_1^{*2}+m^2}[/math]
[math]\therefore E^*=E_1^*+E_2^* \Longrightarrow E_1^*=E_2^*[/math]
Since the energies are equal, we use this fact to find the momenta
[math]|p_1^*|=|p_2^*|=\sqrt{E_1^{*2}-m^{*2}}[/math]
Moller electron Center of Mass Frame
Relativistically, the x and y components remain the same in the conversion from the Lab frame to the Center of Mass frame, since the direction of motion is only in the z direction.
| [math]p^*_{2(x)}\Leftrightarrow p_{2(x)}'[/math]
|
| [math]p^*_{2(y)}\Leftrightarrow p_{2(y)}'[/math]
|
| [math]p^*_{2(z)}=\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}[/math]
|
Redefining the components in simpler terms, we use the fact that
[math]E^*\equiv E^*_1+E^*_2[/math]
[math]2E^*_2=\sqrt{2m(m+E_1)}[/math]
| [math]E^*_2=\sqrt{\frac{m(m+E_1)}{2}}[/math]
|
| [math] p^*_{2}=\sqrt{E_{2}^{*2}-m^2}[/math]
|
Initially, before the collision in the CM frame, p2 was in the negative z direction. After the collision, the direction should reverse to the positive z direction. This same switching of the momentum direction alters p1 as well.
Using [math]\theta '_2=\arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right)[/math]
| [math]\Longrightarrow \theta ^*_2=\arccos \left(\frac{p^*_{2(z)}}{p^*_{2}}\right)[/math]
|
Determing Angles
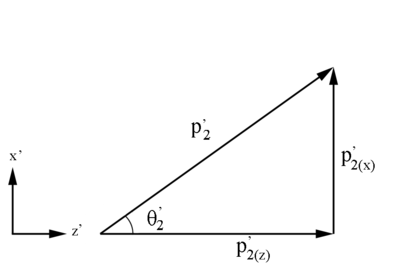 Figure 2: Definition of Moller electron variables in the Lab Frame in the x-z plane.
Figure 2: Definition of Moller electron variables in the Lab Frame in the x-z plane.
[math]\theta '_2\equiv \arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right)[/math]
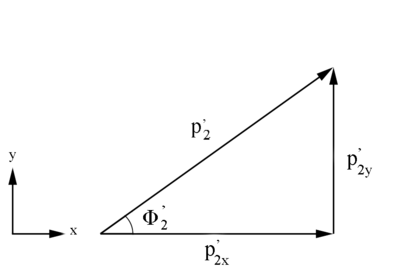 Figure 3: Definition of Moller electron variables in the Lab Frame in the x-y plane.
Figure 3: Definition of Moller electron variables in the Lab Frame in the x-y plane.
[math]\phi '_2\equiv \arccos \left( \frac{p^'_{2(x) Lab}}{p^'_{2(xy)}} \right)[/math]
where [math]p_{2(xy)}^'=\sqrt{(p_{2(x)}^')^2+(p^'_{2(y)})^2}[/math]
[math](p^'_{2(xy)})^2=(p^'_{2(x)})^2+(p^'_{2(y)})^2[/math]
and using [math]p^2=p_{(x)}^2+p_{(y)}^2+p_{(z)}^2[/math]
this gives [math](p^'_{2})^2=(p^'_{2(xy)})^2+(p^'_{2(z)})^2[/math]
[math]\Longrightarrow (p'_{2})^2-(p'_{2(z)})^2 = (p'_{2(xy)})^2[/math]
[math]\Longrightarrow p_{2(xy)}^'=\sqrt{(p^'_{2})^2-(p^'_{2(z)})^2}[/math]
which gives[math]\phi '_2 = \arccos \left( \frac{p_{2(x)}'}{\sqrt{p_{2}^{'\ 2}-p_{2(z)}^{'\ 2}}}\right)[/math]
| [math]\Longrightarrow p_{2(x)}'=\sqrt{p_{2}^{'\ 2}-p_{2(z)}^{'\ 2}} \cos(\phi)[/math]
|
Similarly, using [math]p_{2}^2=p_{2(x)}^2+p_{2(y)}^2+p_{2(z)}^2[/math]
[math]\Longrightarrow p_{2}^{'\ 2}-p_{2(x)}^{'\ 2}-p_{2(z)}^{'\ 2}=p_{2(y)}^{'\ 2}[/math]
| [math]p_{2(y)}'=\sqrt{p_{2}^{'\ 2}-p_{2(x)}^{'\ 2}-p_{2(z)}^{'\ 2}}[/math]
|
[math]p_{x}[/math] and [math]p_{y}[/math] results based on [math]\phi[/math]
Checking on the sign from the cosine results for [math]\phi '_2[/math]
We have the limiting range that [math]\phi[/math] must fall within:
| [math]-\pi \le \phi '_2 \le \pi\ Radians[/math]
|
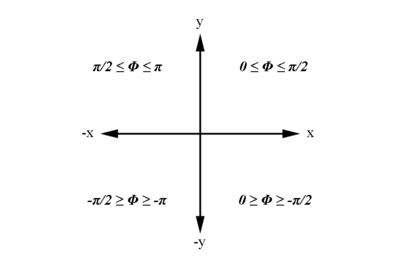
Examining the signs of the components which make up the angle [math]\phi[/math] in the 4 quadrants which make up the xy plane:
| [math]For\ 0 \ge \phi '_2 \ge \frac{-\pi}{2}\ Radians[/math]
|
| px=POSITIVE
|
| py=NEGATIVE
|
| [math]For\ 0 \le \phi '_2 \le \frac{\pi}{2}\ Radians[/math]
|
| px=POSITIVE
|
| py=POSITIVE
|
| [math]For\ \frac{-\pi}{2} \ge \phi '_2 \ge -\pi\ Radians[/math]
|
| px=NEGATIVE
|
| py=NEGATIVE
|
| [math]For\ \frac{\pi}{2} \le \phi '_2 \le \pi\ Radians[/math]
|
| px=NEGATIVE
|
| py=POSITIVE
|
Partial Check
Alter Phi Angles
Run for Necessary Amount to match Cross Section



