Reconstructing Moller Events

Setup

Since we want to run for a evenly spaced energy range for Moller electrons, we will need to use some of the scattered electrons to help cover this range. A Moller scattering data file of 1E7 events has no Moller electrons with momentum over 5500 MeV. Since momentum is conserved, and the data is verified kinematicly verified, we can simply "switch" the data. This data can then be altered to have a certain number of different phi values for each energy to match the Moller cross section. This data can then be written to a LUND file, and compared to the previous calculations which did not factor in loss of initial energy.

Prepare Data

Using the existing Moller scattering data from a GEANT simulation of 4E7 incident electrons, a file of just scattered momentum components can be constructed using:

awk '{print $9, $10, $11, $16, $17, $18}' MollerScattering_NH3_Large.dat > Just_Scattered_Momentum.dat

Transfer to CM Frame

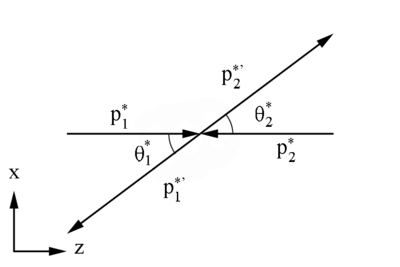
Center of Mass Frame

4-Momentum Invariants

Figure 2: Definition of variables in the Center of Mass Frame

Starting with the definition for the total relativistic energy:

[math]E^2\equiv p^2c^2+m^2c^4[/math]

[math]\Longrightarrow {E^2}-p^2c^2=(mc^2)^2[/math]

Since we can assume that the frame of reference is an inertial frame, it moves at a constant velocity, the mass should remain constant.

[math]\frac {d\vec p}{dt}=0\Rightarrow \frac{d(m\vec v)}{dt}=\frac{c\ dm}{dt}\Rightarrow \frac{dm}{dt}=0[/math]

[math] \therefore m=const[/math]

We can use 4-momenta vectors, i.e. [math]{\mathbf P}\equiv \left(\begin{matrix} E\\ p_x \\ p_y \\ p_z \end{matrix} \right)=\left(\begin{matrix} E\\ \vec p \end{matrix} \right)[/math] ,with c=1, to describe the variables in the CM Frame.

Using the fact that the scalar product of a 4-momenta with itself,

[math]{\mathbf P_1}\cdot {\mathbf P^1}=P_{\mu}g_{\mu \nu}P^{\nu}=\left(\begin{matrix} E\\ p_x \\ p_y \\ p_z \end{matrix} \right)\cdot \left( \begin{matrix}1 & 0 & 0 & 0\\0 & -1 & 0 & 0\\0 & 0 & -1 & 0\\0 &0 & 0 &-1\end{matrix} \right)\cdot \left(\begin{matrix} E & p_x & p_y & p_z \end{matrix} \right)[/math]

[math]{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=s[/math]

is invariant.

Using this notation, the sum of two 4-momenta forms a 4-vector as well

[math]{\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\\vec p_1 +\vec p_2 \end{matrix} \right)= {\mathbf P}[/math]

The length of this four-vector is an invariant as well

[math]{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s[/math]

Equal masses

For incoming electrons moving only in the z-direction, we can write

[math]{\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)={\mathbf P}[/math]

We can perform a Lorentz transformation to the Center of Mass frame, with zero total momentum

[math]\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)[/math]

Without knowing the values for gamma or beta, we can utalize the fact that lengths of the two 4-momenta are invariant

[math]s={\mathbf P^*}^2=(E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2=(m_{1}^*+m_{2}^*)^2[/math]

[math]s={\mathbf P}^2=(E_{1}+E_{2})^2-(\vec p_{1}+\vec p_{2})^2=(m_{1}+m_{2})^2[/math]

This gives,

[math]\Longrightarrow (m_{1}^*+m_{2}^*)^2=(m_{1}+m_{2})^2[/math]

Using the fact that

[math]\begin{cases} m_{1}=m_{2} \\ m_{1}^*=m_{2}^* \end{cases}[/math]

since the rest mass energy of the electrons remains the same in inertial frames.

Substituting, we find

[math](m_{1}^*+m_{1}^*)^2=(m_{1}+m_{1})^2[/math]

[math]2m_{1}^*=2m_{1}[/math]

[math]m_{1}^*=m_{1}[/math]

[math]\Longrightarrow m_{1}=m^*_{1}\ ; m_{2}=m^*_{2}[/math]

This confirms that the mass remains constant between the frames of reference.

Total Energy in CM

Setting the lengths of the 4-momenta equal to each other,

[math]{\mathbf P^*}^2={\mathbf P}^{'2}[/math]

we can use this for the collision of two particles of mass m. Since the total momentum is zero in the Center of Mass frame, we can express total energy in the center of mass frame as

[math](E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2=s=(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2[/math]

[math](E^*)^2-(\vec p\ ^*)^2=(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2[/math]

[math](E^*)^2=(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2[/math]

[math]E^*=\sqrt{(E_{1}^'+E_{2}^')^2-(\vec{p_{1}}^'+\vec {p_{2}}^')^2}[/math]

Scattered / Moller Electron energies and momenta in CM

By the definition of the CM Frame we know

[math]\vec {p}^*=\vec {p_1}^*+\vec {p_2}^*=0 \Longrightarrow \vec {p_1}^*=-\vec {p_2}^* [/math]

Using the relativistic definition of total energy:

[math]E^2 \equiv p^2+m^2[/math]

[math]E_1^*=\sqrt{p_1^{*2}+m^2}[/math]

[math]E_1^*=\sqrt{p_2^{*2}+m^2}=\sqrt{(-p_1)^{*2}+m^2}=\sqrt{p_1^{*2}+m^2}[/math]

[math]\therefore E^*=E_1^*+E_2^* \Longrightarrow E_1^*=E_2^*[/math]