|
|
| Line 203: |
Line 203: |
| | | | |
| | where it was already shown that since p<sub>z</sub> is the only cartesian component affected by the Lorentz shift | | where it was already shown that since p<sub>z</sub> is the only cartesian component affected by the Lorentz shift |
| − | <center><math>\frac{dE}{dp}=\frac{dE}{dp_z}=\frac{p_z}{E}=\frac{p}{E}\LongRightarrow \frac{dp}{dE}=\frac{E}{p}</math></center> | + | <center><math>\frac{dE}{dp}=\frac{dE}{dp_z}=\frac{p_z}{E}=\frac{p}{E}\Rightarrow \frac{dp}{dE}=\frac{E}{p}</math></center> |
| | | | |
| | | | |
| | Our final expression | | Our final expression |
| | <center><math>\frac{\partial ^2\sigma(E,\, \theta ,\, \phi)}{\partial E\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{\partial (p^*\,\cos{\theta^*)}}{\partial (E\,\cos{\theta})}</math></center> | | <center><math>\frac{\partial ^2\sigma(E,\, \theta ,\, \phi)}{\partial E\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{\partial (p^*\,\cos{\theta^*)}}{\partial (E\,\cos{\theta})}</math></center> |
Revision as of 19:18, 3 February 2016
Scattering Cross Section
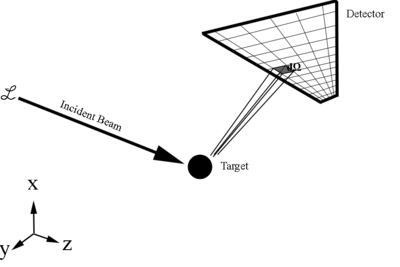
[math]\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
[math]\Rightarrow \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi =\frac{N}{\mathcal L}\equiv total\ scattering\ cross\ section[/math]
Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur.
Transforming Cross Section Between Frames
Cross Section as a Function of Momentum and Solid Angle
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames. This is due to the fact that
[math]\sigma=\frac{N}{\mathcal L}=constant\ number[/math]
This makes the total cross section a Lorentz invariant in that it is not effected by any relativistic transformations.
[math]\therefore\ \sigma_{CM}=\sigma_{Lab}[/math]
This implies that the number of particles going into the solid-angle element d ΩLab and having a momentum between pLab and pLab+dpLabbe the same as the number going into the corresponding solid-angle element dΩCM and having a corresponding momentum between pCM and pCM+dpCM
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega}dp \,d\Omega=\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^* \,\partial \Omega^* }dp^* \, d\Omega^*[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
Expressing this in terms of the solid angle components,
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega}\partial p \,\sin{\theta} \,d\theta \,d\phi=\frac{d^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{dp^* \, d\Omega^*}dp^*\, \sin{\theta^*}\,d\theta^* \,d\phi^*[/math]
As shown earlier,
[math]\phi=\phi^*[/math]
Thus,
[math]\Rightarrow\ d\phi=d\phi^*[/math]
Simplify our expression for the cross section gives:
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p \,\partial \Omega} dp \,\sin{\theta}\,d\theta=\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*}dp^*\, \sin{\theta^*}\,d\theta^*[/math]
We can use the fact that
[math]\sin{\theta}\ d\theta=d(\cos{\theta})[/math]
To give
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} dp\,d(\cos{\theta})=\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*}dp^*\, d(\cos{\theta^*})[/math]
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{dp^*\,d(\cos{\theta^*})}{dp\,d(\cos{\theta})}[/math]
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{\partial (p^*\,\cos{\theta^*)}}{\partial (p\,\cos{\theta})}[/math]
Using Chain Rule
We can use the chain rule to find the transformation term on the right hand side:
[math]\frac{\partial (p^*\, \cos{\theta^*)}}{\partial (p^*\, \theta^*\, \phi^*)} \frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)} \frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p_x\, p_y\, p_z)} \frac{\partial (p_x\, p_y\, p_z)}{\partial (p\, \theta\, \phi)} \frac{\partial (p\, \theta\, \phi)}{\partial (p\, \cos{\theta})}=\frac{\partial (p^*\, \cos{\theta^*})}{\partial (p\, \cos{\theta})}[/math]
Starting with the term:
[math]\frac{\partial (p^*\, \cos{\theta^*})} {\partial (p^*\, \theta^*\phi^*)}=\frac{d p^*\, \sin{\theta^*} \, d \theta^* \, d \phi^*}{d p^*\, d \theta^*\, d \phi^*}=\sin{\theta^*}[/math]
Similarly,
[math]\frac{\partial (p\, \theta\, \phi)}{\partial (p\, \cos{\theta})}=\frac{1}{\sin{\theta}}[/math]
Using the conversion of cartesian to spherical coordinates we know:
[math]\begin{cases}
p_x=p\, \sin{\theta}\, \cos{\phi} \\
p_y=p\, \sin{\theta}\, \sin{\phi} \\
p_z=p\, \cos{\theta}
\end{cases}[/math]
and the fact that as was shown earlier, that
[math]\begin{cases}
p^*_x=p_x \\
p^*_y=p_y \\
\phi^*=\phi
\end{cases}[/math]
This allows us to express the term:
[math]\frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)}=\biggl[\frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p^*\, \theta^*\, \phi^*)}\biggr]^{-1}=\biggl[\frac{\partial (p^*\, \sin{\theta^*}\, \cos{\phi^*}p^*\, \sin{\theta^*}\, \sin{\phi^*}p^*\, \cos{\theta^*})}{\partial p^*\, \partial \theta^*\, \partial \phi^*}\biggr]^{-1}[/math]
[math]\frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)}=\biggl[ \frac{d (p^{*-1})\, d(\cos{\theta^{*}}^{-1})} {d p^*\, d\theta^*}\biggr]=\frac{1}{p^{*2}\sin{\theta^*}}[/math]
Again, similarly
[math]\frac{\partial (p_x\, p_y\, p_z)}{\partial (p\, \theta\, \phi)}=p^2\, \sin{\theta}[/math]
To find the middle component in the chain rule expansion,
[math]\left( \begin{matrix} E^* \\ p^*_x \\ p^*_y \\ p^*_z\end{matrix} \right)=\left(\begin{matrix}\gamma & 0 & 0 & -\beta \gamma\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta\gamma & 0 & 0 & \gamma \end{matrix} \right) . \left( \begin{matrix}E\\ p_x \\ p_y\\ p_z\end{matrix} \right)[/math]
which gives,
[math]\Longrightarrow\begin{cases}
E^*=\gamma E-\beta \gamma^* p_z \\
p^*_z=-\beta \gamma\, E+\gamma\, p_z
\end{cases}[/math]
[math]\frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p_x\, p_y\, p_z)}=\frac{\partial p^*_z}{\partial p_z}=\frac{\partial (-\beta \gamma\, E+\gamma\, p_z)}{\partial p_z}=-\beta \gamma \,\frac{\partial E}{\partial p_z}+\gamma[/math]
We can use the relativistic definition of the total Energy,
[math]E=\sqrt{p^2+m^2}=\sqrt{p_x^2+p_y^2+p_z^2+m^2}[/math]
[math]\Rightarrow \frac{\partial E}{\partial p_z}=\frac{\sqrt {p_x^2+p_y^2+p_z^2+m^2}} {\partial p_z}=\frac{p_z}{\sqrt {p_x^2+p_y^2+p_z^2+m^2}}=\frac{p_z}{E}[/math]
[math]\frac{\partial p^*_z}{\partial p_z}=-\beta \gamma \frac{\partial E}{\partial p_z}+\gamma=-\beta \gamma \frac{p_z}{E}+\gamma[/math]
Then using the fact that
[math]E^*\equiv \gamma E-\beta \gamma\, p_z [/math]
[math]\frac{\partial p^*_z}{\partial p_z}=-\beta \gamma \frac{p_z}{E}+\frac{\gamma\, E}{E}=\frac{E^*}{E}[/math]
Final Expression
Using the values found above, our expression becomes:
[math]\frac{\partial (p^*\, \cos{\theta^*)}}{\partial (p^*\, \theta^*\, \phi^*)} \frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)} \frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p_x\, p_y\, p_z)} \frac{\partial (p_x\, p_y\, p_z)}{\partial (p\, \theta\, \phi)} \frac{\partial (p\, \theta\, \phi)}{\partial (p\, \cos{\theta})}=\frac{\partial (p^*\, \cos{\theta^*})}{\partial (p\, \cos{\theta})}[/math]
This gives,
[math][/math]
| [math]\Longrightarrow \frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{p^2E^*}{p^{*2}E}[/math]
|
Cross Section as a Function of Energy, Momentum, and Solid Angle
[math]\frac{\partial ^2\sigma(E,\, \theta ,\, \phi)}{\partial E\,\partial \Omega} dp\,d(\cos{\theta})=\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*}dp^*\, d(\cos{\theta^*})[/math]
[math]\frac{\partial ^2\sigma(E,\, \theta ,\, \phi)}{\partial E\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{dp^*\,d(\cos{\theta^*})}{dE\,d(\cos{\theta})}[/math]
[math]\frac{\partial ^2\sigma(E,\, \theta ,\, \phi)}{\partial E\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{\partial (p^*\,\cos{\theta^*)}}{\partial (E\,\cos{\theta})}[/math]
We can use the chain rule to find the transformation term on the right hand side:
[math]\frac{\partial (p^*\, \cos{\theta^*)}}{\partial (p\, \cos{\theta})} \frac{\partial (p\, \cos{\theta})}{\partial (E\, \cos{\theta})}=\frac{\partial (p^*\, \cos{\theta^*})}{\partial (E\, \cos{\theta})}[/math]
Using the expression found earlier,
[math]\frac{\partial (p^*\, \cos{\theta^*)}}{\partial (p\, \cos{\theta})}=\frac{p^2E^*}{p^{*2}E}[/math]
This gives,
[math]\frac{p^2E^*}{p^{*2}E} \frac{\partial (p\, \cos{\theta})}{\partial (E\, \cos{\theta})}=\frac{p^2E^*}{p^{*2}E} \frac{dp\, d(\cos{\theta})}{dE\, d(\cos{\theta})}=\frac{p^2E^*}{p^{*2}E} \frac{dp}{dE}[/math]
where it was already shown that since pz is the only cartesian component affected by the Lorentz shift
[math]\frac{dE}{dp}=\frac{dE}{dp_z}=\frac{p_z}{E}=\frac{p}{E}\Rightarrow \frac{dp}{dE}=\frac{E}{p}[/math]
Our final expression
[math]\frac{\partial ^2\sigma(E,\, \theta ,\, \phi)}{\partial E\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{\partial (p^*\,\cos{\theta^*)}}{\partial (E\,\cos{\theta})}[/math]
