|
|
| Line 22: |
Line 22: |
| | which can be expanded to | | which can be expanded to |
| | | | |
| − | <center><math>{\mathbf P^*}^2={\mathbf P}^2={\mathbf P^'}^2</math></center> | + | <center><math>{\mathbf P^*}^2={\mathbf P^{'*}}^2={\mathbf P}^2={\mathbf P^'}^2</math></center> |
| | | | |
| | | | |
| | <center>''where'' <math>{\mathbf P^'}=({\mathbf P_1^'}+{\mathbf P_2^'})^2</math> ''represents the 4-Momentum Vector in the final Lab frame''</center> | | <center>''where'' <math>{\mathbf P^'}=({\mathbf P_1^'}+{\mathbf P_2^'})^2</math> ''represents the 4-Momentum Vector in the final Lab frame''</center> |
| | + | |
| | + | |
| | + | <center>''and'' <math>{\mathbf P^{'*}}=({\mathbf P_1^{'*}}+{\mathbf P_2^{'*}})^2</math> ''represents the 4-Momentum Vector in the final CM frame''</center> |
| | | | |
| | ==New 4-Momentum Quantities== | | ==New 4-Momentum Quantities== |
Revision as of 23:21, 31 January 2016
Lorentz Invariant Quantities
Total 4-Momentums
As was shown earlier the scalar product of a 4-Momentum vector with itself ,
[math]{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=s[/math] ,
and the length of a 4-Momentum vector composed of 4-Momentum vectors,
[math]{\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=(m_1+m_2)^2=s[/math],
are invariant quantities.
It was further shown that
[math]{\mathbf P^*}^2={\mathbf P}^2[/math]
where [math]{\mathbf P^*}=({\mathbf P_1^*}+{\mathbf P_2^*})^2[/math] represents the 4-Momentum Vector in the CM frame
and [math]{\mathbf P}=({\mathbf P_1}+{\mathbf P_2})^2[/math] represents the 4-Momentum Vector in the initial Lab frame
which can be expanded to
[math]{\mathbf P^*}^2={\mathbf P^{'*}}^2={\mathbf P}^2={\mathbf P^'}^2[/math]
where [math]{\mathbf P^'}=({\mathbf P_1^'}+{\mathbf P_2^'})^2[/math] represents the 4-Momentum Vector in the final Lab frame
and [math]{\mathbf P^{'*}}=({\mathbf P_1^{'*}}+{\mathbf P_2^{'*}})^2[/math] represents the 4-Momentum Vector in the final CM frame
New 4-Momentum Quantities
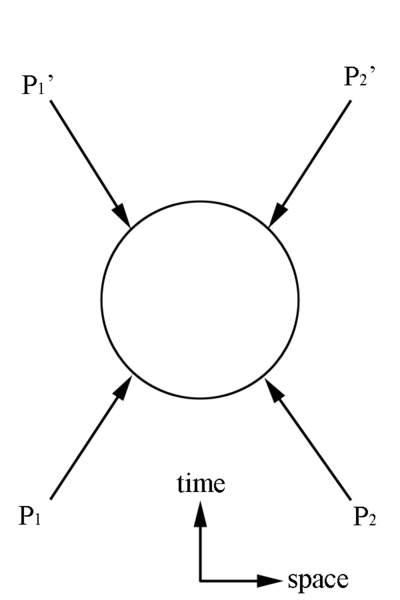
Working in just the Lab frame, we can form new 4-Momentum Vectors comprised of 4-Momenta in this frame, with
[math]{\mathbf P_1}- {\mathbf P_1^'}= \left( \begin{matrix}E_1-E_1'\\ p_{1(x)}-p_{1(x)}^' \\ p_{1(y)}-p_{1(y)}^' \\ p_{1(z)}-p_{1(z)}^'\end{matrix} \right)={\mathbf P_a}[/math]
[math]{\mathbf P_1}- {\mathbf P_2^'}= \left( \begin{matrix}E_1-E_2'\\ p_{1(x)}-p_{2(x)}^' \\ p_{1(y)}-p_{2(y)}^' \\ p_{1(z)}-p_{2(z)}^'\end{matrix} \right)={\mathbf P_b}[/math]
[math]{\mathbf P_2}- {\mathbf P_1^'}= \left( \begin{matrix}E_2-E_1'\\ p_{2(x)}-p_{1(x)}^' \\ p_{2(y)}-p_{1(y)}^' \\ p_{2(z)}-p_{1(z)}^'\end{matrix} \right)={\mathbf P_c}[/math]
[math]{\mathbf P_2}- {\mathbf P_2^'}= \left( \begin{matrix}E_2-E_2'\\ p_{2(x)}-p_{2(x)}^' \\ p_{2(y)}-p_{2(y)}^' \\ p_{2(z)}-p_{2(z)}^'\end{matrix} \right)={\mathbf P_d}[/math]
Using the algebraic fact
[math]\left({\mathbf a}- {\mathbf b}\right)^2=\left({\mathbf b}- {\mathbf a}\right)^2[/math]
and the fact that the length of these 4-Momentum Vectors are invariant,
[math]\left({\mathbf P_1}- {\mathbf P_1^'}\right)^2=\left({\mathbf P_1}^2-2{\mathbf P_1}\cdot {\mathbf P_1^'}+ {\mathbf P_1^'}\right)= \left( \begin{matrix}E_1-E_1'\\ p_{1(x)}-p_{1(x)}^' \\ p_{1(y)}-p_{1(y)}^' \\ p_{1(z)}-p_{1(z)}^'\end{matrix} \right)^2=\left({\mathbf P_a}\right)^2=s[/math]
[math]\left({\mathbf P_1}- {\mathbf P_2^'}\right)^2=\left({\mathbf P_1}^2-2{\mathbf P_1}\cdot {\mathbf P_2^'}+ {\mathbf P_2^'}\right)= \left( \begin{matrix}E_1-E_2'\\ p_{1(x)}-p_{2(x)}^' \\ p_{1(y)}-p_{2(y)}^' \\ p_{1(z)}-p_{2(z)}^'\end{matrix} \right)^2=\left({\mathbf P_b}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_1^'}\right)^2=\left({\mathbf P_2}^2-2{\mathbf P_2}\cdot {\mathbf P_1^'}+ {\mathbf P_1^'}\right)= \left( \begin{matrix}E_2-E_1'\\ p_{2(x)}-p_{1(x)}^' \\ p_{2(y)}-p_{1(y)}^' \\ p_{2(z)}-p_{1(z)}^'\end{matrix} \right)^2=\left({\mathbf P_c}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_2^'}\right)^2=\left({\mathbf P_2}^2-2{\mathbf P_2}\cdot {\mathbf P_2^'}+ {\mathbf P_2^'}\right)= \left( \begin{matrix}E_2-E_2'\\ p_{2(x)}-p_{2(x)}^' \\ p_{2(y)}-p_{2(y)}^' \\ p_{2(z)}-p_{2(z)}^'\end{matrix} \right)^2=\left({\mathbf P_d}\right)^2=s[/math]
Using the fact that the scalar product of a 4-momenta with itself is invariant,
[math]{\mathbf P_1}\cdot {\mathbf P^1}=E_1E_1-\vec p_1\cdot \vec p_1 =m_{1}^2=s[/math]
We can simiplify the expressions
[math]\left({\mathbf P_1}- {\mathbf P_1^'}\right)^2=\left( m_1^2-2{\mathbf P_1}\cdot {\mathbf P_1^'}+ m_1^{'2}\right)=\left({\mathbf P_a}\right)^2=s[/math]
[math]\left({\mathbf P_1}- {\mathbf P_2^'}\right)^2=\left( m_1^2-2{\mathbf P_1}\cdot {\mathbf P_2^'}+ m_2^{'2}\right)=\left({\mathbf P_b}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_1^'}\right)^2=\left( m_2^2-2{\mathbf P_2}\cdot {\mathbf P_1^'}+ m_1^{'2}\right)=\left({\mathbf P_c}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_2^'}\right)^2=\left( m_2^2-2{\mathbf P_2}\cdot {\mathbf P_2^'}+ m_2^{'2}\right)=\left({\mathbf P_d}\right)^2=s[/math]
Finding the cross terms,
[math]{\mathbf P_1}\cdot {\mathbf P^'}=\left(\begin{matrix} E\\ p_x \\ p_y \\ p_z \end{matrix} \right)\cdot \left( \begin{matrix}1 & 0 & 0 & 0\\0 & -1 & 0 & 0\\0 & 0 & -1 & 0\\0 &0 & 0 &-1\end{matrix} \right)\cdot \left(\begin{matrix} E' & p_x^' & p_y^' & p_z^' \end{matrix} \right)=E_1E_1^'-\vec p_1\cdot \vec p_1^' [/math]
This gives
[math]\left({\mathbf P_1}- {\mathbf P_1^'}\right)^2=\left( m_1^2-2\left(E_1E_1^'-\vec p_1\cdot \vec p_1^'\right)+ m_1^{'2}\right)=\left({\mathbf P_a}\right)^2=s[/math]
[math]\left({\mathbf P_1}- {\mathbf P_2^'}\right)^2=\left( m_1^2-2\left(E_1E_2^'-\vec p_1\cdot \vec p_2^'\right)+ m_2^{'2}\right)=\left({\mathbf P_b}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_1^'}\right)^2=\left( m_2^2-2\left(E_2E_1^'-\vec p_2\cdot \vec p_1^'\right)+ m_1^{'2}\right)=\left({\mathbf P_c}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_2^'}\right)^2=\left( m_2^2-2\left(E_2E_2^'-\vec p_2\cdot \vec p_2^'\right)+ m_2^{'2}\right)=\left({\mathbf P_d}\right)^2=s[/math]
Using the fact that energy is conserved in this elastic collision
[math]\left({\mathbf P_1}- {\mathbf P_1^'}\right)^2=\left( m_1^2-2\left((E-E_2)(E-E_2^')-\vec p_1\cdot \vec p_1^'\right)+ m_1^{'2}\right)=\left({\mathbf P_a}\right)^2=s[/math]
[math]\left({\mathbf P_1}- {\mathbf P_2^'}\right)^2=\left( m_1^2-2\left((E-E_2)(E-E_1^')-\vec p_1\cdot \vec p_2^'\right)+ m_2^{'2}\right)=\left({\mathbf P_b}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_1^'}\right)^2=\left( m_2^2-2\left((E-E_1)(E-E_2^')-\vec p_2\cdot \vec p_1^'\right)+ m_1^{'2}\right)=\left({\mathbf P_c}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_2^'}\right)^2=\left( m_2^2-2\left((E-E_1)(E-E_1^')-\vec p_2\cdot \vec p_2^'\right)+ m_2^{'2}\right)=\left({\mathbf P_d}\right)^2=s[/math]
[math]\left({\mathbf P_1}- {\mathbf P_1^'}\right)^2=\left( m_1^2-2\left((E^2-EE_2-EE_2^'+E_2E_2^')-\vec p_1\cdot \vec p_1^'\right)+ m_1^{'2}\right)=\left({\mathbf P_a}\right)^2=s[/math]
[math]\left({\mathbf P_1}- {\mathbf P_2^'}\right)^2=\left( m_1^2-2\left((E^2-EE_2-EE_1^'+E_2E_1^')-\vec p_1\cdot \vec p_2^'\right)+ m_2^{'2}\right)=\left({\mathbf P_b}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_1^'}\right)^2=\left( m_2^2-2\left((E^2-EE_1-EE_2^'+E_1E_2^')-\vec p_2\cdot \vec p_1^'\right)+ m_1^{'2}\right)=\left({\mathbf P_c}\right)^2=s[/math]
[math]\left({\mathbf P_2}- {\mathbf P_2^'}\right)^2=\left( m_2^2-2\left((E^2-EE_1-EE_1^'+E_1E_1^')-\vec p_2\cdot \vec p_2^'\right)+ m_2^{'2}\right)=\left({\mathbf P_d}\right)^2=s[/math]
Mandelstam Representation