DV Calculations of 4-momentum components

Calculations of 4-momentum components

Initial Conditions

Lab Frame

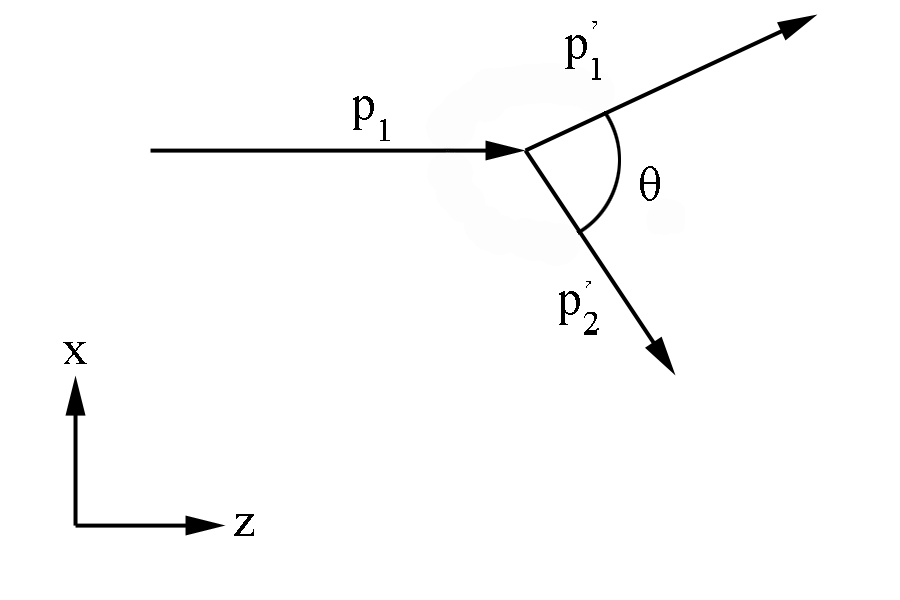Figure 1: Definition of variables in the Lab Frame

Begining with the assumption that the incoming electron, p₁, has momentum of 11000 MeV in the positive z direction.

$\vec p_{1(z)}\equiv \vec p_{1}=11000 MeV \widehat {z}$

We can also assume the Moller electron, p₂, is initially at rest

$\vec p_{2}\equiv 0$

This gives the total energy in this frame as

$E\equiv \sqrt{p^2+m^2}$

$E\equiv \sqrt{(p_{1}+p_{2})^2+(m_{1}+m_{2})^2}$

$\Longrightarrow E\equiv \sqrt{(11000 MeV)^2+(.511 MeV+.511 MeV)^2}\approx 11000 MeV$

Center of Mass Frame

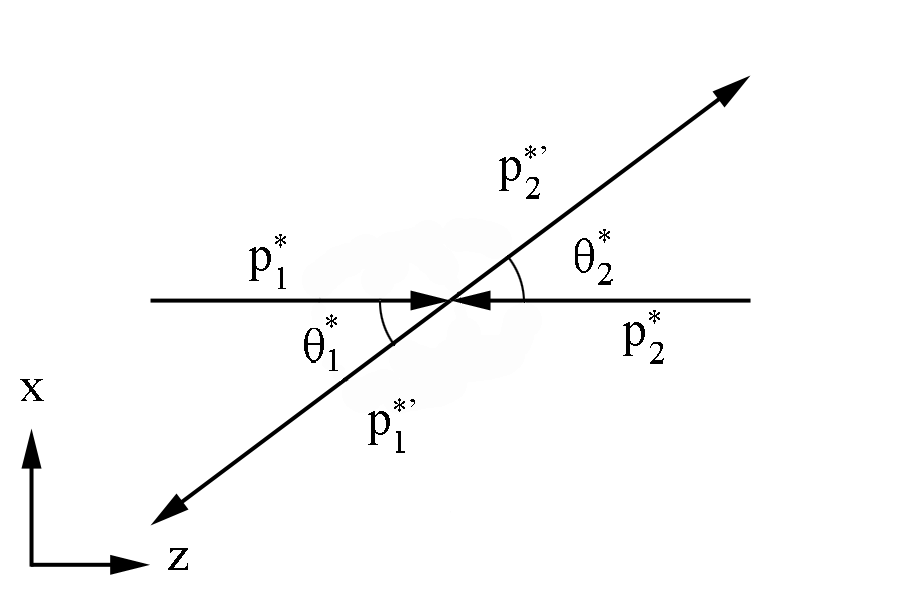Figure 2: Definition of variables in the Center of Mass Frame

Starting with the definition for the total relativistic energy:

$E^2\equiv p^2c^2+m^2c^4$

$\Longrightarrow \frac {E^2}{c^2}-p^2=m^2 c^2$

We can use 4-momenta vectors, i.e. ${\mathbf P}\equiv \left(\begin{matrix} E/c\\ p_x \\ p_y \\ p_z \end{matrix} \right)$ , to describe the variables in the CM Frame.

Using this notation, the sum of two 4-momenta forms a 4-vector as well

${\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\\vec p_1 c+\vec p_2 c\end{matrix} \right)= {\mathbf P}$

We can perform a Lorentz transformation to the Center of Mass frame, with zero total momentum

$\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)$

Without knowing the values for gamma or beta, we can show that lengths of the two 4-momenta are invariant

$s={\mathbf P^*}^2=(E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2=(m_{1}^*+m_{2}^*)^2$

$s={\mathbf P}^2=(E_{1}+E_{2})^2-(\vec p_{1}+\vec p_{2})^2=(m_{1}+m_{2})^2$

$\Longrightarrow (m_{1}^*+m_{2}^*)^2=(m_{1}+m_{2})^2$

Using the fact that

$\begin{cases} m_{1}=m_{2} \\ m_{1}^*=m_{2}^* \end{cases}$

$(m_{1}^*+m_{1}^*)^2=(m_{1}+m_{1})^2$

$2m_{1}^*=2m_{1}$

$m_{1}^*=m_{1}$

$\Longrightarrow m_{1}=m^*_{1}\ ; m_{2}=m^*_{2}$

and using the fact that the scalar product of a 4-momenta with itself,

${\mathbf P_1}\cdot {\mathbf P_1}=E_1E_1-\vec p_1\cdot \vec p_1 c^2=m_1^2c^4=s$

is invariant

The length of this four-vector is an invariant as well

${\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 c+\vec p_2 c)^2=(m_1c^4+m_2c^4)^2=s$

${\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=s$ (with c=1)

For incoming electrons moving only in the z-direction, we can write

${\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)={\mathbf P}$

Setting these equal to each other, we can use this for the collision of two particles of mass m₁ and m₂. Since the total momentum is zero in the Center of Mass frame, we can express total energy in the center of mass frame as

$(E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2=s=(E_{1}+E_{2})^2-(\vec{p_{1}}+\vec p_{2})^2$

$(E^*)^2-(\vec p\ ^*)^2=(E_{1}+E_{2})^2-(\vec{p_{1}}+\vec p_{2})^2$

$(E^*)^2=(E_{1}+E_{2})^2-(\vec{p_{1}}+\vec p_{2})^2$

$E^*=[(E_{1}+E_{2})^2-(\vec{p_{1}}+\vec p_{2})^2]^{1/2}$

$E^*=[E_{1}^2+2E_{1}E_{2}+E_{2}^2-\vec p_{1} . \vec p_{2} -\vec p_{1} . \vec p_{1} -\vec p_{2} . \vec p_{1} -\vec p_{2} . \vec p_{2} ]^{1/2}$

$E^*=[(E_{1}^2- p_{1}^2 )+(E_{2}^2-p_{2}^2 )+2E_{1}E_{2}-\vec p_{1} . \vec p_{2} -\vec p_{2} . \vec p_{1} ]^{1/2}$

$E^*=[(E_{1}^2- p_{1}^2 )+(E_{2}^2-p_{2}^2 )+2E_{1}E_{2}-p_{1} p_{2}\cos(\theta) - p_{2} p_{1}\cos(\theta) ]^{1/2}$

$E^*=[m_{1}^2+m_{2}^2+2E_{1}E_{2}-p_{1} p_{2}\cos(\theta) - p_{2} p_{1}\cos(\theta) ]^{1/2}$

$E^*=[m_{1}^2+m_{2}^2+2E_{1}E_{2}-2p_{1} p_{2}\cos(\theta) ]^{1/2}$

$E^*=[m_{1}^2+m_{2}^2+2E_{1}E_{2}-2p_{1} p_{2}\cos(\theta) ]^{1/2}$

Using the relations $\beta\equiv \vec p/E\Longrightarrow \vec p=\beta E$

$E^*=[m_{1}^2+m_{2}^2+2E_{1}E_{2}(1-\beta_{1}\beta_{2}\cos(\theta))]^{1/2}$

where $\theta$ is the angle between the particles in the Lab frame.

In the frame where one particle (m₂) is at rest

$\Longrightarrow \beta_{2}=0$

$\Longrightarrow p_{2}=0$

which implies,

$E_{2}=[p_{2}^2+m_{2}^2]^{1/2}=m_{2}$

$E^*=(m_{1}^2+m_{2}^2+2E_{1} m_{2})^{1/2}=(.511MeV^2+.511MeV^2+2(\sqrt{(11000 MeV)^2+(.511 MeV)^2})(.511 MeV))^{1/2}\approx 106.030760886 MeV$

where $E_{1}=\sqrt{p_{1}^2+m_{1}^2}\approx 11000 MeV$

Inspecting the Lorentz transformation to the Center of Mass frame:

$\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ 0 \\ 0 \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)$

For the case of a stationary electron, this simplifies to:

$\left( \begin{matrix} E^* \\ p^*_{x} \\ p^*_{y} \\ p^*_{z}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+m_{2}\\ 0 \\ 0 \\ p_{1(z)}+0\end{matrix} \right)$

which gives,

$\Longrightarrow\begin{cases} E^*=\gamma^* (E_{1}+m_{2})-\beta^* \gamma^* p_{1(z)} \\ p^*_{z}=-\beta^* \gamma^*(E_{1}+m_{2})+\gamma^* p^*_{1(z)} \end{cases}$

Solving for $\beta^*$, with $p^*_{z}=0$

$\Longrightarrow \beta^* \gamma^*(E_{1}+m_{2})=\gamma^* p_{1(z)}$

$\Longrightarrow \beta^*=\frac{p_{1}}{(E_{1}+m_{2})}$

Similarly, solving for $\gamma^*$ by substituting in $\beta^*$

$E^*=\gamma^* (E_{1}+m_{2})-\frac{p_{1}}{(E_{1}+m_{2})} \gamma^* p_{1(z)}$

$E^*=\gamma^* \frac{(E_{1}+m_2)^2}{(E_{1}+m_{2})}-\gamma^*\frac{(p_{1(z)})^2}{(E_{1}+m_{2})}$

Using the fact that $E^*=[(E_{1}+E_{2})^2-(\vec p_{1}+\vec p_{2})^2]^{1/2}$

$E^*=\gamma^* \frac{E^*\ ^2}{(E_{1}+m_{2})}$

$\Longrightarrow \gamma^*=\frac{(E_1+m_2)} {E^*}$

Using the relation

$\left( \begin{matrix} E^*_{1}+E^*_{2} \\ p^*_{1(x)}+p^*_{2(x)} \\ p^*_{1(y)}+p^*_{2(y)} \\ p^*_{1(z)}+p^*_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+m_{2}\\ 0 \\ 0 \\ p_{1(z)}+0\end{matrix} \right)$

$\Longrightarrow \left( \begin{matrix} E^*_{2} \\ p^*_{2(x)} \\ p^*_{2(y)} \\ p^*_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}m\\ 0 \\ 0 \\ 0\end{matrix} \right)$

$\Longrightarrow\begin{cases} E^*_{2}=\gamma^* (m_{2}) \\ p^*_{2(z)}=-\beta^* \gamma^* (m_{2}) \end{cases}$

$\Longrightarrow\begin{cases} E^*_{2}=\frac{(E_{1}+m_{2})}{E^*} (m_2) \\ p^*_{2(z)}=-\frac{p_{1}}{(E_{1}+m_2)} \frac{(E_{1}+m_{2})}{E^*} (m_{2}) \end{cases}$

$\Longrightarrow\begin{cases} E^*_{2}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (.511 MeV) \approx 53.0129177 MeV\\ p^*_{2(z)}=-\frac{11000 MeV}{106.031 MeV} (.511 MeV) \approx -53.013 MeV \end{cases}$

$\Longrightarrow \left( \begin{matrix} E^*_{1}\\ p^*_{1(x)} \\ p^*_{1(y)} \\ p^*_{1(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}\\ 0 \\ 0 \\ p_{1(z)}\end{matrix} \right)$

$\Longrightarrow\begin{cases} E^*_{1}=\gamma^* (E_{1})-\beta^* \gamma^* p_{1(z)} \\ p^*_{1(z)}=-\beta^* \gamma^*(E_{1})+\gamma^* p_{1(z)} \end{cases}$

$\Longrightarrow\begin{cases} E^*_{1}=\frac{(E_{1}+m_{2})}{E^*} (E_{1})-\frac{p_{1(z)}}{(E_{1}+m_2)} \frac{(E_{1}+m_{2})}{E^*} p_{1(z)} \\ p^*_{1(z)}=-\frac{p_{1}}{(E_{1}+m_2)} \frac{(E_{1}+m_{2})}{E^*}(E_{1})+\frac{(E_{1}+m_{2})}{E^*} p_{1(z)} \end{cases}$

$\Longrightarrow\begin{cases} E^*_{1}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (11000 MeV)-\frac{11000 MeV}{106.031 MeV} 11000 MeV \approx 53.013 MeV\\ p^*_{1(z)}=-\frac{11000 MeV}{106.031 MeV}(11000 MeV)+\frac{(11000 MeV+.511 MeV)}{106.031 MeV} 11000 MeV \approx 53.013 MeV \end{cases}$

$p^*_{1} =\sqrt {(p^*_{1(x)})^2+(p^*_{1(y)})^2+(p^*_{1(z)})^2} \Longrightarrow p^*_{1}=p^*_{1(z)}$

$p^*_{2} =\sqrt {(p^*_{2(x)})^2+(p^*_{2(y)})^2+(p^*_{2(z)})^2} \Longrightarrow p^*_{2}=p^*_{2(z)}$

This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions.

$p^*_{1}=p^*_{2}\approx 53.013 MeV$

$E^*_{1}= E^*_{2}\approx 53.013 MeV$

Final Conditions

Moller electron Lab Frame

Finding the correct kinematic values starting from knowing the momentum of the Moller electron, $p^'_{2}$ , in the Lab frame,

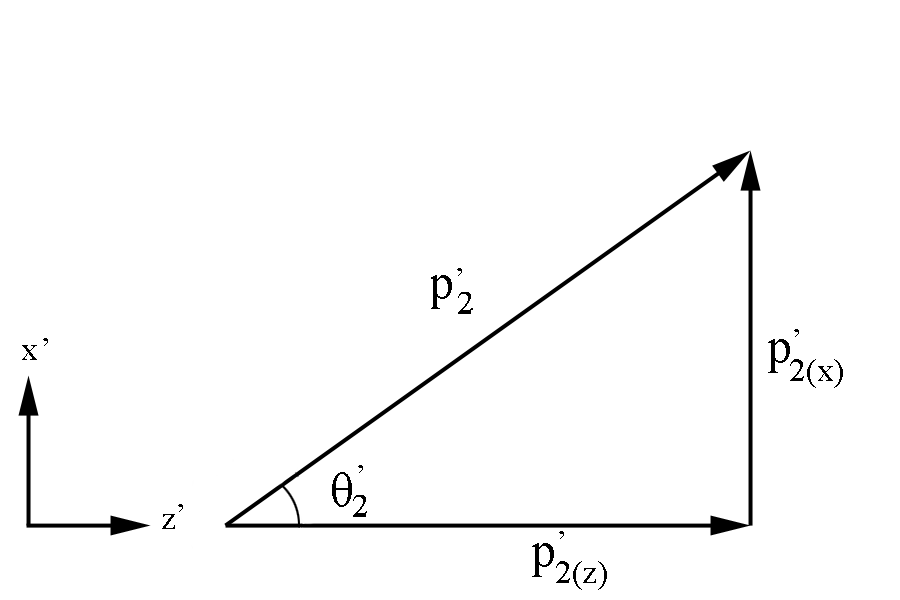Figure 3: Definition of Moller electron variables in the Lab Frame in the x-z plane. Using $\theta '_2=\arccos \left(\frac{p^'_{2(z)}}{p^'_{2}}\right)$

$\Longrightarrow {p^'_{2(z)}=p^'_{2}\cos(\theta '_2)}$

^'

Checking on the sign resulting from the cosine function, we are limited to:

$0^\circ \le \theta '_2 \le 60^\circ \equiv 0 \le \theta '_2 \le 1.046\ Radians$

Since,

$\frac{p^'_{2(z)}}{p^'_{2}}=cos(\theta '_2)$

$\Longrightarrow p^'_{2(z)}\ should\ always\ be\ positive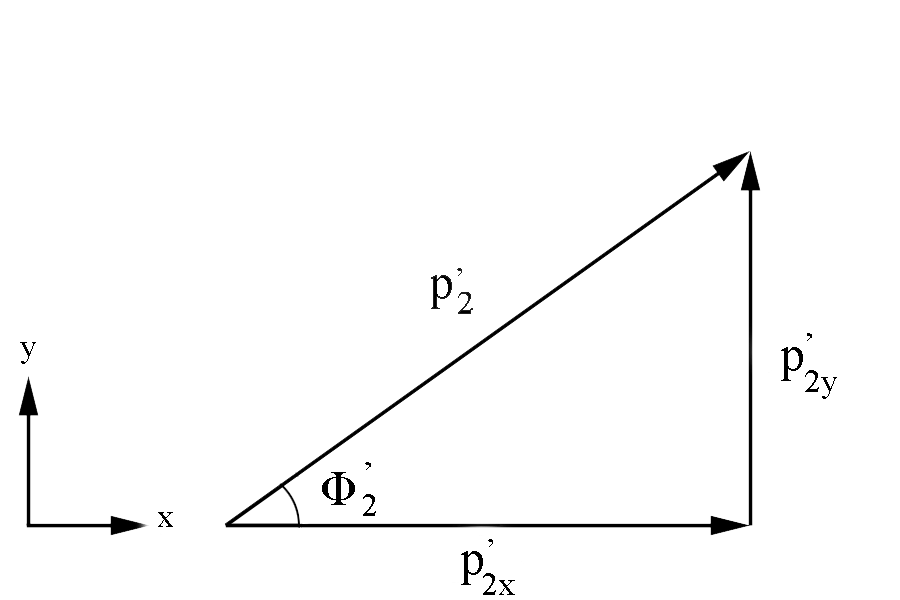$ Figure 4: Definition of Moller electron variables in the Lab Frame in the x-y plane. Similarly, $\phi '_2=\arccos \left( \frac{p^'_{2(x) Lab}}{p^'_{2(xy)}} \right)$

where $p_{2(xy)}^'=\sqrt{(p_{2(x)}^')^2+(p^'_{2(y)})^2}$

$(p^'_{2(xy)})^2=(p^'_{2(x)})^2+(p^'_{2(y)})^2$

and using $p^2=p_{(x)}^2+p_{(y)}^2+p_{(z)}^2$

this gives $(p^'_{2})^2=(p^'_{2(xy)})^2+(p^'_{2(z)})^2$

$\Longrightarrow (p'_{2})^2-(p'_{2(z)})^2 = (p'_{2(xy)})^2$

$\Longrightarrow p_{2(xy)}^'=\sqrt{(p^'_{2})^2-(p^'_{2(z)})^2}$

which gives$\phi '_2 = \arccos \left( \frac{p_{2(x)}'}{\sqrt{p_{2}^{'\ 2}-p_{2(z)}^{'\ 2}}}\right)$

$\Longrightarrow p_{2(x)}'=\sqrt{p_{2}^{'\ 2}-p_{2(z)}^{'\ 2}} \cos(\phi)$

Similarly, using $p_{2}^2=p_{2(x)}^2+p_{2(y)}^2+p_{2(z)}^2$

$\Longrightarrow p_{2}^{'\ 2}-p_{2(x)}^{'\ 2}-p_{2(z)}^{'\ 2}=p_{2(y)}^{'\ 2}$

$p_{2(y)}'=\sqrt{p_{2}^{'\ 2}-p_{2(x)}^{'\ 2}-p_{2(z)}^{'\ 2}}$

Checking on the sign from the cosine results for $\phi '_2$

$-\pi \le \phi '_2 \le \pi\ Radians$

$For\ 0 \le \phi '_2 \le \frac{-\pi}{2}\ Radians$

x=POSITIVE

y=NEGATIVE

$For\ 0 \le \phi '_2 \le \frac{\pi}{2}\ Radians$

x=POSITIVE

y=POSITIVE

$For\ \frac{-\pi}{2} \le \phi '_2 \le -\pi\ Radians$

x=NEGATIVE

y=NEGATIVE

$For\ \frac{\pi}{2} \le \phi '_2 \le \pi\ Radians$

x=NEGATIVE

y=POSITIVE

Moller electron Center of Mass Frame

Relativistically, the x and y components remain the same in the conversion from the Lab frame to the Center of Mass frame, since the direction of motion is only in the z direction.

$p^*_{2(x)}\Leftrightarrow p_{2(x)}'$

$p^*_{2(y)}\Leftrightarrow p_{2(y)}'$

$p^*_{2(z)}=\sqrt {(p^*_2)^2-(p^*_{2(x)})^2-(p^*_{2(y)})^2}$

$\Longrightarrow E^*_{2}=\approx 53.013 MeV$

Electron Center of Mass Frame

Relativistically, the x, y, and z components have the same magnitude, but opposite direction, in the conversion from the Moller electron's Center of Mass frame to the electron's Center of Mass frame.

$p^*_{2(x)}= -p^*_{1(x)}$

$p^*_{2(y)}= -p^*_{1(y)}$

$p^*_{2(z)}=-p^*_{1(z)}$

where previously it was shown

$p^*_{1}\approx 53.013 MeV$

$E^*_{1}\approx 53.013 MeV$

Electron Lab Frame

We can perform a Lorentz transformation from the Center of Mass frame, with zero total momentum, to the Lab frame.

$\left( \begin{matrix}E'_{1}+E'_{2}\\ p'_{1(x)}+p'_{2(x)} \\p'_{1(y)}+ p'_{2(y)} \\ p'_{1(z)}+p'_{2(z)}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & \beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ \beta^* \gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E^*_{1}+E^*_{2}\\ p^*_{1(x)}+p^*_{2(x)} \\ p^*_{(1(y)}+p^*_{2(y)} \\ p^*_{1(z)}+p^*_{2(z)}\end{matrix} \right)$

$p^*_{1(x)}= p'_{1(x)}$

$p^*_{1(y)}= p'_{1(y)}$

$\Longrightarrow\begin{cases} E'=\gamma E^*+\beta \gamma p^*_{z} \\ p'_{z}=\beta \gamma E^*+ \gamma p^*_{z} \end{cases}$

$\Longrightarrow\begin{cases} \gamma = \frac{E'}{E^*} \\ \beta =\frac{p'_{z}}{E'} \end{cases}$

Without knowing the values for gamma or beta, we can use the fact that lengths of the two 4-momenta are invariant

$s={\mathbf P^*} ^2=(E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2$

$s={\mathbf P}^2=(E'_{1}+E'_{2})^2-(\vec p\ '_{1}+\vec p\ '_{2})^2$

Setting these equal to each other, we can use this for the collision of two particles of mass m₁ and m₂. Since the total momentum is zero in the Center of Mass frame, we can express total energy in the center of mass frame as

$(E^*_{1}+E^*_{2})^2-(\vec p\ ^*_{1}+\vec p\ ^*_{2})^2=s=(E'_{1}+E'_{2})^2-(\vec p\ '_{1}+\vec p\ '_{2})^2$

$(E^*)^2-(\vec p\ ^*)^2=(E'_{1}+E'_{2})^2-(\vec p\ ')^2$

$(E^*)^2=(E')^2-(\vec p\ ')^2$

$(E^*)^2+(\vec{p'})^2=(E')^2$

$E'=\sqrt{(E^*)^2+(\vec p\ ')^2}$

Since momentum is conserved, the initial momentum from the incident electron and stationary electron is still the same in the Lab frame, therefore $p\ '_{Lab}=11000 MeV$

$E'=\sqrt{(106.031 MeV)^2+(11000 MeV)^2}\approx 11000.511 MeV$

This is the same as the initial total energy in the Lab frame, which should be expected since scattering is considered to be an elastic collision.

Since,

$E'\equiv E'_{1}+E'_{2}$

$\Longrightarrow E'_{1}=E'-E'_{2}$

Using the relation

$E'^2\equiv p^2+m^2$

$\Longrightarrow p_{1}^{'\ 2}=E_{1}^{'\ 2}-m_{1}^2=E_{1}^{'\ 2}-(.511 MeV)^2$

Using

$p^2 \equiv p_x^2+p_y^2+p_z^2$

$\Longrightarrow p_{1(z)}'=\sqrt {p_{1}^{'\ 2}-p_{1(x)}^{'\ 2}-p_{1(y)}^{'\ 2}}$

DV_RunGroupC_Moller#Momentum distributions in the Center of Mass Frame

DV_MollerTrackRecon#Calculations_of_4-momentum_components