DV Calculations of 4-momentum components

Calculations of 4-momentum components

Initial Lab Frame

Assume the incoming electron has momentum of 11000 MeV in the positive z direction.

$p_{1\ z}\equiv p_{1}=11000 MeV$

The moller electron is initially at rest

$p_{2}\equiv 0$

The total energy in this frame

$E\equiv \sqrt{p^2+m^2}$

$E\equiv \sqrt{(p_{1}+p_{2})^2+(m_{1}+m_{2})^2}$

$\Longrightarrow E\equiv \sqrt{(11000 MeV)^2+(.511 MeV+.511 MeV)^2}\approx 11000 MeV$

Center of Mass Frame

Using the definition

$E^2\equiv p^2c^2+m^2c^4$

$\Longrightarrow p^2=\frac {E^2}{c^2}-m^2 c^2$

We can use 4-momenta vectors, i.e. ${\mathbf P}\equiv \left(\begin{matrix} E/c\\ p_x \\ p_y \\ p_z \end{matrix} \right)$

we can use the fact that the scalar product of a 4-momenta with itself,

${\mathbf P_1}\cdot {\mathbf P_1}=E_1E_1-\vec p_1\cdot \vec p_1 c^2=m_1^2c^4=s$

is invariant

Using this, the sum of two 4-momenta forms a 4-vector as well

${\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\\vec p_1 c+\vec p_2 c\end{matrix} \right)= {\mathbf P}$

The length of this four-vector is an invariant as well

${\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 c+\vec p_2 c)^2=(m_1c^4+m_2c^4)^2=s$

${\mathbf P^2}=({\mathbf P_1}+{\mathbf P_2})^2=(E_1+E_2)^2-(\vec p_1 +\vec p_2 )^2=s$ (with c=1)

For incoming electrons moving only in the z-direction, we can write

${\mathbf P_1}+ {\mathbf P_2}= \left( \begin{matrix}E_1+E_2\\ 0 \\ 0 \\ p_{1z}+p_{2z}\end{matrix} \right)={\mathbf P}$

We can perform a Lorentz transformation to the Center of Mass frame, with zero total momentum

$\left( \begin{matrix}E^*_{1}+E^*_{2}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma_{CM} & 0 & 0 & -\beta_{CM} \gamma_{CM}\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta_{CM} \gamma_{CM} & 0 & 0 & \gamma_{CM} \end{matrix} \right) . \left( \begin{matrix}E_{1 Lab}+E_{2 Lab}\\ 0 \\ 0 \\ p_{1z Lab}+p_{2z Lab}\end{matrix} \right)$

Without knowing the values for gamma or beta, we can use the fact that lengths of the two 4-momenta are invariant

$s={\mathbf P}_{CM}^2=(E_{1 CM}+E_{2 CM})^2-(\vec p_{1 CM}+\vec p_{2 CM})^2$

$s={\mathbf P}_{Lab}^2=(E_{1 Lab}+E_{2 Lab})^2-(\vec p_{1 Lab}+\vec p_{2 Lab})^2$

$\Longrightarrow m_{1 Lab}=m_{1 CM}\ ; m_{2 Lab}=m_{2 CM}$

Setting these equal to each other, we can use this for the collision of two particles of mass m₁ and m₂. Since the total momentum is zero in the Center of Mass frame, we can express total energy in the center of mass frame as

$(E_{1 CM}+E_{2 CM})^2-(\vec p_{1 CM}+\vec p_{2 CM})^2=s=(E_{1 Lab}+E_{2 Lab})^2-(\vec{p_{1 Lab}}+\vec p_{2 Lab})^2$

$(E_{CM})^2-(\vec p_{CM})^2=(E_{1 Lab}+E_{2 Lab})^2-(\vec{p_{1 Lab}}+\vec p_{2 Lab})^2$

$(E_{CM})^2=(E_{1 Lab}+E_{2 Lab})^2-(\vec{p_{1 Lab}}+\vec p_{2 Lab})^2$

$E_{CM}=[(E_{1 Lab}+E_{2 Lab})^2-(\vec{p_{1 Lab}}+\vec p_{2 Lab})^2]^{1/2}$

$E_{CM}=[E_{1 Lab}^2+2E_{1 Lab}E_{2 Lab}+E_{2 Lab}^2-\vec p_{1 Lab} . \vec p_{2 Lab} -\vec p_{1 Lab} . \vec p_{1 Lab} -\vec p_{2 Lab} . \vec p_{1 Lab} -\vec p_{2 Lab} . \vec p_{2 Lab} ]^{1/2}$

$E_{CM}=[(E_{1 Lab}^2- p_{1 Lab}^2 )+(E_{2 Lab}^2-p_{2 Lab}^2 )+2E_{1 Lab}E_{2 Lab}-\vec p_{1 Lab} . \vec p_{2 Lab} -\vec p_{2 Lab} . \vec p_{1 Lab} ]^{1/2}$

$E_{CM}=[(E_{1 Lab}^2- p_{1 Lab}^2 )+(E_{2 Lab}^2-p_{2 Lab}^2 )+2E_{1 Lab}E_{2 Lab}-p_{1 Lab} p_{2 Lab}\cos(\theta_{Lab}) - p_{2 Lab} p_{1 Lab}\cos(\theta_{Lab}) ]^{1/2}$

$E_{CM}=[m_{1 Lab}^2+m_{2 Lab}^2+2E_{1 Lab}E_{2 Lab}-p_{1 Lab} p_{2 Lab}\cos(\theta_{Lab}) - p_{2 Lab} p_{1 Lab}\cos(\theta_{Lab}) ]^{1/2}$

$E_{CM}=[m_{1 Lab}^2+m_{2 Lab}^2+2E_{1 Lab}E_{2 Lab}-2p_{1 Lab} p_{2 Lab}\cos(\theta_{Lab}) ]^{1/2}$

$E_{CM}=[m_{1 Lab}^2+m_{2 Lab}^2+2E_{1 Lab}E_{2 Lab}-2p_{1 Lab} p_{2 Lab}\cos(\theta_{Lab}) ]^{1/2}$

Using the relations $\beta\equiv \vec p/E\Longrightarrow \vec p_{Lab}=\beta_{Lab} E_{Lab}$

$E_{CM}=[m_{1 Lab}^2+m_{2 Lab}^2+2E_{1 Lab}E_{Lab}2(1-\beta_{1 Lab}\beta_{2 Lab}\cos(\theta_{Lab}))]^{1/2}$

where $θ_{Lab}$ is the angle between the particles in the Lab frame.

$E_{CM}=[m_1^2+m_2^2+2E_{1 Lab}E_{2 Lab}(1-\beta_{1 Lab}\beta_{2 Lab}\cos(\theta_{Lab}))]^{1/2}$

In the frame where one particle (m_{2 Lab}) is at rest

$\Longrightarrow \beta_{2 Lab}=0$

$\Longrightarrow p_{2 Lab}=0$

which implies,

$E_{2 Lab}=[p_{2 Lab}^2+m_{2 Lab}^2]^{1/2}=m_{2 Lab}$

$E_{CM}=(m_{1 Lab}^2+m_{2 Lab}^2+2E_{1 Lab} m_{2 Lab})^{1/2}=(.511MeV^2+.511MeV^2+2(\sqrt{(11000 MeV)^2+(.511 MeV)^2})(.511 MeV))^{1/2}\approx 106.030760886 MeV$

where $E_{1 Lab}=\sqrt{p_{1 Lab}^2+m_{1 Lab}^2}\approx 11000 MeV$

Inspecting the Lorentz transformation to the Center of Mass frame:

$\left( \begin{matrix}E_{1 CM}+E_{2 CM}\\ 0 \\ 0 \\ 0\end{matrix} \right)=\left(\begin{matrix}\gamma_{CM} & 0 & 0 & -\beta_{CM} \gamma_{CM}\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta_{CM} \gamma_{CM} & 0 & 0 & \gamma_{CM} \end{matrix} \right) . \left( \begin{matrix}E_{1 Lab}+E_{2 Lab}\\ 0 \\ 0 \\ p_{1z Lab}+p_{2z Lab}\end{matrix} \right)$

For the case of a stationary electron, this simplifies to:

$\left( \begin{matrix} E_{CM} \\ p_{xCM} \\ p_{y CM} \\ p_{z CM}\end{matrix} \right)=\left(\begin{matrix}\gamma_{CM} & 0 & 0 & -\beta_{CM} \gamma\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta_{CM} \gamma_{CM} & 0 & 0 & \gamma_{CM} \end{matrix} \right) . \left( \begin{matrix}E_{1 Lab}+m_{2Lab}\\ 0 \\ 0 \\ p_{1z Lab}+0\end{matrix} \right)$

which gives,

$\Longrightarrow\begin{cases} E_{CM}=\gamma_{CM} (E_{1 Lab}+m_{2 Lab})-\beta_{CM} \gamma_{CM} p_{1z Lab} \\ p_{zCM}=-\beta_{CM} \gamma_{CM}(E_{1 Lab}+m_{2 Lab})+\gamma_{CM} p_{1z Lab} \end{cases}$

Solving for $\beta_{CM}$, with $p_{zCM}=0$

$\Longrightarrow \beta_{CM} \gamma_{CM}(E_{1 Lab}+m_{2 Lab})=\gamma_{CM} p_{1z Lab}$

$\Longrightarrow \beta_{CM}=\frac{p_{1 Lab}}{(E_{1 Lab}+m_{2 Lab})}$

Similarly, solving for $\gamma_{CM}$ by substituting in $\beta_{CM}$

$E_{CM}=\gamma_{CM} (E_{1 Lab}+m_{2 Lab})-\frac{p_{1 Lab}}{(E_{1 Lab}+m_{2 Lab})} \gamma_{CM} p_{1z Lab}$

$E_{CM}=\gamma_{CM} \frac{(E_{1 Lab}+m_2)^2}{(E_{1 Lab}+m_{2 Lab})}-\gamma_{CM}\frac{(p_{1z Lab})^2}{(E_{1 Lab}+m_{2 Lab})}$

Using the fact that $E_{CM}=[(E_{1 Lab}+E_{2 Lab})^2-(\vec p_{1 Lab}+\vec p_{2 Lab})^2]^{1/2}$

$E_{CM}=\gamma_{CM} \frac{E_{CM}^2}{(E_{1 Lab}+m_{2 Lab})}$

$\Longrightarrow \gamma_{CM}=\frac{(E_{1 Lab}+m_{2 Lab})}{E_{CM}}$

This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions

Using the relation

$\left( \begin{matrix} E_{1 CM}+E_{2 CM} \\ p_{1xCM}+p_{2xCM} \\ p_{1y CM}+p_{2yCM} \\ p_{1z CM}+p_{2zCM}\end{matrix} \right)=\left(\begin{matrix}\gamma_{CM} & 0 & 0 & -\beta_{CM} \gamma_{CM}\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta_{CM} \gamma_{CM} & 0 & 0 & \gamma_{CM} \end{matrix} \right) . \left( \begin{matrix}E_{1 Lab}+m_{2 Lab}\\ 0 \\ 0 \\ p_{1z Lab}+0\end{matrix} \right)$

$\Longrightarrow \left( \begin{matrix} E_{2 CM} \\ p_{2xCM} \\ p_{2yCM} \\ p_{2zCM}\end{matrix} \right)=\left(\begin{matrix}\gamma_{CM} & 0 & 0 & -\beta_{CM} \gamma_{CM}\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta_{CM} \gamma_{CM} & 0 & 0 & \gamma_{CM} \end{matrix} \right) . \left( \begin{matrix}m\\ 0 \\ 0 \\ 0\end{matrix} \right)$

$\Longrightarrow\begin{cases} E_{2CM}=\gamma_{CM} (m_{2 lab}) \\ p_{2zCM}=-\beta_{CM} \gamma_{CM} (m_{2 Lab}) \end{cases}$

$\Longrightarrow\begin{cases} E_{2CM}=\frac{(E_{1 Lab}+m_{2 Lab})}{E_{CM}} (m_2) \\ p_{2zCM}=-\frac{p_{1 Lab}}{(E_{1 Lab}+m_2)} \frac{(E_{1 Lab}+m_{2 Lab})}{E_{CM}} (m_{2 Lab}) \end{cases}$

$\Longrightarrow\begin{cases} E_{2CM}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (.511 MeV) \approx 53.0129177 MeV\\ p_{2zCM}=-\frac{11000 MeV}{106.031 MeV} (.511 MeV) \approx -53.013 MeV \end{cases}$

$\Longrightarrow \left( \begin{matrix} E_{1 CM}\\ p_{1xCM} \\ p_{1y CM} \\ p_{1z CM}\end{matrix} \right)=\left(\begin{matrix}\gamma_{CM} & 0 & 0 & -\beta_{CM} \gamma_{CM}\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta_{CM} \gamma_{CM} & 0 & 0 & \gamma_{CM} \end{matrix} \right) . \left( \begin{matrix}E_{1 Lab}\\ 0 \\ 0 \\ p_{1z Lab}\end{matrix} \right)$

$\Longrightarrow\begin{cases} E_{1CM}=\gamma_{CM} (E_{1 Lab})-\beta_{CM} \gamma_{CM} p_{1z Lab} \\ p_{1zCM}=-\beta_{CM} \gamma(E_{1 Lab})+\gamma_{CM} p_{1z Lab} \end{cases}$

$\Longrightarrow\begin{cases} E_{1CM}=\frac{(E_{1 Lab}+m_{2 Lab})}{E_{CM}} (E_{1 Lab})-\frac{p_{1zLab}}{(E_{1 Lab}+m_2)} \frac{(E_{1 Lab}+m_{2 Lab})}{E_{CM}} p_{1z Lab} \\ p_{1zCM}=-\frac{p_{1 Lab}}{(E_{1 Lab}+m_2)} \frac{(E_{1 Lab}+m_{2 Lab})}{E_{CM}}(E_{1 Lab})+\frac{(E_{1 Lab}+m_{2 Lab})}{E_{CM}} p_{1z Lab} \end{cases}$

$\Longrightarrow\begin{cases} E_{1CM}=\frac{(11000 MeV+.511 MeV)}{106.031 MeV} (11000 MeV)-\frac{11000 MeV}{106.031 MeV} 11000 MeV \approx 53.013 MeV\\ p_{1zCM}=-\frac{11000 MeV}{106.031 MeV}(11000 MeV)+\frac{(11000 MeV+.511 MeV)}{106.031 MeV} 11000 MeV \approx 53.013 MeV \end{cases}$

$p_{1 CM} =\sqrt{p_{1xCM}^2+p_{1yCM}^2+p_{1zCM}^2}\Longrightarrow p_{1 CM}=p_{1zCM}$

$p_{2 CM} =\sqrt{p_{2xCM}^2+p_{2yCM}^2+p_{2zCM}^2}\Longrightarrow p_{2 CM}=p_{2zCM}$

$p_{1 CM}=p_{2 CM}\approx 53.013 MeV$

$E_{1 CM}= E_{2 CM}\approx 53.013 MeV$

Moller electron Lab Frame

Finding the correct kinematic values starting from knowing the momentum of the Moller electron, $'''p_{(m)'''Lab}$ , in the Lab frame,

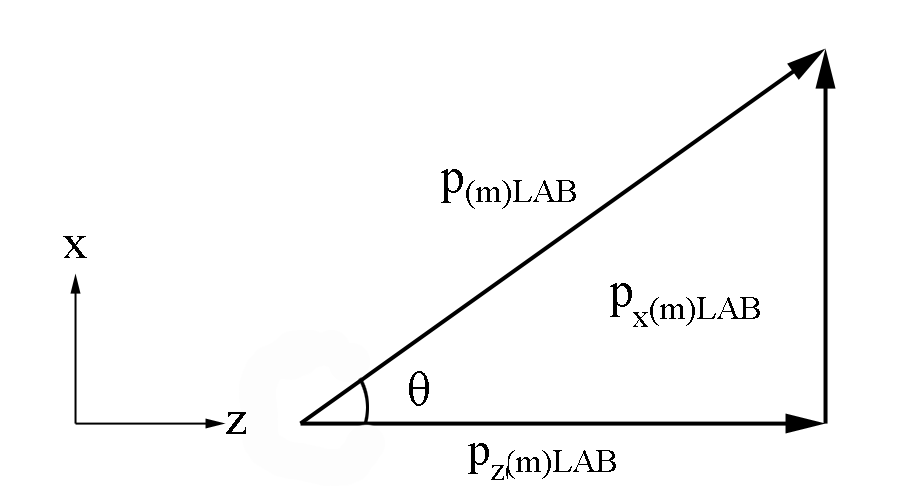Using $\theta=\arccos \left(\frac{p_{z(m) Lab}}{p_{(m)Lab}}\right)$

$\Longrightarrow {p_{z(m) Lab}=p_{(m)Lab}\cos(\theta)}$

Checking on the sign resulting from the cosine function, we are limited to:

$0^\circ \le \theta \le 60^\circ \equiv 0 \le \theta \le 1.046\ Radians$

Since,

$\frac{p_{(m)zLab}}{p_{(m)Lab}}=cos(\theta)$

$\Longrightarrow p_{(m)zLab}\ should\ always\ be\ positive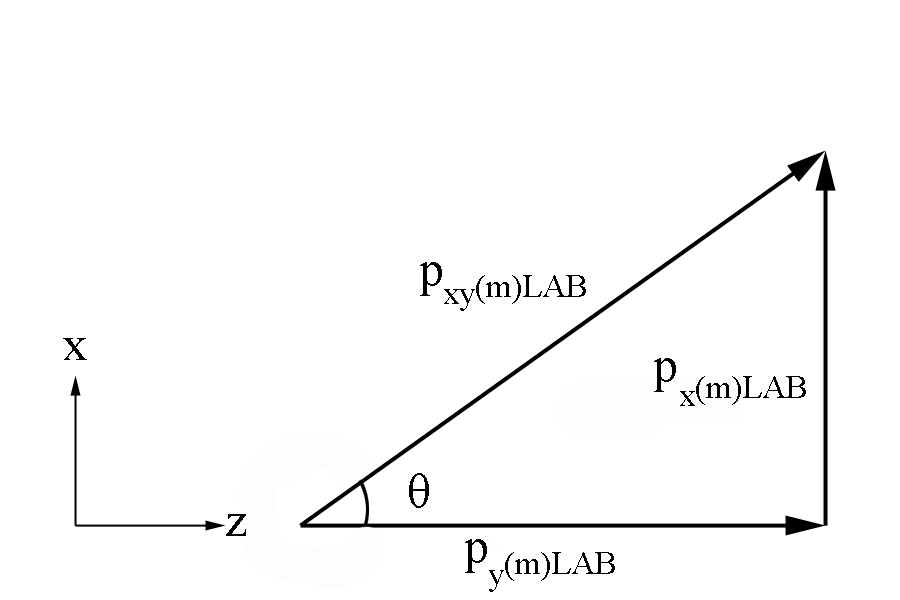$ Similarly, $\phi=\arccos \left( \frac{p_{x(m) Lab}}{p_{xy(m) Lab}} \right)$

where $p_{xy(m) Lab}=\sqrt{p_{x(m) Lab}^2+p_{y(m)Lab}^2}$

$p_{xy(m) Lab}=(p_{x(m) Lab}^2+p_{y(m) Lab}^2)^2$

and using $p_{(m)Lab}^2=p_{x(m) Lab}^2+p_{y(m) Lab}^2+p_{z(m) Lab}^2$

this gives $p_{(m)Lab}^2=p_{xy(m) Lab}^2+p_{z(m) Lab}^2$

$\Longrightarrow p_{(m)Lab}^2-p_{z(m) Lab}^2=p_{xy(m) Lab}^2$

$\Longrightarrow p_{xy(m) Lab}=\sqrt{p_{(m)Lab}^2-p_{z(m) Lab}^2}$

which gives$\phi = \arccos \left( \frac{p_{x(m) Lab}}{\sqrt{p_{(m)Lab}^2-p_{z(m) Lab}^2}}\right)$

$\Longrightarrow p_{x(m) Lab}=\sqrt{p_{(m)Lab}^2-p_{z(m) Lab}^2} \cos(\phi)$

Similarly, using $p_{(m)Lab}^2=p_{x(m) Lab}^2+p_{y(m) Lab}^2+p_{z(m) Lab}^2$

$\Longrightarrow p_{(m)Lab}^2-p_{x(m) Lab}^2-p_{z(m) Lab}^2=p_{y(m) Lab}^2$

$p_{y(m) Lab}=\sqrt{p_{(m)Lab}^2-p_{x(m) Lab}^2-p_{z(m) Lab}^2}$

Checking on the sign from the cosine results for $\phi$

$-\pi \le \phi \le \pi\ Radians$

$For\ 0 \le \phi \le \frac{-\pi}{2}\ Radians$

x=POSITIVE

y=NEGATIVE

$For\ 0 \le \phi \le \frac{\pi}{2}\ Radians$

x=POSITIVE

y=POSITIVE

$For\ \frac{-\pi}{2} \le \phi \le -\pi\ Radians$

x=NEGATIVE

y=NEGATIVE

$For\ \frac{\pi}{2} \le \phi \le \pi\ Radians$

x=NEGATIVE

y=POSITIVE

Moller electron Center of Mass Frame

Relativistically, the x and y components remain the same in the conversion from the Lab frame to the Center of Mass frame, since the direction of motion is only in the z direction.

$p_{x(m) CM}\Leftrightarrow p_{x(m) Lab}$

$p_{y(m) CM}\Leftrightarrow p_{y(m) Lab}$

$p_{z(m) CM}=\sqrt{p_{(m)CM}^2-p_{x(m) CM}^2-p_{y(m) CM}^2}$

$\Longrightarrow E_{(m) CM}=\sqrt{\frac{m(m+E_{(e^-) Lab})}{2}}$

Electron Center of Mass Frame

Relativistically, the x, y, and z components have the same magnitude, but opposite direction, in the conversion from the Moller electron's Center of Mass frame to the electron's Center of Mass frame.

$p_{x(m) CM}= -p_{x(e^-) CM}$

$p_{y(m) CM}= -p_{y((e^-) CM}$

$p_{z(m) CM}=-p_{z((e^-) CM}$

where previously it was shown

$p_{(e^-) CM}\approx 53.013 MeV$

$E_{(e^-) CM}\approx 53.013 MeV$

Electron Lab Frame

We can perform a Lorentz transformation from the Center of Mass frame, with zero total momentum, to the Lab frame.

$\left( \begin{matrix}E_{(e^-) Lab}+E_{(m) Lab}\\ p_{(e^-)z Lab}+p_{(m)z Lab} \\p_{(e^-)z Lab}+ p_{(m)z Lab} \\ p_{(e^-)z Lab}+p_{(m)z Lab}\end{matrix} \right)=\left(\begin{matrix}\gamma_{CM} & 0 & 0 & \beta_{CM} \gamma_{CM}\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ \beta_{CM} \gamma_{CM} & 0 & 0 & \gamma_{CM} \end{matrix} \right) . \left( \begin{matrix}E_{(e^-) CM}+E_{(m) CM}\\ p_{(e^-)x CM}+p_{(m)x CM} \\ p_{(e^-)y CM}+p_{(m)y CM} \\ p_{(e^-)z CM}+p_{(m)z CM}\end{matrix} \right)$

$p_{x(e^-) CM}= p_{x(e^-) Lab}$

$p_{y(e^-) CM}= p_{y((e^-) Lab}$

$\Longrightarrow\begin{cases} E_{Lab}=\gamma_{Lab} (E_{ CM})+\beta_{Lab} \gamma_{Lab} p_{z CM} \\ p_{z Lab}=\beta_{Lab} \gamma_{Lab}(E_{ CM})+ \gamma_{Lab}p_{z CM} \end{cases}$

$\Longrightarrow\begin{cases} \gamma_{Lab} = \frac{E_{ Lab}}{E_{CM}} \\ \beta_{Lab} =\frac{p_{zLab}}{E_{LAB}} \end{cases}$

Without knowing the values for gamma or beta, we can use the fact that lengths of the two 4-momenta are invariant

$s={\mathbf P}_{CM}^2=(E_{(e^-) CM}+E_{(m) CM})^2-(\vec p_{(e^-) CM}+\vec p_{(m) CM})^2$

$s={\mathbf P}_{Lab}^2=(E_{(e^-) Lab}+E_{(m) Lab})^2-(\vec p_{(e^-) Lab}+\vec p_{(m) Lab})^2$

Setting these equal to each other, we can use this for the collision of two particles of mass m₁ and m₂. Since the total momentum is zero in the Center of Mass frame, we can express total energy in the center of mass frame as

$(E_{1 CM}+E_{2 CM})^2-(\vec p_{1 CM}+\vec p_{2 CM})^2=s=(E_{1 Lab}+E_{2 Lab})^2-(\vec{p_{1 Lab}}+\vec p_{2 Lab})^2$

$(E_{CM})^2-(\vec p_{CM})^2=(E_{1 Lab}+E_{2 Lab})^2-(\vec{p_{Lab}})^2$

$(E_{CM})^2=(E_{Lab})^2-(\vec{p_{Lab}})^2$

$(E_{CM})^2+(\vec{p_{Lab}})^2=(E_{Lab})^2$

$E_{Lab}=\sqrt{(E_{CM})^2+(\vec{p_{Lab}})^2}$

Since momentum is conserved, the initial momentum from the incident electron and stationary electron is still the same in the Lab frame, therefore $p_{Lab}=11000 MeV$

$E_{Lab}=\sqrt{(106.031 MeV)^2+(11000 MeV)^2}\approx 11000.511 MeV$

This is the same as the initial total energy in the Lab frame, which should be expected since scattering is considered to be an elastic collision.

Since,

$E_{Lab}\equiv E_{(e^-)Lab}+E_{(m)Lab}$

$\Longrightarrow E_{(e^-)Lab}=E_{Lab}-E_{(m)Lab}$

Using the relation

$E^2\equiv p^2+m^2$

$\Longrightarrow p_{(e^-)Lab}^2=E_{(e^-)Lab}^2-m_{(e^-)Lab}^2=E_{(e^-)Lab}^2-(.511 MeV)^2$

Using

$p^2 \equiv p_x^2+p_y^2+p_z^2$

$\Longrightarrow p_{(e^-)z Lab}=\sqrt{p_{(e^-)Lab}^2-p_{(e^-)xLab}^2-p_{(e^-)Lab}^2}$

DV_RunGroupC_Moller#Momentum distributions in the Center of Mass Frame

DV_MollerTrackRecon#Calculations_of_4-momentum_components