DV RunGroupC Moller

Simulating the Moller scattering background for EG1

Step 1

Determine the Moller background using an LH2 target to check the physics in GEANT4

Incident electron energy varies from 1-11 GeV.

LH2 target is a cylinder with a 1.5 cm diameter and 1 cm thickness.

  (Following dimensions listed on page 8 of File:PHY02-33.pdf)

Numbers Moller electrons per incident electron.

  While 2nd and 3rd generations are created, only 2 2nd generation daughter particles are created for 1E6 incident particles.  All knock on electrons are not counted.

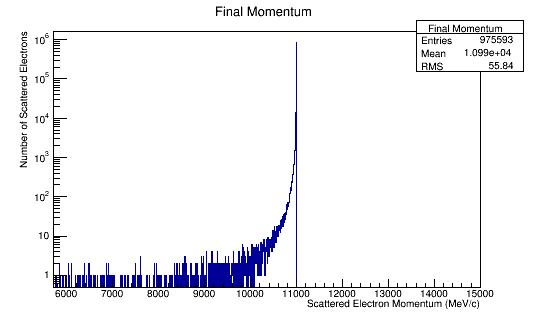
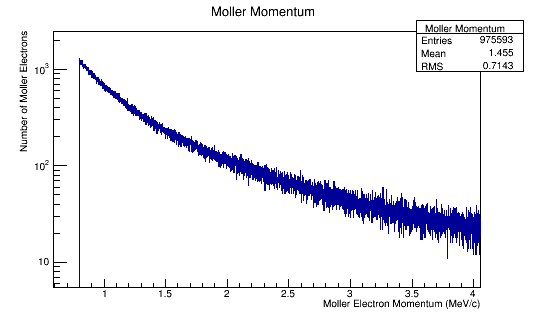
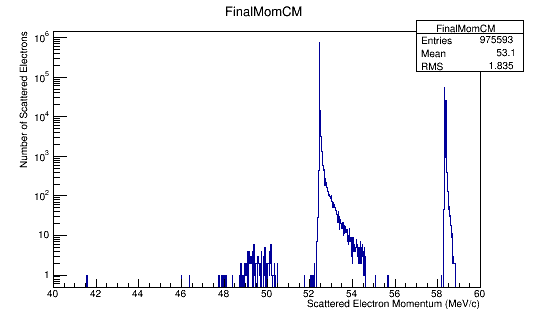
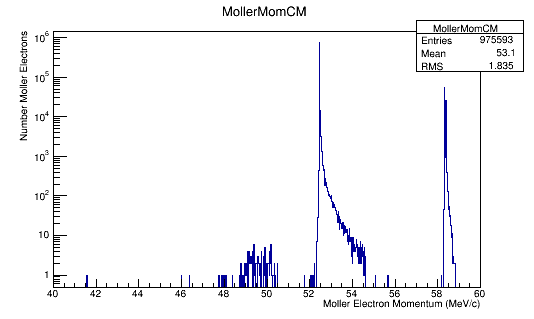
Momentum distributions.

In the collision of two particles of mass m_1 and m_2, the total energy in the center of mass frame can be written

[math]E_{cm}={(E_1+E_2)^2-(p_1+p_2)^2}[/math]

[math]E_{cm}=[m_1^2+m_2^2+2E_1E_2(1-β_1β_2cosθ)]^{1/2}[/math]

where θ is the angle between the particles. In the frame where one particle (m₂) is at rest

E_cm=(m₁²+m₂²+2E_{1 lab}m₂)^1/2

The velocity of the center of mass in the lab frame is

β_cm=p_lab/(E_{1 lab}+m₂),

where p_lab≡p_{1 lab} and

γ_cm(E_{1 lab}+m₂)/E_cm

This gives the momenta of the particles in the center of mass to have equal magnitude, but opposite directions

p_cm=p_labm₂/E_cm

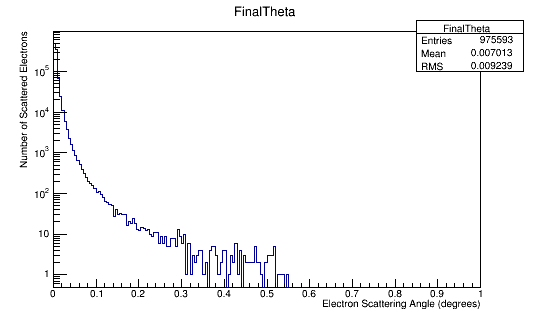
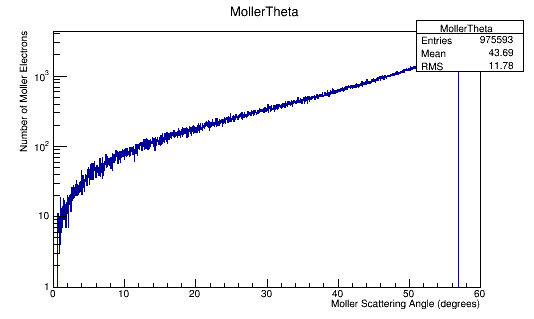
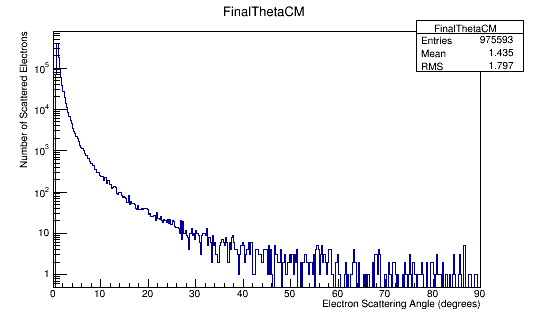
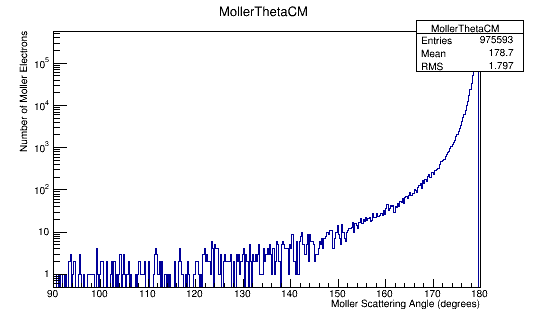
For an incoming electron with momentum of 11GeV, we should find the momentum in the center of mass to be around 53 MeV which is confirmed in the the plots.

Sample output from GEANT4 simulation:

KEi	Pxi	Pyi	Pzi	xi	yi	zi	KEf	Pxf	Pyf	Pzf	xf	yf	zf	KEm	Pxm	Pym	Pzm	xm	ym	zm
11000	0	0	11000.5	0	0	-510	10999.1	0.433025	-0.858867	10999.6	0	0	-509.276	0.905324	-0.433025	0.858867	0.905366	0	0	-509.276

Running a GEANT simulation just to put this set into a .dat file, then using the .dat file through the Moller_OG.C file in ROOT, we find in the Lab Frame:

Fnl4Mom.P 10999.599651
Fnl4Mom.E 10999.610609
Mol4Mom.P 1.320928
Mol4Mom.E 1.416324
Fnl4Mom.Theta(degrees) 0.005013
Fnl4Mom.Theta(radians) 0.000087
Mol4Mom.Theta(degrees) 46.756514
Mol4Mom.Theta(radians) 0.815641

Fnl4Mom.P 52.455386
Fnl4Mom.E 54.704969
Mol4Mom.P 52.455386
Mol4Mom.E 52.457875
Fnl4Mom.Theta(degrees) 1.051202
Fnl4Mom.Theta(radians) 0.018338
Mol4Mom.Theta(degrees) 179.040096
Mol4Mom.Theta(radians) 3.123255

Comparing experimental vs. theoretical for Møller differential cross section 11GeV

Using the equation from Halzen and Martin (p121) to approximate Moller scattering (in the Center of Mass Frame)

[math]\frac{d\sigma}{d\Omega}=\frac{m^2 \alpha^2}{16 p^4}\left(\frac{1}{\sin^4 \frac{\theta}{2}}+\frac{1}{\cos^4 \frac{\theta}{2}}-\frac{1}{\sin^2 \frac{\theta}{2}\cos^2 \frac{\theta}{2}}\right)[/math]

where [math]\alpha = \frac{1}{137}[/math]

Plugging in the values expected for a scattering electron:

[math]m^2 = \frac{(.000511 GeV)^2}{c^4}=2.6\times 10^{-7} GeV^2/c^4[/math]

[math]\alpha^2=\frac{1}{137^2}=7.3\times 10^{-3}[/math]

[math]p^4=\frac{(.053 GeV)^4}{c^4}=7.9\times 10^{-6} GeV^4/c^4[/math]

Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around

[math]\frac{m^2 \alpha^2}{16 p^4}=\frac{1.5\times 10^{-5}}{ GeV^{2}}[/math]

Using the conversion of

[math]\frac{1}{1GeV^{2}}=.3892 mb [/math]

We find that the differential cross section is [math]5.8\times 10^{-6} mb=5.8 nb[/math]

Converting the number of electrons to barns,

[math]L=\frac{i_{scattered}}{\sigma} \approx i_{scattered}\times \rho_{target}\times l_{target}[/math]

where ρ_target is the density of the target material, l_target is the length of the target, and i_scattered is the

[math]L=\frac{70.85 kg}{1 m^3}\times \frac{1 mole}{2.02 g} \times \frac{1000g}{1 kg} \times \frac{6\times10^{23} atoms}{1 mole} \times \frac{1cm}{100 cm} \times \frac{1 m}{ } \times \frac{10^{-23} m^2}{barn} =2.10\times 10^{-2} barns[/math]

[math]\frac{1}{L \times 4\times 10^7}=1.19\times 10^{-6} barns[/math]

Step 2

Replace the LH2 target with an NH3 target and compare with LH2 target.

Step 3

Determine impact of Solenoid magnet on Moller events

Papers used

A polarized target for the CLAS detectorFile:PHY02-33.pdf

An investigation of the spin structure of the proton in deep inelastic scattering of polarized muons on polarized protons File:1819.pdf

EG12