Difference between revisions of "Forest UCM MiNF"
Jump to navigation
Jump to search
| Line 33: | Line 33: | ||
where | where | ||
| − | : <math>\vec {F}_{\mbox {inertial}} = m \vec A \equiv</math> inertial force ( an example is the centrifugal force for rotational acceleration) | + | : <math>\vec {F}_{\mbox {inertial}} = m \vec A \equiv</math> inertial force ( an example is the "fictional" centrifugal force for rotational acceleration) |
[[Forest_Ugrad_ClassicalMechanics]] | [[Forest_Ugrad_ClassicalMechanics]] | ||
Revision as of 13:26, 3 November 2014
Mechanics in Noninertial Reference Frames
Linearly accelerating reference frames
Let represent an inertial reference frame and \mathcal S represent an noninertial reference frame with acceleration relative to .
Ball thrown straight up
Consider the motion of a ball thrown straight up as viewed from .
Using a Galilean transformation (not a relativistic Lorentz transformation)
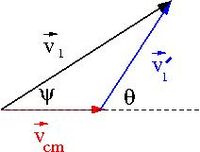
At some instant in time the velocities add like
where
- = velocity of moving frame with respect to at some instant in time
taking derivative with respect to time
where
- inertial force ( an example is the "fictional" centrifugal force for rotational acceleration)