Difference between revisions of "Forest UCM CoV"
| Line 7: | Line 7: | ||
Fermats principle is that light takes a path between two points that requires the least amount of time. | Fermats principle is that light takes a path between two points that requires the least amount of time. | ||
| + | |||
| + | [[File:TF_Fermat_LawSines.png|| 400 px]] | ||
If we let S represent the path of light between two points then | If we let S represent the path of light between two points then | ||
| Line 41: | Line 43: | ||
or | or | ||
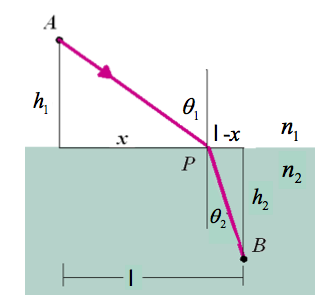
| − | :<math> \Rightarrow n_1\sin(\theta_1) = n_2 \sin(\theta_2) </math> | + | :<math> \Rightarrow n_1\sin(\theta_1) = n_2 \sin(\theta_2) </math> |
==Generalizing Fermat's principle to determining the shorest path== | ==Generalizing Fermat's principle to determining the shorest path== | ||
Revision as of 15:26, 13 October 2014
Calculus of Variations
Fermat's Principle
Fermats principle is that light takes a path between two points that requires the least amount of time.
If we let S represent the path of light between two points then
light takes the time to travel between two points can be expressed as
The index of refraction is denoted as
for light traversing an interface with an nindex of refraction $n_1$ on one side and $n_2$ on the other side we would hav e
take derivative of time with respect to to find a minimum for the time of flight
or
Generalizing Fermat's principle to determining the shorest path
One can apply Fermat's principle to show that the shortest path between two points is a straight line.
In 2-D one can write the differential path length as
using chain rule
the the path length between two points and is
adding up the minimum of the integrand function is one way to minimize the integral ( or path length)
let
a critical point (where a min or max) exists if
if the second derivative is zero there is a min, max, or neither
if the second derivative is negative there is a max
if the second derivative is positive there is a min
http://scipp.ucsc.edu/~haber/ph5B/fermat09.pdf
Euler-Lagrange Equation
https://www.fields.utoronto.ca/programs/scientific/12-13/Marsden/FieldsSS2-FinalSlidesJuly2012.pdf