Difference between revisions of "Forest UCM NLM AtwoodMachine"
Jump to navigation
Jump to search
| Line 30: | Line 30: | ||
== Step 4: Define the Force vectors using the above coordinate system== | == Step 4: Define the Force vectors using the above coordinate system== | ||
| + | ;for mass 1 | ||
| + | :<math>T_1 - m_1 g = m_1 a_1</math> | ||
| + | ;for mass 2 | ||
| + | :<math>T_2 - m_2 g = m_2 a_2</math> | ||
| + | |||
| + | ;for mass 3 | ||
| + | :<math>T_3 - m_3 g = m_3 a_3</math> | ||
==Step 5: Use Newton's second law== | ==Step 5: Use Newton's second law== | ||
Revision as of 11:31, 22 August 2014
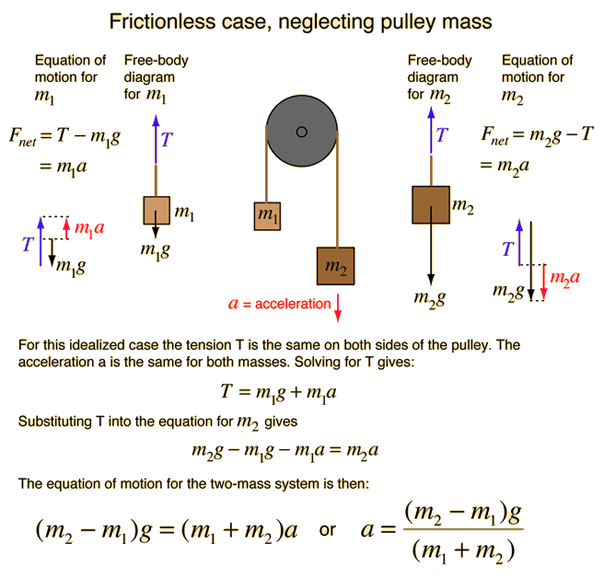
Simple Atwood's machine
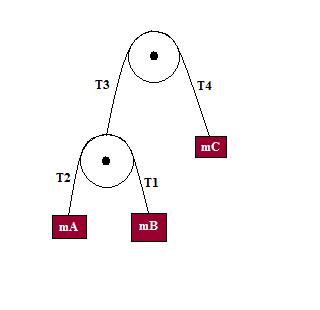
Double Atwood's machine
The problem
Determine the acceleration of each mass in the above picture.
Step 1: Identify the system
- Each block is a separate system with two external forces; a gravitational force and the rope tension.
Step 2: Choose a suitable coordinate system
- A coordinate system with one axis that defines the posive direction as up is one possible orientation.
Step 3: Draw the Free Body Diagram
Step 4: Define the Force vectors using the above coordinate system
- for mass 1
- for mass 2
- for mass 3