Difference between revisions of "Forest UCM NLM"
| Line 107: | Line 107: | ||
:<math>\vec{a} = \frac{d \vec{v}}{dt} =\vec{\ddot{r}} </math> | :<math>\vec{a} = \frac{d \vec{v}}{dt} =\vec{\ddot{r}} </math> | ||
::<math>= \frac{ d \left (\dot{r} \hat{r} + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}\right)}{dt}</math> | ::<math>= \frac{ d \left (\dot{r} \hat{r} + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}\right)}{dt}</math> | ||
| − | ::<math>= \frac{ d \dot{r}}{dt} \hat{r} + \dot{r} \frac{ d\hat{r}}{dt} + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}\right)}{dt}</math> | + | ::<math>= \left ( \frac{ d \dot{r}}{dt} \hat{r} + \dot{r} \frac{ d\hat{r}}{dt} \right) + r \dot{\phi} \hat{\phi}= v_r \hat{r} + v_{\phi} \hat{\phi}\right)}{dt}</math> |
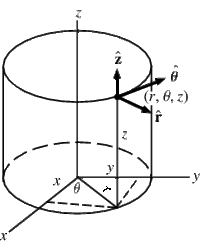
===Cylindrical=== | ===Cylindrical=== | ||
Revision as of 21:13, 18 June 2014
Newton's Laws of Motion
Limits of Classical Mechanic
Classical Mechanics is the formulations of physics developed by Newton (1642-1727), Lagrange(1736-1813), and Hamilton(1805-1865).
It may be used to describe the motion of objects which are not moving at high speeds (0.1) nor are microscopically small ( ).
The laws are formulated in terms of space, time, mass, and force:
Space and Time
Space
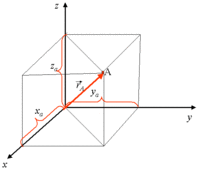
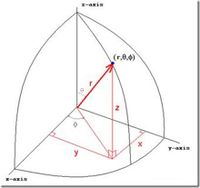
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.
Cartesian
Vector Notation convention:
Position:
Velocity:
- = =
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- = =
Similarly Acceleration is given by
- = =
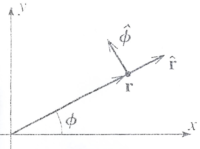
Polar
Position:
Because points in a unique direction given by we can write the position vector as
- : does not have the units of length
The unit vectors ( and ) are changing in time. You could express the position vector in terms of the cartesian unit vectors in order to avoid this
The dependence of position with can be seen if you look at how the position changes with time.
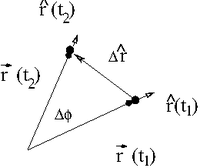
Velocity in Polar Coordinates
Consider the motion of a particle in a circle. At time the particle is at and at time the particle is at
If we take the limit ( or ) then we can write the velocity of this particle traveling in a circle as
- or
Thus for circular motion at a constraint radius we get the familiar expression
If the particle is not constrained to circular motion ( i.e.: can change with time) then the velocity vector in polar coordinates is
- =
- or in more compact form
Acceleration in Polar Coordinates
Taking the derivative of velocity with time gives the acceleration
Cylindrical
Spherical