Difference between revisions of "Forest UCM NLM"
(→Polar) |
|||
| Line 41: | Line 41: | ||
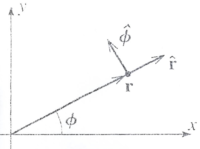
===Polar=== | ===Polar=== | ||
[[File:TF_UCM_PolarCoordSys.png| 200 px]] | [[File:TF_UCM_PolarCoordSys.png| 200 px]] | ||
| + | Vector Notation convention: | ||
| + | Position: | ||
| + | :<math>\vec{r} = r \hat{r}</math> | ||
| + | |||
| + | |||
| + | |||
| + | Velocity: | ||
| + | |||
| + | :<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + x\frac{d \hat{i}}{dt} + cdots</math> | ||
| + | |||
| + | |||
| + | cartesian unit vectors do not change with time (unit vectors for other coordinate system types do) | ||
| + | |||
| + | |||
| + | :<math>\frac{d \hat{i}}{dt} =0 =\frac{d \hat{j}}{dt} =\frac{d \hat{k}}{dt}</math> | ||
| + | |||
| + | :<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{i} + \frac{d z}{dt}\hat{i} </math> | ||
| + | |||
| + | |||
| + | The unit vectors are changing in time. You could express the position vector in terms of cartesian unit vector in order to avoid this | ||
| + | |||
| + | :<math>\vec{r} = r \cos(\phi) \hat{i} + r \sin(\phi)\hat{j}</math> | ||
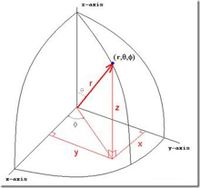
===Spherical=== | ===Spherical=== | ||
Revision as of 21:10, 17 June 2014
Newton's Laws of Motion
Limits of Classical Mechanic
Classical Mechanics is the formulations of physics developed by Newton (1642-1727), Lagrange(1736-1813), and Hamilton(1805-1865).
It may be used to describe the motion of objects which are not moving at high speeds (0.1) nor are microscopically small ( ).
The laws are formulated in terms of space, time, mass, and force:
Space and Time
Space
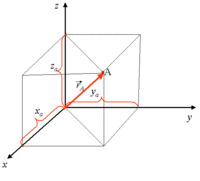
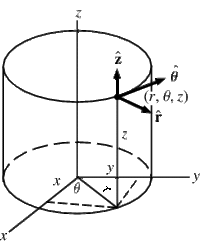
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.
Cartesian
Vector Notation convention:
Position:
Velocity:
- = =
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- = =
Polar
Position:
Velocity:
- = =
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- = =
The unit vectors are changing in time. You could express the position vector in terms of cartesian unit vector in order to avoid this