Difference between revisions of "Forest UCM NLM"
Jump to navigation
Jump to search
| Line 23: | Line 23: | ||
Vector Notation convention: | Vector Notation convention: | ||
| − | Position:<math>\vec{r} = x \hat{i} + y \hat{j} + z \hat{k} = (x,y,z) = \sum_1^3 r_i \hat{e}_i</math> | + | Position: |
| + | |||
| + | ;<math>\vec{r} = x \hat{i} + y \hat{j} + z \hat{k} = (x,y,z) = \sum_1^3 r_i \hat{e}_i</math> | ||
Velocity: | Velocity: | ||
| − | <math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + x\frac{d \hat{i}}{dt} + …</math> = | + | |
| + | :<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + x\frac{d \hat{i}}{dt} + …</math> = | ||
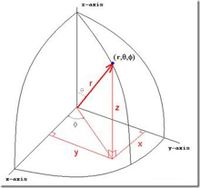
===Spherical=== | ===Spherical=== | ||
Revision as of 18:27, 12 June 2014
Newton's Laws of Motion
Limits of Classical Mechanic
Classical Mechanics is the formulations of physics developed by Newton (1642-1727), Lagrange(1736-1813), and Hamilton(1805-1865).
It may be used to describe the motion of objects which are not moving at high speeds (0.1) nor are microscopically small ( ).
The laws are formulated in terms of space, time, mass, and force:
Space and Time
Space
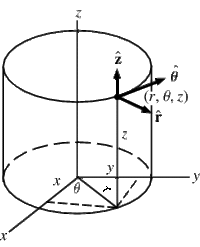
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.
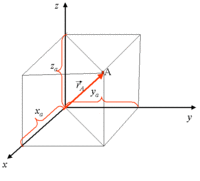
Cartesian
Vector Notation convention:
Position:
Velocity:
- = = =
Spherical
Cylindrical
