Difference between revisions of "SIDIS CLASNOTE 2013"
| Line 92: | Line 92: | ||
The CLAS electromagnetic calorimeter was used to reduce the misidentification of negatively charged pions as electron candidates. The electromagnetic calorimeter contains thirteen layers of lead-scintillator sandwiches composed of 2 mm thick lead and 10 mm thick scintillator sections. Each set of thirteen layers is subdivided into five inner and eight outer layers that are named the inner and outer calorimeter respectively. | The CLAS electromagnetic calorimeter was used to reduce the misidentification of negatively charged pions as electron candidates. The electromagnetic calorimeter contains thirteen layers of lead-scintillator sandwiches composed of 2 mm thick lead and 10 mm thick scintillator sections. Each set of thirteen layers is subdivided into five inner and eight outer layers that are named the inner and outer calorimeter respectively. | ||
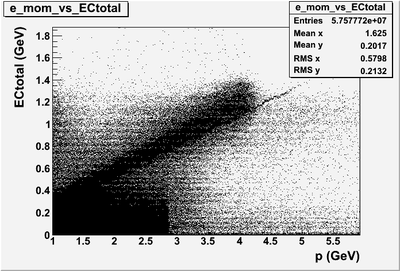
Electrons interacting with the calorimeter produce electromagnetic showers that release energy into the calorimeter. The deposited energy is proportional to the momentum of the electrons. Figure 1.3 shows the correlation of | Electrons interacting with the calorimeter produce electromagnetic showers that release energy into the calorimeter. The deposited energy is proportional to the momentum of the electrons. Figure 1.3 shows the correlation of | ||
| − | the inner and outer calorimeter electron candidate’s energy measured by the calorimeter and divided by the particles momentum reconstructed by the drift chamber. As shown in | + | the inner and outer calorimeter electron candidate’s energy measured by the calorimeter and divided by the particles momentum reconstructed by the drift chamber. As shown in Figure 1.3, there is an island near E/p = 0.2, which contains most of the electron candidates as well as some regions below 0.2 which will be argued to be negative pions misidentified as electrons. |
| − | Pions entering the calorimeter are typically minimum ionizing particles, loosing little of their incident energy in the calorimeter at a rate of 2 <math>MeV cm^2/g</math>. Electrons, on the other hand, deposit a larger fraction of their momentum into the calorimeter. As a result, the energy deposited into the electromagnetic calorimeter is different for electrons and pions. Pions loose about 0.08 GeV of energy traversing the calorimeter independent their momentum thereby producing | + | |
| + | Pions entering the calorimeter are typically minimum ionizing particles, loosing little of their incident energy in the calorimeter at a rate of 2 <math>MeV cm^2/g</math>. Electrons, on the other hand, deposit a larger fraction of their momentum into the calorimeter. As a result, the energy deposited into the electromagnetic calorimeter is different for electrons and pions. Pions loose about 0.08 GeV of energy traversing the calorimeter independent their momentum thereby producing a constant signal in the calorimeter around 0.08 GeV. In order to reduce misidentified pions from the electron sample, the following cut | ||
{| border="0" style="background:transparent;" align="center" | {| border="0" style="background:transparent;" align="center" | ||
| Line 107: | Line 108: | ||
and results in the following cut for the energy deposition into the outer layer of the calorimeter: | and results in the following cut for the energy deposition into the outer layer of the calorimeter: | ||
ECtot > 0.2 × p. (1.3) | ECtot > 0.2 × p. (1.3) | ||
| + | |||
Cherenkov Counter Cut | Cherenkov Counter Cut | ||
| − | The Cherenkov counter has been used to further reduce the negatively charged pion background in the reconstructed electron sample. When the | + | |
| + | The Cherenkov counter has been used to further reduce the negatively charged pion background in the reconstructed electron sample. When the velocity of a charged particle is greater than the local phase velocity of light or when it enters a medium with different optical properties, the charged particle can emit photons. Cherenkov light is emitted at the critical angle<math> \theta_c</math> representing the angle of Cherenkov radiation relative to the particle’s direction. It can be | ||
has been applied: | has been applied: | ||
| Line 161: | Line 164: | ||
(1.8) | (1.8) | ||
| − | The gas used in the CLAS Cerenkov counter is perfluorobutane C4F10 with index of refraction equal to 1.00153. Approximately thirteen photoelec- trons are produced by electrons traversing the Cherenkov detector. On the | + | The gas used in the CLAS Cerenkov counter is perfluorobutane C4F10 with an index of refraction equal to 1.00153. Approximately thirteen photoelec- trons are produced by electrons traversing the Cherenkov detector. On the |
| − | |||
other hand, calculations show that the number of photons produced by the negatively charged pions in the Cherenkov detector is approximately two. The theoretical results of the number of photons produced by the electrons and pions when passing through the Cherenkov counter are shown on Figure 1.4. | other hand, calculations show that the number of photons produced by the negatively charged pions in the Cherenkov detector is approximately two. The theoretical results of the number of photons produced by the electrons and pions when passing through the Cherenkov counter are shown on Figure 1.4. | ||
(a) For electrons. | (a) For electrons. | ||
| Line 179: | Line 181: | ||
|<math>|\theta_{p} - {\theta_{p}}^{\mbox {\rm center}} - {\theta_{p}}^{\mbox{\rm offset}}| < 3 \sigma_{p}</math>|}, (1.9) | |<math>|\theta_{p} - {\theta_{p}}^{\mbox {\rm center}} - {\theta_{p}}^{\mbox{\rm offset}}| < 3 \sigma_{p}</math>|}, (1.9) | ||
| − | where θp represents the measured polar angle with respect to a projectile plane for each electron event and σp the width of the polar angle θp. The Cherenkov counter’s projective plane is an imaginary plane behind the Cherenkov detector where Cherenkov radiation would have arrived if it had moved the same distance from emission point to the PMT, without reflections in the mirror system. θpcenter is the polar angle from the CLAS detector center to the image of Cherenkov counter segment center and θpoffset is the shift in the segment center position. In addition to geometrical cuts, timing cuts have been applied to match the time between a Cherenkov counter hit and the time of flight system. | + | where θp represents the measured polar angle with respect to a projectile plane for each electron event and σp the width of the polar angle θp. The Cherenkov counter’s projective plane is an imaginary plane behind the Cherenkov detector where Cherenkov radiation would have arrived if it had moved the same distance from the emission point to the PMT, without reflections in the mirror system. θpcenter is the polar angle from the CLAS detector center to the image of Cherenkov counter segment center and θpoffset is the shift in the segment center position. In addition to geometrical cuts, timing cuts have been applied to match the time between a Cherenkov counter hit and the time of flight system. |
The pion contamination in an electron sample was estimated by fitting the photoelectron distribution using two Gaussian distributions convoluted with a Landau distribution [4]: | The pion contamination in an electron sample was estimated by fitting the photoelectron distribution using two Gaussian distributions convoluted with a Landau distribution [4]: | ||
−0.5“ x−p1 ”2 1 −0.5“ x−p7 ”2 | −0.5“ x−p1 ”2 1 −0.5“ x−p7 ”2 | ||
Revision as of 20:55, 14 June 2013
sample TeX file for CLAS note
Abstract
Semi-inclusive deep inelastic scattering (SIDIS) experiments may be used to identify the flavor of the quark that participates in the scattering process. Semi-inclusive scattering is defined as an electron scattering experiment in which the scattered electron and one hadron are detected in the final state. Experiments at Jefferson Lab have used longitudinally polarized electrons to probe longitudinally polarized hydrogen and deuterium targets and investigate the quark’s contribution to nucleon properties. This work reports on a measurement of SIDIS pion asymmetries using the CEBAF Large Acceptance Spectrometer (CLAS) at Thomas Jefferson National Accelerator Facility. The incident electron’s energy was 4.2 GeV and covered a kinematic region where the struck quark carries at least 30% of the nucleons total momentum (). The electrons scatter mostly from valence quarks in this kinematic region allowing measurements which are less sensitive to the ocean of quark-antiquark pairs that are also inside a nucleon.
Data Analysis
Semi-inclusive deep inelastic scattering (SIDIS) experiments using longitudinally polarized hydrogen and deuterium targets and a longitudinally polarized electron beam can be used to measure the fractional polarization of down quarks in the nucleon . Semi-inclusive scattering identifies an electron scattering experiment in which the scattered electron and one hadron are detected in the final state. This chapter describes the techniques used to analyze the data collected during the EG1b experiment and calculate semi-inclusive cross sections for the following reactions:
and
using NH3 and ND3 polarized targets respectively. The goal of this work is to measure charged pion asymmetries defined according to the incident electron helicity and the target polarization. This work focuses on a kinematic region where the struck quark carries at least 30% of the nucleons total momentum . The leptons scatter mostly from valence quarks in this kinematic region allowing contributions from sea quarks to be neglected. The above measurements are able to distinguish between the predictions made by the hyperfine perturbed quark constituent model (pQCM) and perturbative Quantum Chromodynamics (pQCD). As a result, the following study can be used to test the validity of the above models describing the structure of the nucleon.
The CLAS Data Selection
The data files from the EG1b experiment chosen for this analysis are listed in Table 1.1. The experiment probed polarized NH3 and ND3 targets using longitudinally polarized electrons accelerated to three difference energies; 2.2 GeV, 4.2 GeV and 5.7 GeV. This work analyzed the data collected using a 4.2 GeV electron as this energy provided the most statistics. The restrictions applied to the reconstructed events are described in the sections below.
| Run Set | Target Type | Torus Current(A) | Target Polarization | HWP |
| 28100 - 28102 | ND3 | +2250 | -0.18 | +1 |
| 28106 - 28115 | ND3 | +2250 | -0.18 | -1 |
| 28145 - 28158 | ND3 | +2250 | -0.20 | +1 |
| 28166 - 28190 | ND3 | +2250 | +0.30 | +1 |
| 28205 - 28217 | NH3 | +2250 | +0.75 | +1 |
| 28222 - 28236 | NH3 | +2250 | -0.68 | +1 |
| 28242 - 28256 | NH3 | +2250 | -0.70 | -1 |
| 28260 - 28275 | NH3 | +2250 | +0.69 | -1 |
| 28287 - 28302 | ND3 | -2250 | +0.28 | +1 |
| 28306 - 28322 | ND3 | -2250 | -0.12 | +1 |
| 28375 - 28399 | ND3 | -2250 | +0.25 | -1 |
| 28407 - 28417 | NH3 | -2250 | +0.73 | -1 |
| 28456 - 28479 | NH3 | -2250 | -0.69 | +1 |
| Table 1.1. EG1b Runs analyzed for this work. |
Particle Identification
Additional tests were performed on the electron and a pion candidates reconstructed by the standard CLAS software package RECSIS. Electrons are identified by matching the charged particle hits in the Cherenkov counter (CC), electromagnetic calorimeter (EC), and the time of flight system (ToF). The geometrical and timing constraints described in reference [3] were applied to improve electron identification. Additional constraints are applied on the energy deposited by the particle into the calorimeter and the number of photoelectrons produced in the Cherenkov counter. Charged pions are identified by matching the hits in the drift chamber (DC) and ToF counter along with a requirement that the number of photons observed in the CC be less than two for the pions.
Electron Identification
Taylor expanding Eq. 3.6 and keeping only the first two terms we get following
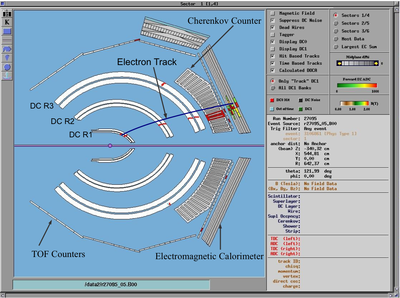
The CLAS trigger system required a particle to deposit energy in the electromagnetic calorimeter and illuminate the Cherenkov counter within a 150 ns time window (Figure 1.1). Unfortunately, this trigger suffers from a back- ground of high energy negative pions that may be misidentified as electrons. The pion contamination of the electron sample is reduced using cuts on the energy deposited in the electromagnetic calorimeter and the momentum measured by reconstructing the particles track in the known magnetic field. The total energy deposited by electron in the EC is proportional to their kinetic energy, whereas the energy deposited by pions is relatively independent of their momentum since the pions entering the EC are minimum ionizing particles(Figure 1.2). Geometrical and time matching cuts between the Cherenkov counter hit and the measured track in the drift chamber were developed to suppress the pion background further.
EC CUTS
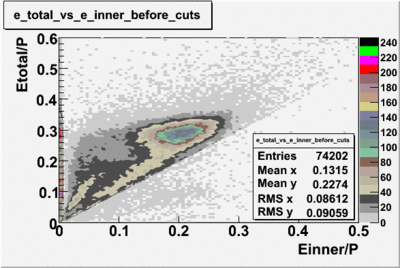
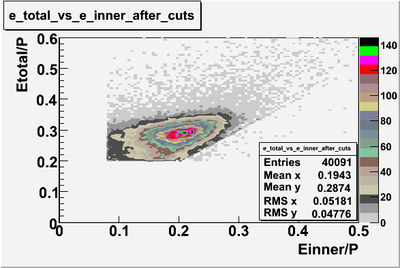
The CLAS electromagnetic calorimeter was used to reduce the misidentification of negatively charged pions as electron candidates. The electromagnetic calorimeter contains thirteen layers of lead-scintillator sandwiches composed of 2 mm thick lead and 10 mm thick scintillator sections. Each set of thirteen layers is subdivided into five inner and eight outer layers that are named the inner and outer calorimeter respectively. Electrons interacting with the calorimeter produce electromagnetic showers that release energy into the calorimeter. The deposited energy is proportional to the momentum of the electrons. Figure 1.3 shows the correlation of the inner and outer calorimeter electron candidate’s energy measured by the calorimeter and divided by the particles momentum reconstructed by the drift chamber. As shown in Figure 1.3, there is an island near E/p = 0.2, which contains most of the electron candidates as well as some regions below 0.2 which will be argued to be negative pions misidentified as electrons.
Pions entering the calorimeter are typically minimum ionizing particles, loosing little of their incident energy in the calorimeter at a rate of 2 . Electrons, on the other hand, deposit a larger fraction of their momentum into the calorimeter. As a result, the energy deposited into the electromagnetic calorimeter is different for electrons and pions. Pions loose about 0.08 GeV of energy traversing the calorimeter independent their momentum thereby producing a constant signal in the calorimeter around 0.08 GeV. In order to reduce misidentified pions from the electron sample, the following cut
ECinner > 0.08 × p, (1.1) where p represents a particle’s momentum and ECinner the energy deposited into the inner part of the calorimeter. Since the energy loss of pions is related to the calorimeter thickness, a correlation can be established between the energy deposited into the inner and outer layers of the calorimeter: ECtot = 13, (1.2) ECinner 5 and results in the following cut for the energy deposition into the outer layer of the calorimeter: ECtot > 0.2 × p. (1.3)
Cherenkov Counter Cut
The Cherenkov counter has been used to further reduce the negatively charged pion background in the reconstructed electron sample. When the velocity of a charged particle is greater than the local phase velocity of light or when it enters a medium with different optical properties, the charged particle can emit photons. Cherenkov light is emitted at the critical angle representing the angle of Cherenkov radiation relative to the particle’s direction. It can be
has been applied: 
Fig. 1.3: ECinner/p versus ECtot/p before and after EC cuts (ECtot > 0.2p and ECinner > 0.08p). After applying EC cuts about 46% of the events have been removed from the electron sample. shown that the cosine of the Cherenkov radiation angle is inversely proportional to the velocity of the charged particle cosθc = 1 , (1.4) nβ
where βc is the particle’s velocity and n the index of refraction of the medium. The charged particle in time t travels a distance βct, while the electromagnetic waves travel c t. For a medium with given index of refraction n, there is a n threshold velocity βthr = 1 , below which no radiation is emitted. This process n may be used to distinguish between the highly relativistic electrons and the less relativistic pions based on the number of photons produced in the Cherenkov detector. The number of photons produced per unit path length of a particle with charge Ze and per unit energy interval of the photons is proportional to the sine of the Cherenkov angle [2]