Difference between revisions of "Runs 4111(D2O)/4112(H2O)"
| Line 33: | Line 33: | ||
The above plot may look better if you plot <math>Energy</math> -vs- (<math>Energy \pm Energy</math>) | The above plot may look better if you plot <math>Energy</math> -vs- (<math>Energy \pm Energy</math>) | ||
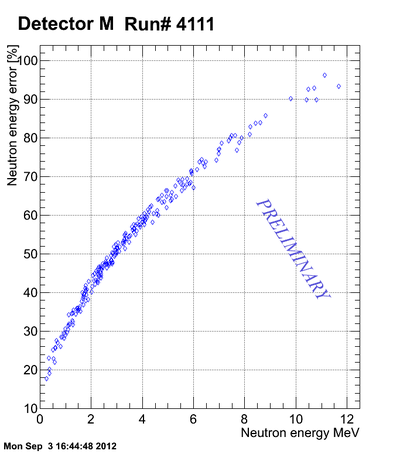
As the energy increased the uncertainty increases to the point the the error bar is as big as the magnitude of the energy. | As the energy increased the uncertainty increases to the point the the error bar is as big as the magnitude of the energy. | ||
| + | |||
| + | Simulation of the flight pass length uncertainty <math>U(l_n)</math>: | ||
Revision as of 21:11, 10 September 2012
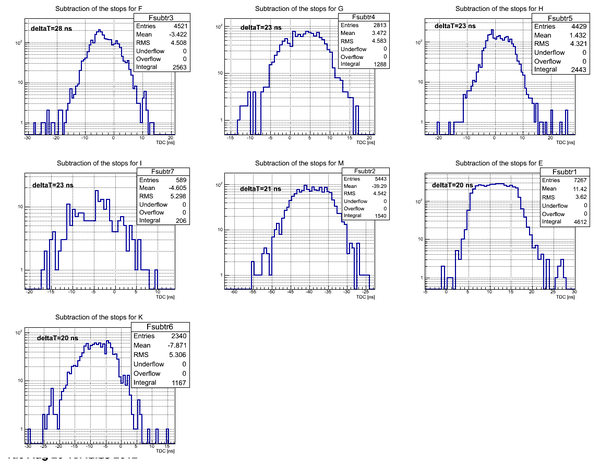
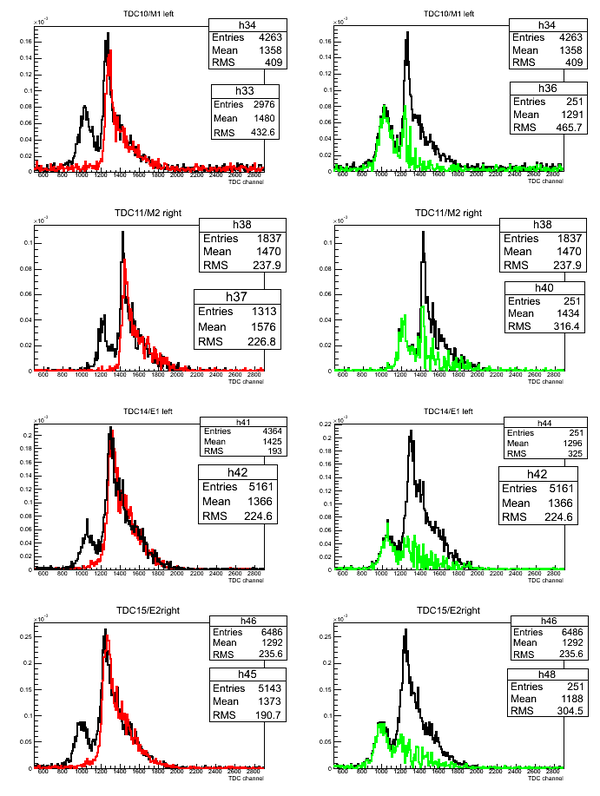
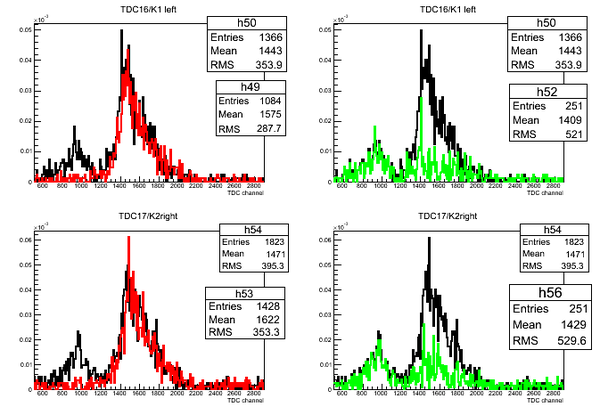
Subtraction of the stops for each detector in the case of D2O target. The length of the active area (scintillator) of the detector is 75.3 cm.
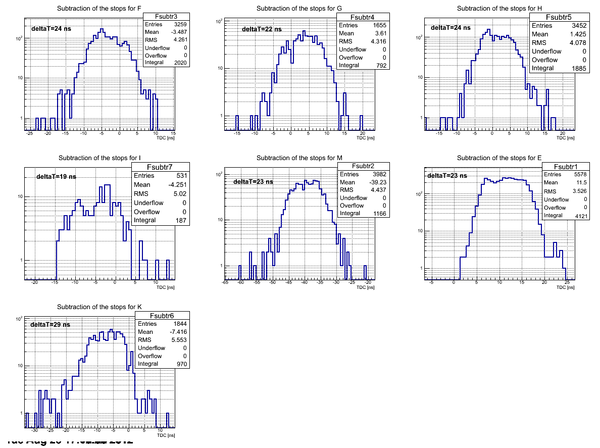
Subtraction of the stops for each detector in the case of H2O target:
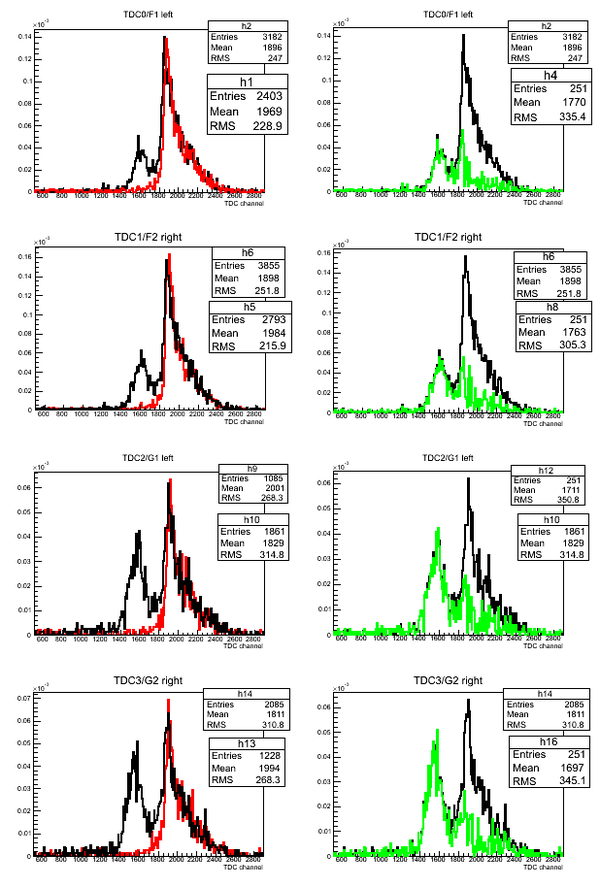
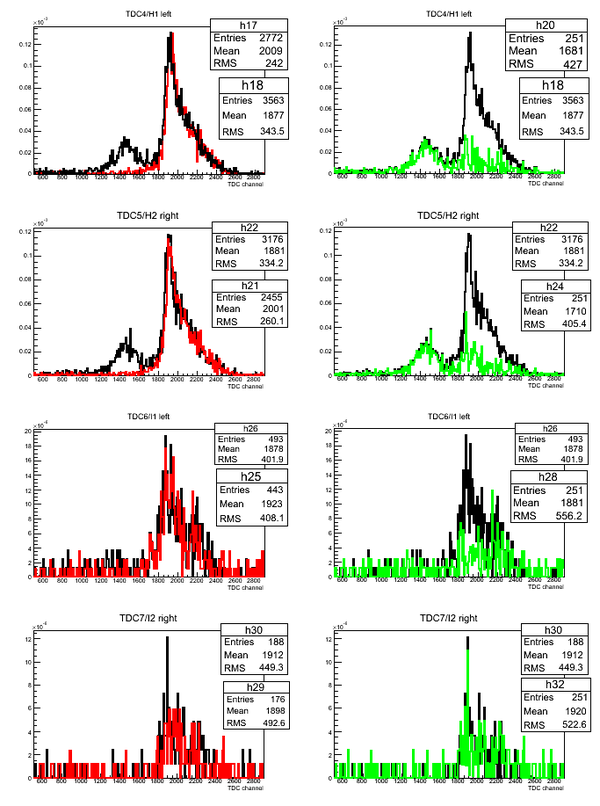
Normalized superimposed timing spectra from D2O(black line)/H2O(red line) targets and bin-by-bin subtraction (green line) of D2O-H2O data:
Neutron energy distribution data analysis for run 4111:
Errors on the neutron energy for the case of Det M:
Where uncertainty in the neutron flight pass due to the finite width of the detector (14.8 cm) and uncertainty in zero time definition in neutron TOF spectrum
Correlation between the neutron energy and neutron energy uncertainty is plotted below:
The above plot may look better if you plot -vs- () As the energy increased the uncertainty increases to the point the the error bar is as big as the magnitude of the energy.
Simulation of the flight pass length uncertainty :