Difference between revisions of "HRRL 03-17-2011"
| Line 223: | Line 223: | ||
y = (3.67838 +-0.02232) + (-4.17265+-0.22057)*x + (5.55113+-0.42056)*x.*x | y = (3.67838 +-0.02232) + (-4.17265+-0.22057)*x + (5.55113+-0.42056)*x.*x | ||
| + | |||
| + | |||
| + | |||
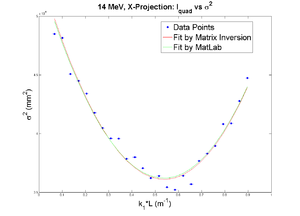
| + | <math> \sigma_x^2= (3.678 \pm 0.022) + (-4.17 \pm 0.22)k_1L + (5.55 \pm 0.42)(k_1L)^2 </math> | ||
| + | |||
| + | <math> \epsilon_x = 0.417 \pm 0.023~mm*mrad ~\Rightarrow~ \epsilon_{n,x} = 11.43 \pm 0.64~mm*mrad</math> | ||
| + | |||
| + | <math> \beta_x=1.385 \pm 0.065, \alpha_x=0.97 \pm 0.07 </math> | ||
=== Y === | === Y === | ||
| Line 237: | Line 245: | ||
y = (2.84273 +-0.04370) + (1.02450+-0.51931)*x + (3.79913+-1.23728)*x.*x | y = (2.84273 +-0.04370) + (1.02450+-0.51931)*x + (3.79913+-1.23728)*x.*x | ||
| + | |||
| + | |||
| + | |||
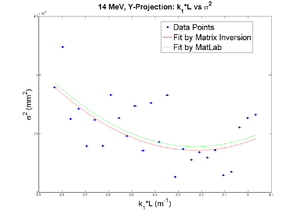
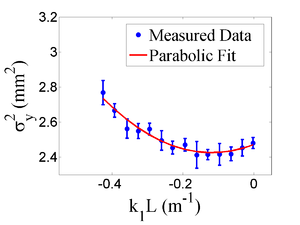
| + | <math>\sigma_y^2 = (2.843 \pm 0.044) + (1.02 \pm 0.52)k_1L + (3.8 \pm 1.2)(k_1L)^2 </math> | ||
| + | |||
| + | <math> \epsilon_y = 0.338 \pm 0.065~mm*mrad ~\Rightarrow~ \epsilon_{n,y} = 9.3 \pm 1.8~mm*mrad</math> | ||
| + | |||
| + | <math> \beta_y=1.17 \pm 0.19, \alpha_y=0.22 \pm 0.10 </math> | ||
=== Without thin lens approximation method === | === Without thin lens approximation method === | ||
| Line 243: | Line 259: | ||
In our case <math> \sqrt{k_{1}} \times L_{QM} = \sqrt{0.5} \times 0.1 = 0.07 < 1 </math> | In our case <math> \sqrt{k_{1}} \times L_{QM} = \sqrt{0.5} \times 0.1 = 0.07 < 1 </math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Revision as of 23:36, 27 November 2011
Accelerator Tuning
Good Tune Used for good Scan
By Dr. Kim
Calibration
| image | OTR image | cal_h (mm/px) | cal_v (mm/px) |
 |
 |
0.04308 | 0.04204 |
 |
 |
0.04320 | 0.04228 |
 |
 |
0.04349 | 0.04181 |
 |
 |
0.04323 | 0.04196 |
 |
 |
0.04337 | 0.04212 |
| mean (mm/px) | mean (mm/px) | ||
Results
Q1
At lower current background subtraction gets worse, because singal/noise drops.
42 mA, Positive Current, X projection
emit=0.388 +- 0.008 mm*mrad, emit_norm=10.64 +- 0.22 mm*mrad
beta=1.285 +- 0.024, alpha=0.94 +-0.03
//K1*L(1/m) er K1*L sgima^2(mm) er sigma^2
Media:2011_Mar_Emit_fit_data_x.txt
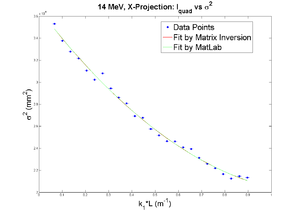
parabola fit for x-projection:
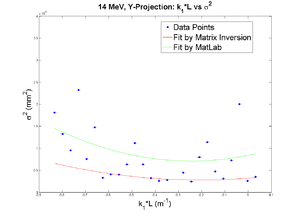
parabola fit for y-projection (y in mm unit):
y = (3.69167 +-0.02346) + (-3.89000+-0.12250)*x + (4.79738+-0.13309)*x.*x
Data created from parabola fit
Media:2011_Mar_Emit_data_from_fit_x.txt
42 mA, Negative Current, Y projection
emit=0.266 +- 0.018 mm*mrad, emit_norm=7.30 +- 0.50 mm*mrad
beta=0.918 +- 0.068, alpha=0.19 +-0.06
//K1*L(1/m) er K1*L sgima^2(mm) er sigma^2
Media:2011_Mar_Emit_fit_data_y.txt
parabola fit for y-projection (y in mm unit):
y = (2.81806 +-0.03890) + (0.52202+-0.26284)*x + (2.35025+-0.34553)*x.*x
Data created from parabola fit
Media:2011_Mar_Emit_data_from_fit_y.txt
X and Y emittances are different. The parabola in X reaches min around 0.4, while in Y reaches around 0.15. Which suggests quadrupole strengths of X and Y are way different for same coil current. Which might suggest beam is not centered, because when beam is off-centered we have this can occur.
20 mA, Positive Current, X projection
10 mA, Positive Current, X projection
5 mA, Positive Current, X projection
Q4
42 mA All Other Quads off
Haven't reach minimum.
42 mA Q1_at_-2A, Q2_at_+8A, Q3_at_-6A
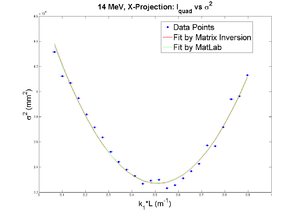
x-projection:
y-projection:
Fits After the Second Mapping of the Quad
MATLAB Scripts
Media:hrrl_2011_marc_emit_test_marc17_SuperGaussian_Fit.txt
Media:hrrl_2011_marc_emit_test_marc17_SupGau_devsum.txt
Media:hrrl_2011_marc_emit_test_marc17_Emit_Parabola_Fit_kl_XProjection.txt
Media:hrrl_2011_marc_emit_test_marc17_Emit_Parabola_Fit_kl_YProjection.txt
Media:hrrl_2011_marc_emit_test_marc17_Trial_my_superGaussian_Fit.txt
Media:hrrl_2011_marc_emit_test_marc17_Plot_Beam_Spot.txt
Media:hrrl_2011_marc_emit_test_marc17_Three_d_surface_plotter.txt
Media:hrrl_2011_marc_emit_test_marc17_my_superGaussian_Fit.txt
Media:hrrl_2011_marc_emit_test_marc17_devsum.txt
Media:hrrl_2011_marc_emit_test_marc17_countor_plotter.txt
With thin lens approximation method
Why y projection has bigger error?
Quad was mapping for the second time to find effective length for the different currents. Link is at [[1]].
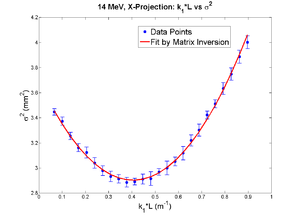
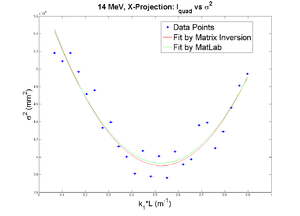
X
x-projection:
emit=0.417 +- 0.023 mm*mrad, emit_norm=11.43 +- 0.64 mm*mrad
beta=1.385 +- 0.065, alpha=0.97 +-0.07
parabola fit for x-projection (y in mm unit):
y = (3.67838 +-0.02232) + (-4.17265+-0.22057)*x + (5.55113+-0.42056)*x.*x
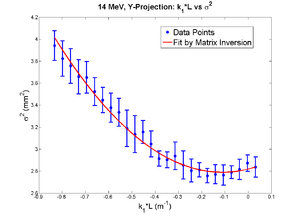
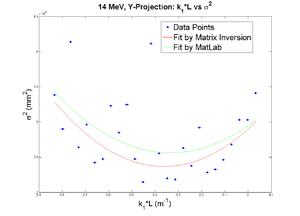
Y
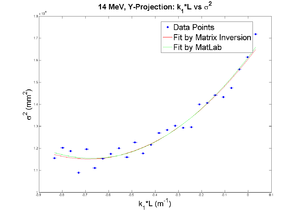
y-projection:
emit=0.338 +- 0.065 mm*mrad, emit_norm=9.25 +- 1.77 mm*mrad
beta=1.170 +- 0.192, alpha=0.22 +-0.10
parabola fit for y-projection (y in mm unit):
y = (2.84273 +-0.04370) + (1.02450+-0.51931)*x + (3.79913+-1.23728)*x.*x
Without thin lens approximation method
Thin lens approximation holds when is true.
In our case