Performance of THGEM as a Neutron Detector

Title

The Performance of Thick Gaseous Electron Multiplier (THGEM) Preamplifiers as a Neutron Sensitive Detector.

Introduction

I propose to construct and measure the performance of a fission chamber instrumented with preamplifiers known as a Thick Gas Electron Multiplier (THGEM). This fission chamber is a chamber filled with a 90/10 Ar/[math]CO_2[/math] gas mixture enclosing a fissionable target material, like Uranium or Thorium. A neutron of sufficient energy has the potential to interact with fissionable material producing heavy ions known as fission fragments. The fission fragments within 5 micron of the target's surface may escape the target as ions and ionize the gas in the chamber. Electrons freed from the ionization gas can enter the THGEM preamplifier producing secondary electrons which are directed to collectors using strong electric fields.

A THGEM preamplifier is a perforated fiberglass board (PC board) clad with a conducting material. The design is based upon the Gas Electron Multiplier (GEM) invented by Fabio Sauli in 1997<ref name="Sauli1997">F. Sauli, et al, NIM A386, (1997) 531-534 </ref >. The GEM preamplifier is a 50 micron sheet of kapton that is coated on each side with 5 micron of copper. The copper clad kapton is perforated with 50-100 micron diameter holes separated by 100-200 micron in a staggered array . The THGEM preamplifier is a more macroscopic version of GEM that uses a 2 mm thick fiberglass sheet perforated with holes that are 2 mm in diameter.

Strong electric fields are established by supplying a potential difference between the two sides of the kapton, or the fiberglass for the case of the THGEM. The electric field lines transport liberated electrons through the preamplifier holes. For the GEM foils, the smaller diameter of the hole can provide sufficient amplification using a potential difference of 350 V between the two sides. On the other hand, the THGEM with the larger hole diameter requires a higher potential difference of about 2000 Volts to achieve similar amplifications.

The objective of this work will be to construct a THGEM based ionization chamber. The THGEM will follow a proven design <ref name="Agocs">G. Agocs, B. Clark, P. Martinego, R. Oliveira, V. Peskov,gand P. Picchi,JINST, 3, P020112, 2008 </ref > and use a resistive paste to reduce discharge events. The detector may be made sensitive to neutrons by doping the resistive paste with a fissionable material. The doping step will take place once a working THGEM equipped detector has been demonstrated. This fission chamber-like device will have the advantage of measuring the location of the incident neutrons that induced a fission event within the chamber by measuring the ionization signal using a segmented charge collector.

Chapter One : Ionization

Ionization is the liberation of an electron from the confines of an atom. The minimum amount of energy required to liberate the electron is referred to as the ionization energy. Energy transferred to the electron in excess of this ionization energy will appear in the form of the ejected electron's kinetic energy. Photons or charged particles like fission fragments interacting with a gas volume can induce ionization. The ionization process depends stochastically on the ionization cross section which is mainly affected by the fission fragment energy, type of the fission fragment (heavy or light), the gas pressure in the chamber, and the atomic properties of the gas. Generally, the amount of energy needed to have an ionization event in a gas is the same on average <ref name="Veenhof"> R. Veenhof, Internal Note/TPC, ALICE-INT-2003-29 version 1.0, 2003</ref>, regardless of the incident particle type or energy as shown in the following table for argon gas.

Type of particle and its energy	9 keV x-rays	10 keV electrons	40 keV electrons	x-rays Ar-37(K-capture)(5-25 keV) + beta	alpha 7.68 MeV	340 MeV protons
Energy per ion-electron pair (eV)	27.9 [math]\pm[/math] 1.5	27.3	25.4	27.0 [math]\pm[/math]0.5	26.25	25.5

Ionization by fission fragment is not the only source for a signal, but it is not the only ionization process, there are other physical processes occurs in the medium which are related to the gas mixture properties or the preamplifier material properties like: Photoionization, thermal ionization, deionization by attachment (negative ion formation) , photoelectric emission, electron emission by excited atoms or positive ion,and field emission <ref name="Kuffel"/>.

Choosing 90/10 Ar/CO2 gas mixture was not random. The behavior of the mixture is studied based on simulating the ionization in the gas mixture as it is in a gas chamber that has a wire cathode and an anode to produce a high electric field<ref name="Veenhof"/>. Garfield and Magboltz software packages were used for this purpose, Also Imonte 4.5 program can be for more precise simulation but it was not used for the simulations below <ref name="Veenhof"/>. The results of 90/10 ArCO2 simulation is summarized by the following:

Why 90/10 Ar/CO2 Mixture (Simulation by Garfield) <ref name="Veenhof"/>

• Drift velocity: Increasing the percentage of CO2 the gas mixture at low electric field increases the drift velocity as shown in the figure:

The drift velocity is saturated but at different values depending the percentage of the CO2, so the increase in the drift velocity becomes smaller withe increase in CO2 percentage int he gas mixture as show in the figures below:

• Gain: It is dependent on Townsend coefficient, the figure below shows the gain-Electric field relationship for different mixtures of ArCO2, in addition to the effect penning of the gain.

The figure above is not accurate enough since Garfield and Magboltz software packages use the first two terms of Legendre polynomials as solution for Boltzmann transport equation (Magboltz may extend to the third term when the simulation goes in the longer time one), but using using IMonte 4.5 uses the spherical harmonics which improved the simulation and make independent of the expansions that describe the electron energy distribution. <ref name="Biagi"> S.Biagi Nucl. Instrum. Methods, vol. A 421, pp. 234–240, 1999</ref >

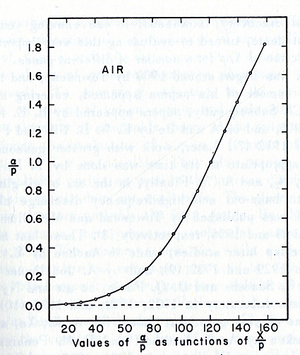
The effect of Penning on Townsend coefficient is represented by the following :

Comparing Ne/CO2 with Ar/CO2 considering the 40 percent of Penning transfer:

• Ionization rate:

• Attachment:

Diffusion

charged particle diffusion in gas is defined as <ref name="Mason"/> the "disperse" of the particles in a gas "in which there is a net spatial transport" of the charged particles "produced by the gradient in their relative concentrations". Assuming that the charged particles are localized in a gas with a uniform temperature, pressure and has low n charged particle density to ignore Coulomb force.

[math] J = -D \bigtriangledown n [/math]

where D is the diffusion coefficient and J is the number of the charged particle flow per unit time.

When a weak uniform electric field is applied, the charged particles will get a drift velocity directly proportional to the magnitude of the electric E and the proportionality constant is represented by 'K as in the following equation:

[math] v_{d} = K E[/math]

where K is the mobility of the charged particle.

The relationship between K and D exactly in limit of vanishing electric field and the ion concetration is represented by Einstein equation <ref name="Mason"/>:

[math] D = \frac{eD}{kT} [/math]

where e is the charge of charged particle and k is Boltzmann constant.

In case of the high electric field that the charged particle has an average velocity over a random motion affected by the high electric field and number of collisions with the gas atoms, then K is no longer a constant value and and the energy distribution does not follow Maxwell distribution, so the diffusion becomes a tensor and will be represented by the following equation:

\begin{vmatrix}
 D_{T}& 0 & 0 \\
 0, D_{T}& 0  \\
 0& 0 & D_{L}
\end{vmatrix}

where [math] D_T [/math] is the transverse diffusion and [math] D_L [/math] is the longitudinal diffusion to the direction of the electric field. It is worth to mention that Einstein equation mentioned above is not applied in this intermediate and high electric field.

Main differences between electrons and ions behavior in a gas <ref name="Mason">Mason, Edward A. and Earl W. MacDaniel. 1988. Transport Properties of Ions in Gases. John Wiley & Sons. </ref>

Haitham, here is a chance to get help with writing from the help center.  
Take the paragraph below to them and learn how to correct it.

H: Sure, but I need to add and edit some more to complete the idea then I will go there.

The ratio between the mass of the electrons and the gas atoms is very small, so with a few eV work done by the electric field, the electrons will gain a high velocity compared to that of the ions when are accelerated under the same electric field.

The probability of low energy electrons to make an interaction is higher that of the low energy ions supported by accurate calculations for the electron drift velocity. Electrons at low energy have the ability to produce vibrations and excitations in the gas atoms or molecules measured within the lab frame, but the low energy ions have a very low cross sections for the most of the interactions with the gas atoms or molecules, in addition to complexity in measuring the products of these interactions. Furthermore, the ratio between a gas atom or molecule is very small which simplify the calculations for the velocity distribution for the electrons in many gases.

Producing the electrons in a gas is simpler than producing ions in the same gas. a Large number of interactions appear in the gas for producing electrons like thermionic emission, photoemission, or a radioactive decay, but creating an ion requires electron bombardment, photo-ionization or an electric discharge which require more sophisticated conditions for the experiment , especially that the ions are not as sensitive as the electrons for the the non-uniformity of the electric field, electric potential and magnetic field.

The last difference that might be a concern in our case is the existence of the impurities. The electrons loses most of their energy in the molecular level compared to the electron energy loss within the atomic level for a pure gas. On the other hand, the ionic velocity distribution is not affected by the existence of these impurities except for some cases related to a highly accurate ionic studies in gases.

Gas Quenching

Rewrite the first two sentences so quenching is more clearly described.

Gas quenching is a non-ionizing process occurs when a gas molecules with large cross sections for excitation and vibration states decreases a charged particle energy to create any ionization when the charged particle passes through. Usually, the gas mixture ,contains the ionization event, consists mostly of gas atoms as a main source of electrons and the quenching gas, when the free electrons are scattered after the ionization, their energy is decreased by quenching so the number of secondary electrons becomes less, Consequently, a higher voltage is required to get a gain from this mixture than a medium only has a non-quenching gas<ref name="Sharma"> A.Sharma,F. Sauli, first Townsend coefficients measurements for argon gas european organization for nuclear research (1993) </ref >.

Not only does the quenching process decreases the electron energy, but also decreases the positive ions energy (produced by ionization) when the ions collide with these gas molecules and emits a photon or more from these positive ions. These photons represent the energy loss in a form other than the ionization which is called argon escape peak in case of using Argon gas.

Gas quenching experimentally can be measured by evaluating Townsend first coefficients A,B for different gas mixtures. The following table represents the Townsend first coefficients' values for different ratio of Ar/CO2 gas mixtures<ref name="Sharma"/>:

Percentage of CO2	3.7	22.8	87.2	100
A [math] cm^{-1}Torr^{-1} [/math]	5.04	221.1	158.3	145.1
B [math] Vcm^{-1}Torr^{-1} [/math]	90.82	207.6	291.8	318.2
[math] \frac{E}{p} \,\,\, Vcm^{-1}Torr^{-1} [/math]	16.2	21.6	32.9	36.4

The electric field pressure ratio in the last row is the upper limit of the reduced electric field which Townsend's equation fits considering E as a uniform electric field.

Townsend's Coefficients

Townsend's First Coefficient

Townsend's first Coefficient is defined as "the number of produced by an electron per unit length in the direction of the electric field"<ref name="Kuffel"/>.

• Townsend started his investigations about discharge after fundamental studies were known around 1899 about:

1- Conductivity production by x-rays.

2- Diffusion coefficients, mobility of ions and ion-electron recombinations.

• It was observed for an increment in Electric filed E and pressure P beyond the saturation current value, at some critical value of E and p, the current increases rapidly which will lead to a breakdown of the gap in the form of a spark <ref name="loeb"> L.B.Loeb, basics processes of gaseous electronics, University of California Press, 2nd edition, 1955. </ref>.

• Townsend studied the relationship between E/p as a function of x, where x is the separation distance between the plates. His study was based on the photoelectron emission from the cathode by ultraviolet light at high uniform electric field up to 30kV/cm and 1 atm pressure.

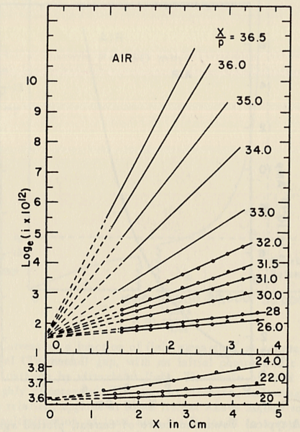
• He plotted different values for E/p, he found that the slope of the line is [math]\alpha[/math] which is "the number of the new electrons created by single electron in 1 cm path in the filed direction in a gas at appropriately high E/p" <ref name="loeb"/> . Townsend plotted [math] \frac{i}{i_0} [/math] against the distance of separation x, he concluded the following equation

[math] ln (\frac{i}{i_o}) = \alpha x [/math]

to calculate [math]\alpha[/math] (the slope) for different values of E/p as shown in the figure:

Fig. relationship between [math]ln{i}/{i_o}[/math] and the distance x for different values of E/p <ref name="loeb"/>

• Townsend studied [math]\alpha[/math] as a function of E/p for a given gas, he founded ,for different values of p,

[math]\alpha[/math] experimentally is different from expected value calculated, but the plots met in values when it represented the relationship between [math]\alpha[/math]/p as a function of E/p as shwon in the figure below.

Fig. shows alpha p ratio coincides with E p ratio <ref name="loeb"/>

• The relationship between [math]\alpha[/math]/p and E/p is shown below. However, the equation can not predict all the values of [math]\alpha[/math]/p accurately for different values of E/p, i.e having a single analytical function to fit the experimental results for a gas does not exist, because [math]\alpha[/math]/p is dependent on the number of electrons produced which changes as the average energy distribution of the ionizing electrons changes <ref name="loeb"/>.

[math] \frac {\alpha}{P}= Ae^{(\frac{-BP}{E})} [/math]

Theoretical evaluation of [math]\alpha/p[/math] as a function of E/p

• The first attempt was done by Townsend when the experimental data were limited by the to the high E/p.

Decreasing the discharge in THGEM

THEGM preamplifier is designed to be rebust, economical, and to get the maximum gain with the least discharge effect.

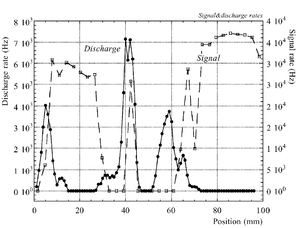
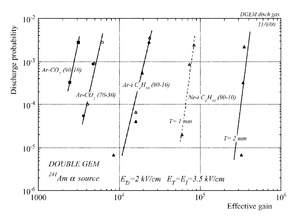
The discharge effect is when you experimentally start observing sparks coming from the detector. Whenever discharge becomes phenomenon to study then the probability of discharge is used. The probability of discharge is defined as the ratio between the observed frequency of the breakdown and source rate <ref name="bachmann"/>.The discharge rate and the source rate can be represented as function of position as shown in the figure.

Fig. Discharge rate and the detected source rate can be represented as function of position <ref name="bachmann"/>

Producing these sparks refers to many reasons,it is obviously observed when a highly ionizing ion passes through the gaseous chamber and produces enough free electrons to break down the rigidity of surrounding gas by having an avalanche size exceeds Raether limit ( [math] 10^7[/math] electron-ion pairs) when separating the electrodes vertically with small a distance <ref name="bachmann"> Bachmann et al NIM A 479 (2002) 294-308 </ref > .

Temperature, humidity, and gas flow externally affect the probability of the transition from the proportional multiplication to a discharge at a given potential, the effect clearly appears in absence of the amplification internal effects as the design quality and the history of the electrodes <ref name="bachmann"/>.

In case of heavily ionizing ions like alpha particles, an increase in gain causes the probability of discharge to increase, but the increment in the probability of discharge can be decreased by choosing an appropriate gap between the THGEM cards <ref name="bachmann"/>. As a result, achieving a maximum gain for an incident particle on a chamber with a specific gas mixture ,under a voltage applied on the THGEM cards, requires an appropriate distance that increases with increment of the ionization rate, i.e an alpha particle requires a bigger gap between the THGEM cards than that of a gamma ray to avoid the discharge effect.(can be experimentally proven).

Fig. Discharge probability as function of gain for double GEM detector <ref name="bachmann"/>

Boundary Element Method (BEM)

Boundary Element Method is used to solve Laplace or Poisson Equation, a function u(x,y,z) is solved on the domain boundary and the function partial derivatives are evaluated by integrating on the number of elements on the boundary.<ref name="Kuffel"> Kuffel, W. S. Zaengl, J. Kuffel, High voltage engineering: fundamentals, Biddle Ltd, 2nd edition, 2000 </ref>.

References

physical parameter	Effect on the detector properties <ref name="Veenhof"/>
Electron drift velocity	Dead time
Electron transverse diffusion	Spatial resolution (momentum resolution), transverse resolution should match the response function (signal width)
Townsend Coefficient	Gain which improves the resolution
Attachment Coefficient	Losing the information about an ionization, affects the position information and dE/dx identification
Gas breakdown	Discharge at that voltage
Ion mobility	Determine the rate of collecting the electrons (if the space charge is eliminated), the signal duration in the readout plate
Ionization rate	Affect the spatial resolution, dE/dx identification

<references/>