|
|
| Line 188: |
Line 188: |
| | </math> | | </math> |
| | | | |
| − | By changing quadrupole magnetic field strength $k$, we can change beam sizes <math>\sigma_{x,y}</math> on the screen. We make projection to the x, y axes, then fit them with Gaussian fittings to extract rms beam sizes, then plot vs <math>\sigma_{x,y}</math> vs <math>k_{1}L</math>. By Fitting a parabola we can find constants | + | By changing quadrupole magnetic field strength <math>k</math>, we can change beam sizes <math>\sigma_{x,y}</math> on the screen. We make projection to the x, y axes, then fit them with Gaussian fittings to extract rms beam sizes, then plot vs <math>\sigma_{x,y}</math> vs <math>k_{1}L</math>. By Fitting a parabola we can find constants |
| | <math>A</math>,<math>B</math>, and <math>C</math>, and get emittances. | | <math>A</math>,<math>B</math>, and <math>C</math>, and get emittances. |
| | | | |
Emittance
What is Emittance
In accelerator physics, Cartesian coordinate system was used to describe motion of the accelerated particles. Usually the z-axis of Cartesian coordinate system is set to be along the electron beam line as longitudinal beam direction. X-axis is set to be horizontal and perpendicular to the longitudinal direction, as one of the transverse beam direction. Y-axis is set to be vertical and perpendicular to the longitudinal direction, as another transverse beam direction.
For the convenience of representation, we use [math]z[/math] to represent our transverse coordinates, while discussing emittance. And we would like to express longitudinal beam direction with [math]s[/math]. Our transverse beam profile changes along the beam line, it makes [math]z[/math] is function of [math]s[/math], [math]z~(s)[/math]. The angle of a accelerated charge regarding the designed orbit can be defined as:
[math]z'=\frac{dz}{ds}[/math]
If we plot [math]z[/math] vs. [math]z'[/math], we will get an ellipse. The area of the ellipse is an invariant, which is called Courant-Snyder invariant. The transverse emittance [math]\epsilon[/math] of the beam is defined to be the area of the ellipse, which contains 90% of the particles <ref name="MConte08"> M. Conte and W. W. MacKay, “An Introduction To The Physics Of Particle Accelera
tors”, World Scientifc, Singapore, 2008, 2nd Edition, pp. 257-330. </ref>.
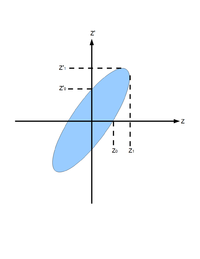
Fig.1 Phase space ellipse <ref name="MConte08"></ref>.
Measurement of Emittance with Quad Scanning Method
In quadrupole scan method, a quadrupole and a Yttrium Aluminum Garnet (YAG ) screen was used to measure emittance. Magnetic field strength of the quadrupole was changed in the process and corresponding beam shapes were observed on the screen.
Transfer matrix of a quadrupole magnet under thin lens approximation:
- [math]
\left( \begin{matrix} 1 & 0 \\ -k_{1}L & 1 \end{matrix} \right)=\left( \begin{matrix} 1 & 0 \\ -\frac{1}{f} & 1 \end{matrix} \right)
[/math]
Here, [math]k_{1} L[/math] is quadrupole strength, [math]L[/math] is quadrupole magnet thickness, and f is quadrupole
focal length. [math] k_{1} L \gt 0 [/math] for x-plane, and [math] k_{1} L \lt 0 [/math] for y-plane. Transfer matrix of a drift
space between quadrupole and screen:
- [math] \mathbf{S} = \left( \begin{matrix} S_{11} & S_{12} \\S_{21} & S_{22} \end{matrix} \right)=\left( \begin{matrix} 1 & l \\ 0 & 1 \end{matrix} \right)
[/math]
Here, [math]l[/math] ([math]S_{12}[/math]) is the distance from the center of the quadrupole to the screen.
Transfer matrix of the scanned region is:
[math]
\mathbf{M} =
\mathbf{SQ} =
\begin{pmatrix}
m_{11} & m_{12} \\
m_{21} & m_{22}
\end{pmatrix}=
\begin{pmatrix}
S_{11} & S_{12} \\
S_{21} & S_{22}
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
-k_1L & 1
\end{pmatrix}=
\begin{pmatrix}
S_{11} - k_1LS_{12} & S_{12} \\
S_{21} - k_1L S_{22} & S_{22}
\end{pmatrix}
[/math]
[math]\mathbf{M}[/math] is related with the beam matrix [math]\mathbf{\sigma}[/math] as:
[math]
\mathbf{ \sigma_{screen}} =
\mathbf{M \sigma_{quad} M^T} =
\begin{pmatrix}
m_{11} & m_{12} \\
m_{21} & m_{22}
\end{pmatrix}
\begin{pmatrix}
\sigma_{quad, 11} & \sigma_{quad, 12} \\
\sigma_{quad, 21} & \sigma_{quad, 22}
\end{pmatrix}
\begin{pmatrix}
m_{11} & m_{12} \\
m_{21} & m_{22}
\end{pmatrix}
[/math]
Since:
[math]
\sigma_{x}=\sqrt{\epsilon_x\beta},~\sigma_{x'}=\sqrt{\epsilon_x\gamma},~\sigma_{xx'}={-\epsilon_x\alpha}
[/math]
[math]
\mathbf{ \sigma} =
\begin{pmatrix}
\sigma_{11} & \sigma_{12} \\
\sigma_{21} & \sigma_{22}
\end{pmatrix} =
\begin{pmatrix}
\sigma_{x}^2 & \sigma_{xx'} \\
\sigma_{xx'} & \sigma_{x'}^2
\end{pmatrix}
[/math]
So, [math]\mathbf{\sigma}[/math] matrix can be written as:
[math]
\mathbf{\sigma}_{quad} =
\begin{pmatrix}
\sigma_{quad, x} & \sigma_{quad, xx'} \\
\sigma_{quad, xx'} & \sigma_{quad, x,}
\end{pmatrix} =
\epsilon_{rms, x}
\begin{pmatrix}
\beta & -\alpha \\
-\alpha & \gamma
\end{pmatrix}
[/math]
Substituting this give:
[math]
\mathbf{ \sigma_{screen}} =
\mathbf{M \sigma_{quad} M^T} =
\begin{pmatrix}
m_{11} & m_{12} \\
m_{21} & m_{22}
\end{pmatrix}
\epsilon_{rms, x}
\begin{pmatrix}
\beta & -\alpha \\
-\alpha & \gamma
\end{pmatrix}
\begin{pmatrix}
m_{11} & m_{12} \\
m_{21} & m_{22}
\end{pmatrix}
[/math]
Dropping off subscript "rms" on emittance [math]\epsilon_{rms, x}[/math]:
[math]
\sigma_{screen, 11}=\sigma_{screen, x}^2=\epsilon_x (m_{11}^2\beta - 2m_{12}m_{11}\alpha+m_{12}^2\gamma)
[/math]
Using [math]\mathbf{\sigma}[/math] matrix relations:
[math]
\sigma_{x}={\epsilon_x\beta},~\sigma_{12}={-\epsilon_x\alpha},~{\epsilon_x\gamma}=\epsilon_x \frac{1+\alpha^2}{\beta}=\frac{\epsilon_x^2+\sigma_{12}^2}{\sigma_{11}}
[/math]
Here [math]\sigma_{x}[/math] is [math]\sigma_{screen, x}[/math]. We got:
[math]
\sigma_{x}^2=m_{11}^2 \sigma_{11} + 2m_{12}m_{11} \sigma_{12} + m_{12}^2 \frac{\epsilon_x^2+\sigma_{12}^2}{\sigma_{11}}
[/math]
[math]
\sigma_{x}^2=\sigma_{11} \left(m_{11}^2 + 2m_{11}m_{12}\frac{\sigma_{12}}{\sigma_{11} }+ m_{12}^2\frac{\sigma_{12}^2}{\sigma_{11}^2}\right) + m_{12}\frac{\epsilon_x^2}{\sigma_{11}}
[/math]
[math]
\sigma_{x}^2=\sigma_{11}\left(m_{11} + m_{12}\frac{\sigma_{12}}{\sigma_{11} }\right)^2 + m_{12}\frac{\epsilon_x^2}{\sigma_{11}}
[/math]
Recall:
[math]
m_{11} = S_{11}-kLS_{12}~~~~~~m_{12}=S_{12}
[/math]
Substituting and reorganizing result in:
[math]
\sigma_{x}^2=\sigma_{11} {S_{12}^2}\left(kL - \left( \frac{S_{11}}{S_{12}} + \frac{\sigma_{12}}{\sigma_{11}} \right) \right)^2 + S_{12}^2\frac{\epsilon_x^2}{\sigma_{11}}
[/math]
Introducing constants [math]A[/math],[math]B[/math], and [math]C[/math]
[math]
A = \sigma_{11} {S_{12}^2},~~B = \frac{S_{11}}{S_{12}} + \frac{\sigma_{12}}{\sigma_{11}},~~C = S_{12}^2\frac{\epsilon_x^2}{\sigma_{11}}
[/math]
This will simplify equation to:
[math]
\sigma_{x}^2=A(kL - B)^2 + C = A(kL)^2 - 2AB(kL)+(C+AB^2)
[/math]
It is easy to see that:
[math]
\epsilon = \frac{\sqrt{AC}}{S_{12}^2}
[/math]
By changing quadrupole magnetic field strength [math]k[/math], we can change beam sizes [math]\sigma_{x,y}[/math] on the screen. We make projection to the x, y axes, then fit them with Gaussian fittings to extract rms beam sizes, then plot vs [math]\sigma_{x,y}[/math] vs [math]k_{1}L[/math]. By Fitting a parabola we can find constants
[math]A[/math],[math]B[/math], and [math]C[/math], and get emittances.
References
<references/>
Using APA reference style.
File:Emittance.tex
Go back: Positrons
