Sadiq Proposal Defense

Emittance

What is Emittance

In accelerator physics, Cartesian coordinate system was used to describe motion of the accelerated particles. Usually the z-axis of Cartesian coordinate system is set to be along the electron beam line as longitudinal beam direction. X-axis is set to be horizontal and perpendicular to the longitudinal direction, as one of the transverse beam direction. Y-axis is set to be vertical and perpendicular to the longitudinal direction, as another transverse beam direction.

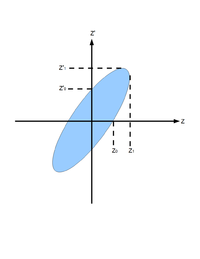
For the convenience of representation, we use [math]z[/math] to represent our transverse coordinates, while discussing emittance. And we would like to express longitudinal beam direction with [math]s[/math]. Our transverse beam profile changes along the beam line, it makes [math]z[/math] is function of [math]s[/math], [math]z~(s)[/math]. The angle of a accelerated charge regarding the designed orbit can be defined as:

[math]z'=\frac{dz}{ds}[/math]

If we plot [math]z[/math] vs. [math]z'[/math], we will get an ellipse. The area of the ellipse is an invariant, which is called Courant-Snyder invariant. The transverse emittance [math]\epsilon[/math] of the beam is defined to be the area of the ellipse, which contains 90% of the particles <ref name="MConte08"> M. Conte and W. W. MacKay, “An Introduction To The Physics Of Particle Accelera tors”, World Scientifc, Singapore, 2008, 2nd Edition, pp. 257-330. </ref>.

Fig.1 Phase space ellipse <ref name="MConte08"></ref>.

Measurement of Emittance with Quad Scanning Method

In quadrupole scan method, a quadrupole and a Yttrium Aluminum Garnet (YAG ) screen was used to measure emittance. Magnetic field strength of the quadrupole was changed in the process and corresponding beam shapes were observed on the screen. Transfer matrix of a quadrupole magnet under thin lens approximation:

[math] \left( \begin{matrix} 1 & 0 \\ -k_{1}L & 1 \end{matrix} \right)=\left( \begin{matrix} 1 & 0 \\ -\frac{1}{f} & 1 \end{matrix} \right) [/math]

Here, [math]k_{1} L[/math] is quadrupole strength, [math]L[/math] is quadrupole magnet thickness, and f is quadrupole focal length. [math] k_{1} L \gt 0 [/math] for x-plane, and [math] k_{1} L \lt 0 [/math] for y-plane. Transfer matrix of a drift space between quadrupole and screen:

S[math] = \left( \begin{matrix} S_{11} & S_{12} \\S_{21} & S_{22} \end{matrix} \right)=\left( \begin{matrix} 1 & l \\ -\frac{0}{1} & 1 \end{matrix} \right) [/math]

References

<references/>

Using APA reference style.

File:Emittance.tex

Go back: Positrons