GradFinalLab RS

Go Back to All Lab Reports

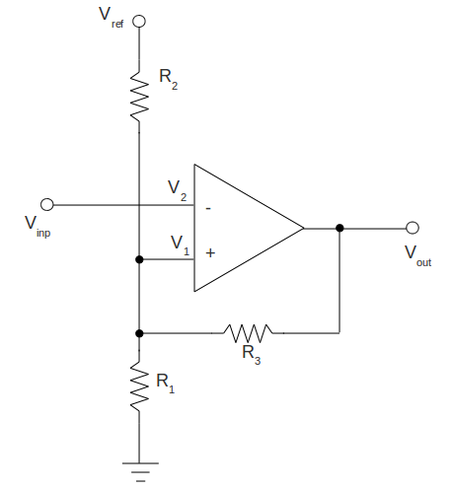
Construct a Schmitt Trigger using the 741 Op Amp

Draw the Schmitt Trigger circuit you constructed. Identify the values of all components

To construct the circuit above I am going to use the following components and voltages:

1. [math]R_1 = (1.01\pm0.01)\ k\Omega[/math]
2. [math]R_2 = (1.01\pm0.01)\ k\Omega[/math]
3. [math]R_3 = (5.10\pm0.01)\ k\Omega[/math]
4. [math]\mbox{OP}\ \mbox{AMP}\ 741[/math]
5. [math]V_{ref} = (+11.90\pm0.01)\ V[/math]
6. [math]V_{cc} = (+11.90\pm0.01)\ V[/math]
7. [math]V_{ee} = (-12.11\pm0.01)\ V[/math]

Identify the input voltage threshold levels at which a [math] V_{in}[/math] will produce [math]V_{out} \approx V_{cc}[/math]

The theory does say (ch. 10.19 The Schmitt Trigger R. Simpson "Introductory electronics for scientists and engineers"):

[math]V_2 = \frac{R_{123}}{R_2}V_{ref} + \frac{R_{123}}{R_3}V_{out}[/math]

1) if the output is high:

[math]V_2 = \frac{R_{123}}{R_2}V_{ref} + \frac{R_{123}}{R_3}V_{out_1}[/math]

2) if the output is low:

[math]V_2^' = \frac{R_{123}}{R_2}V_{ref} - \frac{R_{123}}{R_3}V_{out_1}[/math]

where

[math]R_{123} = (R_1 || R_2 || R_3) = \frac{R_1 R_2 R_3}{R_1+R_2+R_3}[/math]

and [math]V_{out_1}[/math] and [math]V_{out_2}[/math] approximately equal to supply voltage [math]V_{cc}[/math]

The actual measured values of high and low output voltages (they do not really equal to [math]\pm V_{cc}[/math]) are:

1. [math]V_{out_1} = (+11.06\pm0.01)\ V[/math]
2. [math]V_{out_2} = (-10.54\pm0.01)\ V[/math]

Substituting all quantities in the formulas above:

[math]R_{123} = (1.01\pm 0.01)\ k\Omega || (1.01\pm 0.01)\ k\Omega || (5.10\pm 0.05)\ k\Omega = (0.459\pm 0.003)\ k\Omega[/math]

[math]V_2 = \frac{(0.459\pm 0.003)\ k\Omega}{(1.01\pm 0.01)\ k\Omega}(11.90\pm 0.01)\ V + \frac{(0.459\pm 0.003)\ k\Omega}{(5.10\pm 0.05)\ k\Omega}(11.06\pm 0.01)\ V[/math]

[math]V_2^' = \frac{(0.459\pm 0.003)\ k\Omega}{(1.01\pm 0.01)\ k\Omega}(11.90\pm 0.01)\ V - \frac{(0.459\pm 0.003)\ k\Omega}{(5.10\pm 0.05)\ k\Omega}(10.54\pm0.01)\ V[/math]

and doing math and propagating errors we end up with the following predicted threshold voltages:

1) If the output voltage is high the threshold voltage are:

<math>V_2 = (6.41\pm 0.07)\ V 

1) If the output voltage is low the threshold voltage are:

<math>V_2 = (4.46\pm 0.06)\ V

Compare the threshold values to what is expected.

Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement