Lab 14 RS

Go Back to All Lab Reports

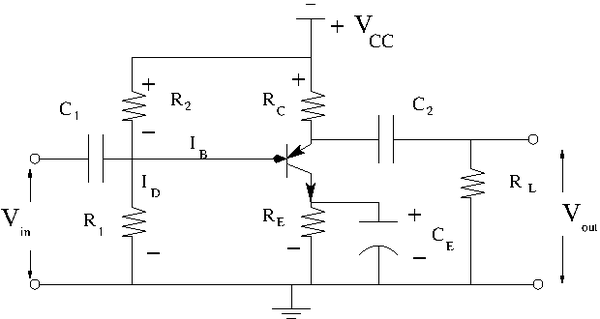
The Common Emitter Amplifier

Circuit

Construct the common emitter amplifier circuit below according to your type of emitter.

Calculate all the R and C values to use in the circuit such that

a. Try [math]R_B \approx 220 \Omega[/math] and [math]I_C \approx 100 \mu A[/math]

b. [math]I_C \gt 0.5[/math] mA DC with no input signal

c. [math]V_{CE} \approx V_{CC}/2 \gt 2[/math] V

d. [math]V_{CC} \lt V_{CE}(max)[/math] to prevent burnout

e. [math]V_{BE} \approx 0.6 V[/math]

f. [math]I_D \approx 10 I_B \lt 1[/math] mA

Let's [math]V_{CC} = 11\ V[/math], [math]R_E = 0.2\ k\Omega[/math] and [math]R_C = 2.0\ k\Omega[/math].

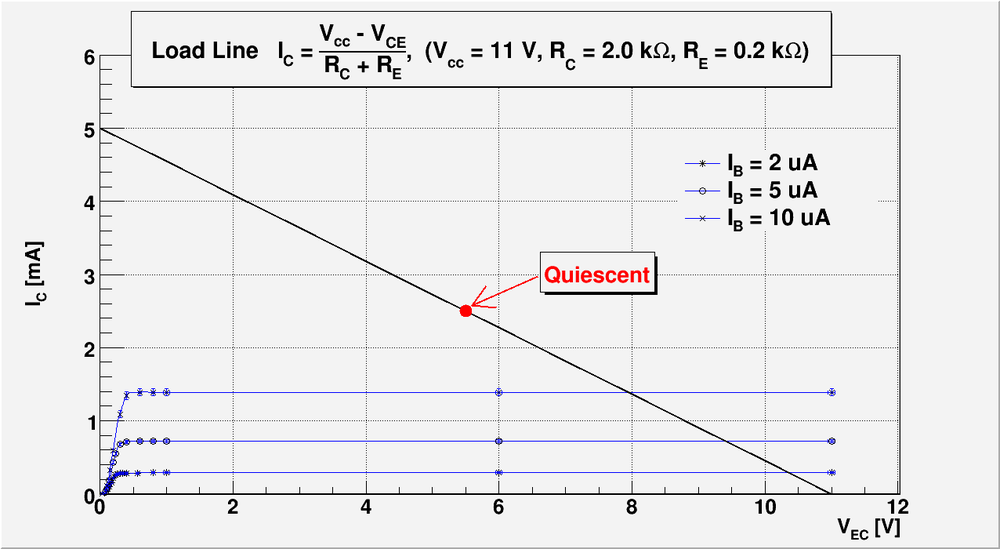
The load line equation becomes:

[math]I_C = \frac{V_{CC}-V_{CE}}{R_E+R_C} = \frac{(11 - V_{CE})\ V}{2.2\ k\Omega} [/math]

Draw a load line using the [math]I_{C}[/math] -vs- [math]I_{EC}[/math] from the previous lab 13. Record the value of [math]h_{FE}[/math] or [math]\beta[/math].

On the plot below I overlay the output transistor lines (from the previous lab report #13) and the Load Line calculated above.

My [math]\beta \approx 170[/math] based on my previous lab report #13

Set a DC operating point [math]I^{\prime}_C[/math] so it will amplify the input pulse given to you. Some of you will have sinusoidal pulses others will have positive or negative only pulses.

I will set up my operating point in the middle of the load line: [math]I_C = 2.5\ mA[/math], [math]V_EC = 5.5\ V[/math].

Let's calculate all bias voltage needed to set up this operating point. Because the knowing of [math]V_{BE}[/math] and [math]/beta[/math] is very important for this calculation I did the preliminary set up to measure this quantities. They are the only parameters which depends from transistor. I was able to find:

[math]V_{BE} = 0.68\ V[/math]
[math]/beta = 173[/math]

Now

[math]V_E = I_E \cdot R_E = 2.5\ mA \cdot 0.2\ k\Omega = 0.5\ V[/math]
[math]V_B = V_E + V_B = (0.50 + 0.68)\ V = 1.18\ V[/math]

To set up the operating point above we need to set up [math]V_{B} = 1.18\ V[/math].

We have:

[math]I_B = \frac{I_C}{\beta} = \frac{2.5\ mA}{173} = 14.4\ uA[/math].

To get operating point independent of the transistor base current we want [math]I_{R1} \gg\ I_B[/math]

Let's [math]I_{R1} = 590\ uA \gg\ I_B = 14.4\ uA[/math]

So

[math]R_1 = \frac{V_B}{I_1} = \frac{1.18\ V}{590\ uA} = 2\ k\Omega[/math]

And [math]R_2[/math] we can find from Kirchhoff voltage Low:

[math]V_{CC} = I_2 \cdot R_2 + V_B[/math]. And [math]I_2 = I_1 + I_B[/math]

So

 [math]R_2 = \frac{V_{CC}-V_B}{I_1+I_B} = \frac{(11-1.18)\ V}{(590 + 14.4)\ mA} = 16.25\ k\Omega[/math]

Measure all DC voltages in the circuit and compare with the predicted values.(10 pnts)

My predicted DC voltage are:

We have from operating point:

[math]V_{EC} = 10\ V[/math] 
[math]I_C \approx I_E = 5\ mA[/math]

And because we have silicon transistor:

[math]V_{BE} = 0.6\ V [/math]

Now

[math]V_E = I_E \cdot R_E = 5\ mA \cdot 200\ \Omega = 1\ V[/math]
[math]V_C = V_E + V_{EC} = (1 + 11)\ V = 12\ V[/math]
[math]V_B = V_E + V_{BE} = (1 + 0.6)\ V = 1.6\ V[/math]

My measured DC voltage are:

[math]V_{EC} = (11.25 \pm 0.01)\ V[/math]
[math]V_{BE} = (0.69 \pm 0.01)\ V [/math]

[math]V_E = (0.88 \pm 0.01)\ V[/math]
[math]V_C = (12.11 \pm 0.01)\ V[/math]
[math]V_B = (1.56 \pm 0.01)\ V[/math]

First note that my [math]V_B = (1.56 \pm 0.01)\ V[/math] is close to predicted values [math]V_B = 1.6\ V[/math].

Also note that my [math]V_{EC} = (11.25 \pm 0.01)\ V[/math] is a little higher than my initial operating point [math]V_{EC} = 10\ V[/math]. The main reason is that my actual values of [math]V_{BE} = (0.69 \pm 0.01)\ V [/math] instead of [math]V_{BE} = 0.6\ V [/math] as I was assumed initially. That will reduce my [math]V_E[/math] voltage that reduce my [math]I_C[/math] current. So I will shift to right my operating point from [math]I_C = 5\ mA[/math] to lower values and correspondingly will increase my [math]V_{EC}[/math].

By direct measurements my operating point now is [math]I_C = (4.34 \pm 0.01)\ mA[/math] and [math]V_{EC} = (11.25 \pm 0.01)\ V[/math]

Let's check do my operating point is still on my load line. I have [math]R_E = (0.20 \pm 0.01)\ k\Omega[/math], [math]R_C = (1.80 \pm 0.01)\ k\Omega[/math]. So from load line equation:

[math]I_C = \frac{V_{CC}-V_{CE}}{R_E+R_C} = \frac{((20.01\pm 0.01)-(11.25\pm 0.01))\ V}{((1.80 \pm 0.01))+ (0.20 \pm 0.01))\ k\Omega} = (4.38 \pm 0.04)\ mA[/math].

So my operating point lies in my load line within experimental error.

Measure [math]R_{in}[/math] and [math]R_{out}[/math] at about 1 kHz and compare to the theoretical value.(10 pnts)

How do you do this? Add resistor in front of [math]C_1[/math] which you vary to determine [math]R_{in}[/math] and then do a similar thing for [math]R_{out}[/math] except the variable reistor goes from [math]C_2[/math] to ground.

Questions

1. Why does a flat load line produce a high voltage gain and a steep load line a high current gain? (10 pnts)
2. What would be a good operating point an an [math]npn[/math] common emitter amplifier used to amplify negative pulses?(10 pnts)
3. What will the values of [math]V_C[/math], [math]V_E[/math] , and [math]I_C[/math] be if the transistor burns out resulting in infinite resistance. Check with measurement.(10 pnts)
4. What will the values of [math]V_C[/math], [math]V_E[/math] , and [math]I_C[/math] be if the transistor burns out resulting in near ZERO resistance (ie short). Check with measurement.(10 pnts)
5. Predict the change in the value of [math]R_{in}[/math] if [math]I_D[/math] is increased from 10 [math]I_B[/math] to 50 [math]I_B[/math](10 pnts)
6. Sketch the AC equivalent circuit of the common emitter amplifier.(10 pnts)

Go Back to All Lab Reports Forest_Electronic_Instrumentation_and_Measurement