Difference between revisions of "TF EIM Chapt3"
| Line 30: | Line 30: | ||
|<math> RC << \tau</math> || <math>RC >> \tau</math> | |<math> RC << \tau</math> || <math>RC >> \tau</math> | ||
|} | |} | ||
| + | |||
| + | == Loop Theorem== | ||
| + | |||
| + | :<math>V_{in} = V_C + V_R = I X_C + I R</math> | ||
| + | |||
| + | |||
| + | ;How does <math>V_C</math> compare to <math>V_R</math> ? | ||
| + | |||
| + | :<math>\left | \frac{V_R}{V_C} \right | = \frac{\left | IR \right |}{\left | I X_C\right |}= \frac{R}{\left | \frac{1}{i \omega C}\right |}</math> | ||
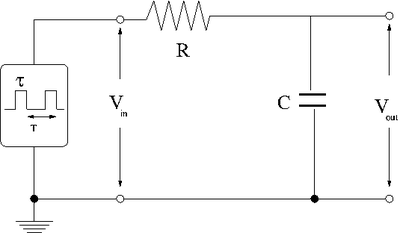
=Integrator= | =Integrator= | ||
Revision as of 18:43, 8 February 2011
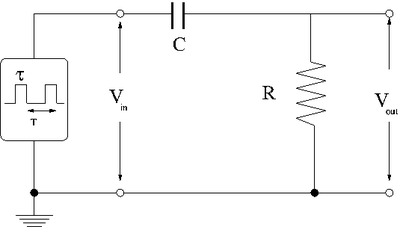
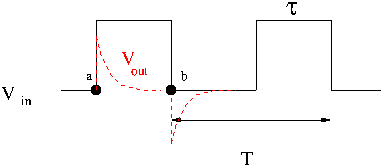
Differentiator circuit
Consider the effect of a low-pass filter on a rectangular shaped input pulse with a width and period .
The first thing to consider is what happens to the different parts of the square pulse as it travels to the circuit.
You know that the circuit, as a high pass filter, will tend to attenuate low frequency (slow changing) voltages and not high frequency (quick changing) voltages.
This means no DC voltage values pass beyond the capacitor.
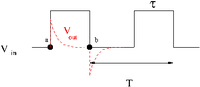
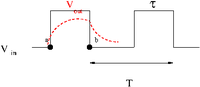
This means that points and in the pulse shown below should pass through the circuit.
The voltage changes in between point and DC are passed according to what you select for the break frequency ()
In the above pulse picture it was assumed that or in other words the RC network time constant is a lot smaller than the pulse width.
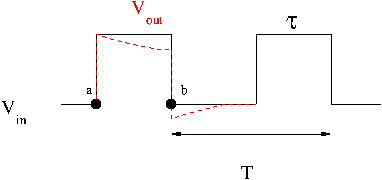
If the RC time constant is larger than the pulse width then you will see the voltage stay high. The rectangular pulse will be output as a square like pulse which is "sagging".
 |
|
Loop Theorem
- How does compare to ?