Difference between revisions of "Lab 5 RS"

From New IAC Wiki
Jump to navigation Jump to search
Line 5: Line 5:
 
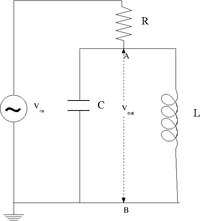
=The LC cicuit=
 
=The LC cicuit=
 
[[File:TF_EIM_Lab5_LC.png| 200 px]]
 
[[File:TF_EIM_Lab5_LC.png| 200 px]]
−
#Design a '''parallel''' LC resonant circuit with a resonant frequency between 50-200 kHz.  use <math>L</math> = 10 - 100 <math>\mu H</math>.
+
==Design a '''parallel''' LC resonant circuit with a resonant frequency between 50-200 kHz.  use <math>L</math> = 10 - 100 <math>\mu H</math>.==
  
 
  <math>\omega_0=\frac{1}{\sqrt{\mbox{LC}}}</math>
 
  <math>\omega_0=\frac{1}{\sqrt{\mbox{LC}}}</math>
  
−
#Construct the LC circuit using a non-polar capacitor
+
==Construct the LC circuit using a non-polar capacitor==
−
#Measure the Gain <math>\equiv \frac{V_{out}}{V_{in}}</math> as a function of frequency. (20 pnts)
+
==Measure the Gain <math>\equiv \frac{V_{out}}{V_{in}}</math> as a function of frequency. (20 pnts)==
−
#Measure the Gain when an external resistance approximately equals to the inherent resistance of the rf choke <math>R_{L}</math>. (20 pnts)
+
==Measure the Gain when an external resistance approximately equals to the inherent resistance of the rf choke <math>R_{L}</math>. (20 pnts)==
−
#Compare the measured and theoretical values from the resonance frequency (<math>\omega_{L}</math>) and the Quality factor <math>Q \equiv 2 \pi \frac{W_S}{W_L} = 2 \pi \frac{\mbox{Energy Stored}}{\mbox{Energy Lost}}</math> value for each case; <math>W = \frac{1}{2}LI^2</math>. (10 pnts)
+
==Compare the measured and theoretical values from the resonance frequency (<math>\omega_{L}</math>) and the Quality factor <math>Q \equiv 2 \pi \frac{W_S}{W_L} = 2 \pi \frac{\mbox{Energy Stored}}{\mbox{Energy Lost}}</math> value for each case; <math>W = \frac{1}{2}LI^2</math>. (10 pnts)==
  
 
==Questions==
 
==Questions==

Revision as of 04:51, 1 February 2011

Go Back to All Lab Reports


LC Resonance circuits

The LC cicuit

TF EIM Lab5 LC.png

Design a parallel LC resonant circuit with a resonant frequency between 50-200 kHz. use [math]L[/math] = 10 - 100 [math]\mu H[/math].

[math]\omega_0=\frac{1}{\sqrt{\mbox{LC}}}[/math]

Construct the LC circuit using a non-polar capacitor

Measure the Gain [math]\equiv \frac{V_{out}}{V_{in}}[/math] as a function of frequency. (20 pnts)

Measure the Gain when an external resistance approximately equals to the inherent resistance of the rf choke [math]R_{L}[/math]. (20 pnts)

Compare the measured and theoretical values from the resonance frequency ([math]\omega_{L}[/math]) and the Quality factor [math]Q \equiv 2 \pi \frac{W_S}{W_L} = 2 \pi \frac{\mbox{Energy Stored}}{\mbox{Energy Lost}}[/math] value for each case; [math]W = \frac{1}{2}LI^2[/math]. (10 pnts)

Questions

  1. If r=0, show that [math]Q = \frac{1}{\omega_0 R_L C}[/math]. (10 pnts)
  2. Show that at resonance[math] Z_{AB} \approx Q \omega_0 L[/math]. (10 pnts)

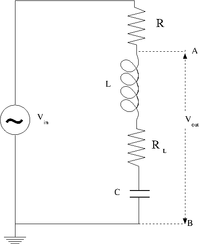
The LRC cicuit

TF EIM Lab5 RLC.png

  1. Design and construct a series LRC circuit.
  2. Measure and Graph the Gain as a function of the oscillating input voltage frequency. (20 pnts)

Questions

  1. What is the current [math]I[/math] at resonance? (5 pnts)
  2. What is the current as [math]\nu \rightarrow \infty[/math]? (5 pnts)


Forest_Electronic_Instrumentation_and_Measurement Go Back to All Lab Reports

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Lab_5_RS&oldid=56157"