Difference between revisions of "Lab 3 RS"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
= 1-50 kHz filter (20 pnts)= | = 1-50 kHz filter (20 pnts)= | ||
| − | + | ==Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed)== | |
:To design low-pass RC filter I had: | :To design low-pass RC filter I had: | ||
| Line 16: | Line 16: | ||
| − | + | ==Now construct the circuit using a non-polar capacitor== | |
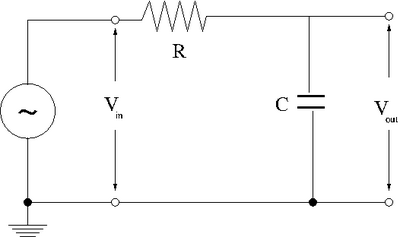
[[File:TF_EIM_Lab3.png | 400 px]] | [[File:TF_EIM_Lab3.png | 400 px]] | ||
| − | + | ==Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter== | |
| − | + | ==Measure the input <math>(V_{in})</math> and output <math>(V_{out})</math> voltages for at least 8 different frequencies<math> (\nu)</math> which span the frequency range from 1 Hz to 1 MHz== | |
{| border="1" cellpadding="12" cellspacing="0" | {| border="1" cellpadding="12" cellspacing="0" | ||
| Line 61: | Line 61: | ||
|} | |} | ||
| − | + | ==Graph the <math>\log \left(\frac{V_{out}}{V_{in}} \right)</math> -vs- <math>\log (\nu)</math>== | |
Revision as of 02:41, 26 January 2011
- RC Low-pass filter
1-50 kHz filter (20 pnts)
Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed)
- To design low-pass RC filter I had:
Now construct the circuit using a non-polar capacitor
Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter
Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz
| 0.1 | 5.0 | 5.0 | 1.0 | ||
| 1.0 | 4.2 | 4.2 | 1.0 | 14.0 | 0.094 |
| 2.0 | 3.2 | 3.1 | 0.97 | 14.0 | 0.188 |
| 5.0 | 1.8 | 1.6 | 0.89 | 14.0 | 0.471 |
| 10.0 | 1.14 | 0.88 | 0.77 | 11.0 | 0.628 |
| 16.7 | 0.90 | 0.54 | 0.60 | 8.5 | 1.049 |
| 20.0 | 0.88 | 0.48 | 0.54 | 8.0 | 1.005 |
| 25.0 | 0.82 | 0.38 | 0.46 | 7.0 | 1.099 |
| 33.3 | 0.78 | 0.28 | 0.36 | 6.0 | 1.255 |
| 50.0 | 0.76 | 0.18 | 0.24 | 4.5 | 1.413 |
| 100.0 | 0.75 | 0.09 | 0.12 | 2.0 | 1.256 |
| 125.0 | 0.74 | 0.07 | 0.095 | 1.8 | 1.413 |
| 200.0 | 0.75 | 0.04 | 0.053 | 0.9 | 1.005 |
| 333.3 | 0.76 | 0.03 | 0.039 | 0.25 | 0.523 |
| 200.0 | 0.76 | 0.03 | 0.039 | -0.25 | -0.785 |
| 1000.0 | 0.78 | 0.06 | 0.077 | -0.25 | -1.570 |
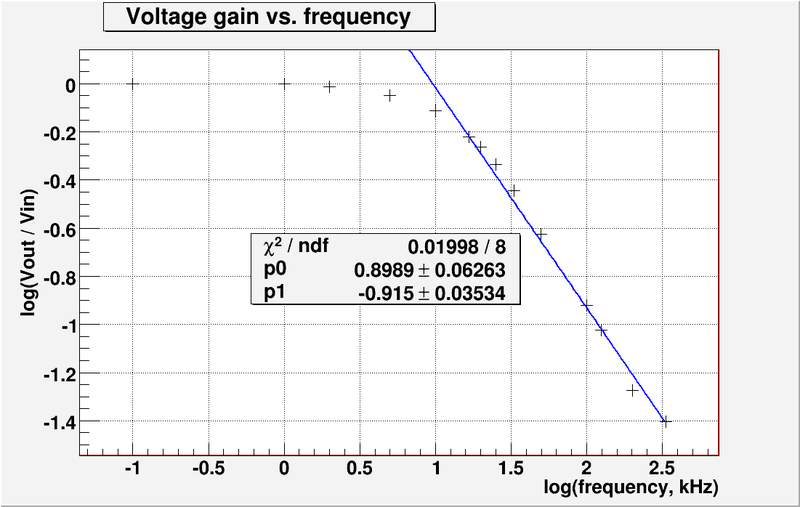
Graph the -vs-
phase shift (10 pnts)
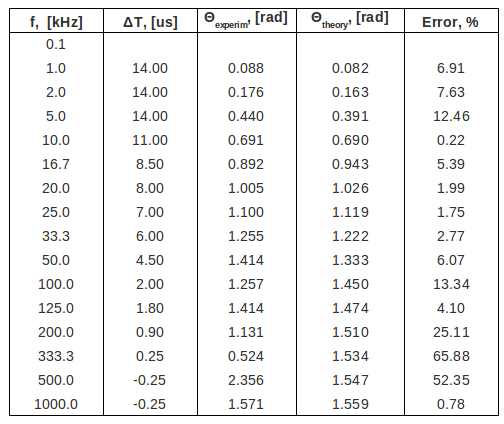
- measure the phase shift between and as a function of frequency . Hint: you could use as an external trigger and measure the time until reaches a max on the scope .
See table above, columns #5 and #6.
Questions
1. Compare the theoretical and experimentally measured break frequencies. (5 pnts)
method 1. Using fitting line
- Theoretical break frequency: 12.1 kHz
- Experimentally measured break frequency: 9.59 kHz
Q: The above was read off the graph? Why not use fit results? A: The fit was made by using GIMP Image Editor. I do not have so much experience with ROOT. But I will try to do it. Thank you for comment. A1: The fit was done by ROOT
- The fit line equation from the plot above is .
- From intersection point of line with x-axis we find:
- The error is:
method 2. Using the -3 dB point
At the break point the voltage gain is down by 3 dB relative to the gain of unity at zero frequency. So the value of . Using this value I found from plot above . So . The error in this case is 4.1 %.
2. Calculate and expression for as a function of , , and . The Gain is defined as the ratio of to .(5 pnts)
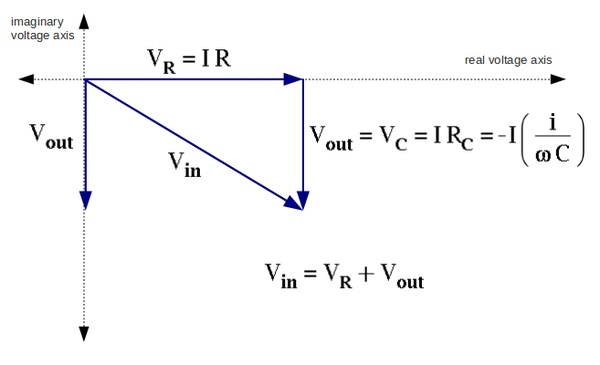
We have:
Dividing second equation into first one we get the voltage gain:
And we are need the real part:
3. Sketch the phasor diagram for ,, , and . Put the current along the real voltage axis. (30 pnts)
4. Compare the theoretical and experimental value for the phase shift . (5 pnts)
The experimental phase shift is
The theoretical phase shift is