Lab 3 RS

Go Back to All Lab Reports

RC Low-pass filter

1-50 kHz filter (20 pnts)

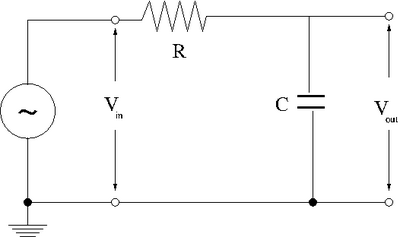
1. Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed).

To design low-pass RC filter I had:

[math]R=10.5\ \Omega[/math]
[math]R=1.250\ \mu F[/math]
[math]\omega_b = \frac{1}{RC} = 76.2\ kHz[/math]

2. Now construct the circuit using a non-polar capacitor.

3. Use a sinusoidal variable frequency oscillator to provide an input voltage to your filter.

4. Measure the input [math](V_{in})[/math] and output [math](V_{out})[/math] voltages for at least 8 different frequencies[math] (\nu)[/math] which span the frequency range from 1 Hz to 1 MHz.

[math]\nu[/math]	[math]V_{in}[/math]	[math]V_{out}[/math]	[math]\frac{V_{out}}{V_{in}}[/math]
Hz	Volts	Volts

5. Graph the [math]\log \left(\frac{V_{out}}{V_{in}} \right)[/math] -vs- [math]\log (\nu)[/math]

phase shift (10 pnts)

1. measure the phase shift between [math]V_{in}[/math] and [math]V_{out}[/math] as a function of frequency [math]\nu[/math]. Hint: you could use [math] V_{in}[/math] as an external trigger and measure the time until [math]V_{out}[/math] reaches a max on the scope [math](\sin(\omega t + \phi) = \sin\left ( \omega\left [t + \frac{\phi}{\omega}\right]\right )= \sin\left ( \omega\left [t + \delta t \right] \right ))[/math].

Questions

1. compare the theoretical and experimentally measured break frequencies. (5 pnts)
2. Calculate and expression for [math]\frac{V_{out}}{ V_{in}}[/math] as a function of [math]\nu[/math], [math]R[/math], and [math]C[/math]. The Gain is defined as the ratio of [math]V_{out}[/math] to [math]V_{in}[/math].(5 pnts)
3. Sketch the phasor diagram for [math]V_{in}[/math],[math] V_{out}[/math], [math]V_{R}[/math], and [math]V_{C}[/math]. Put the current [math]I[/math] along the real voltage axis. (30 pnts)
4. Compare the theoretical and experimental value for the phase shift [math]\theta[/math]. (5 pnts)
5. what is the phase shift [math]\theta[/math] for a DC input and a very-high frequency input?(5 pnts)
6. calculate and expression for the phase shift [math]\theta[/math] as a function of [math]\nu[/math], [math]R[/math], [math]C[/math] and graph [math]\theta[/math] -vs [math]\nu[/math]. (20 pnts)

Forest_Electronic_Instrumentation_and_Measurement

Go Back to All Lab Reports