TF EIM Chapt2

Alternating Current (AC)

Thus far we have discussed direct current circuits which were built from a battery (constant voltage supply).

Another type of circuit is one in which the current is driven in an alternating fashion. Typically the current is increased so some positive maximum value, then decreased until it passes through zero and reverses direction until it reaches another maximum value and then it is decreased again, passing though zero once more on its way to a positive maximum value.

Definitions

frequency ([math]f[/math], [math]\nu[/math] )

The frequency is number of complete cycles which occur in 1 sec (cycles/sec = Hz)

Angular frequency =[math] \omega = 2\pi f[/math] = radians/sec

Period

The period is the time to complete one cycle = 1/[math]f[/math]

Amplitude

The change in the current from zero to its most positive value

peak-to-peak

The amount the current changes from its largest positive value to its most negative.

phase

The time a current takes to reaches its maximum value compared to another alternating current

Note

The above definitions can be used for voltage as easily as current.

Mathematical description

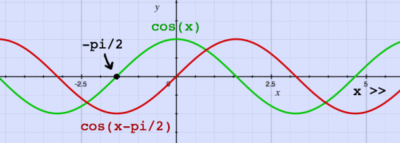
Trigonometric

[math]I(t) = \sin(\omega t + \phi) = \cos(\omega t + \phi - \pi/2)[/math]

Note

A 180 degree ([math]\pi[/math] radian) phase shift will put the above cosine wave completely out of sync with the original one such that if we add the two signals together the net current would be zero.

I_{RMS}

With this functional form for the alternating current we can now calculate another property, the RMS or root mean square.

The RMS quantifies an average fluctuation of the alternating current such that

[math]I_{RMS} \equiv \sqrt{\frac{1}{T} \int_0^T I^2(t) dt} = \sqrt{\frac{1}{T} \int_0^T I_0^2 \sin^2(\omega t) dt}= \frac{I_0}{\sqrt{2}} [/math]

where T represent the time interval over which the average is calculated ([math]\infty[/math])

[math]\int_0^T \sin^2(x) dx = \int_0^T \frac{1}{2} \left (1 - \cos(2x) \right) dx = \frac{1}{2} + \frac{1}{T} \int_0^T \cos(t)dt = \frac{1}{2}[/math] if T is infinite or an integer number of cycles

Power

The instantaneous power dissipated in a resister by an alternating current is given as

[math]P_{inst}(t) =I^2(t) R = R\sin^2(\omega t)[/math]

Average power

[math]P_{ave} = \frac{1}{T} \int_0^T P(t) dt = \frac{1}{T} \int_0^T RI^2(t) dt = \frac{R}{T} \int_0^T \sin^2(\omega t) dt = \frac{I_0^2R}{\sqrt{2}} = I_{RMS}^2 R[/math]

Plane waves

Another mathematical expression for an alternating current uses complex variables

[math]I=I_0 \exp^{i \left ( \omega t \right )} = I_0 \left ( \cos \left ( \omega t \right) + i \sin \left ( \omega t \right) \right )[/math]

as an aside; a plane wave in space is given as

[math]I=I_0 \exp^{i \left ( kx -\omega t \right )} = I_0 \left ( \cos \left ( kx -\omega t \right) + i \sin \left ( kx -\omega t \right) \right )[/math]

to determine the direction of the wave let

[math] kx-\omega t = 0 \Rightarrow x= \omega t /k = v_{group} t \Rightarrow[/math] wave moving in the +x direction

Voltage sources of AC current

The circuit symbol for an emf used to drive alternating currents is given below

The mathematic form is

[math]V = V_0 \sin(\omega t)[/math]