Minimum accelerator energy to run experiment

Go Back

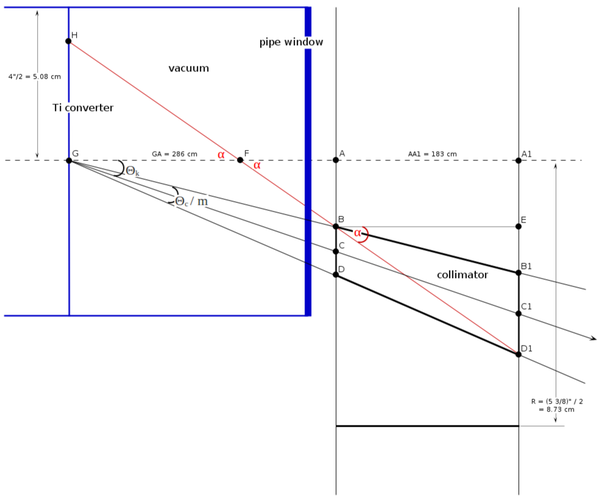
general setup

fitting the collimator size into the hole in the concrete wall

I can express the distance [math]A_1D_1[/math] as function of collimator size [math]\Theta_C/m[/math] and electron beam energy E:

[math]A_1D_1(E,\ \Theta_C/m) = \frac{469}{2}\tan(\frac{0.511}{E}) + \frac{469}{sqrt{2}}\tan(\frac{1}{m}\frac{0.511}{E})\lt \math\gt 

The minimum energy of accelerator (MeV) is limited by fitting the collimator size \lt math\gt r_2[/math] into the hole R = 8.73 cm:

[math]x_2 + r_2 = R[/math]

1) Assuming the collimator diameter is [math]\Theta_C[/math]:

[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
       \frac{1}{2}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 33.1\ MeV  [/math]

2) Assuming the collimator diameter is [math]\Theta_C/2[/math]:

[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
       \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{2}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 26.3\ MeV  [/math]

3) Assuming the collimator diameter is [math]\Theta_C/4[/math]:

[math]\frac{1}{\sqrt{2}}\ (286+183)\ \tan\left(\frac{0.511}{E_{min}}\right) +
       \frac{1}{2}\ (286+183)\ \tan\left(\frac{1}{4}\ \frac{0.511}{E_{min}}\right) = 8.73 \Rightarrow E_{min} = 22.8\ MeV  [/math]

4) for arbitrary collimator size [math]\Theta_C/2[/math]:

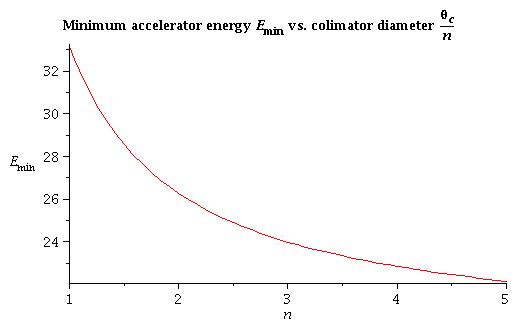
All energy under this line is good to run experiment for condition above

GH = 5.08 cm condition

1) assuming the collimator diameter is [math]\Theta_C[/math]

[math] E_{min} = 73.7\ MeV  [/math]

2) assuming the collimator diameter is [math]\Theta_C/2[/math]

[math] E_{min} = 36.9\ MeV  [/math]

3) assuming the collimator diameter is [math]\Theta_C/4[/math]

[math] E_{min} = 18.4\ MeV  [/math]

4) for arbitrary collimator size [math]\Theta_C/m[/math]:

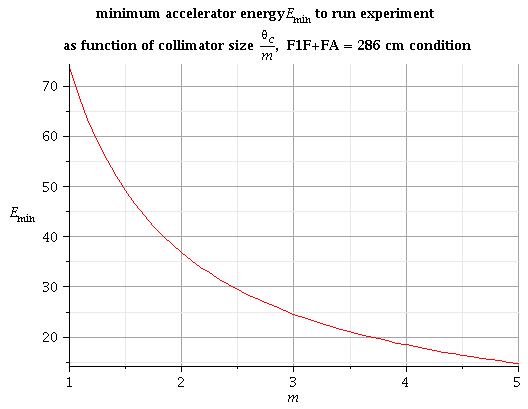
All energy under this line is good to run experiment for condition above

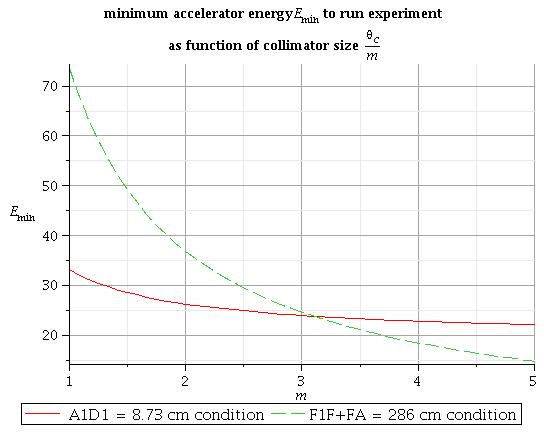
both conditions above are together

All energy under this linse is good to run experiment for both conditions above

Go Back