Revision as of 07:06, 8 June 2010

The first version of a positron converter target will be designed to distribute the heat load by rotating the tungsten target.

Calculate for 1 mm and 2 mm thick Tungsten

Look for Tungsten disks to attach to brushless motor and fit into beam pipe

Properties of Tungsten

Melting Point = 3695 K.

Heat Capacity =

These data are from: Tungsten

Heat loss due to radiation: ( \sigma T^4)

Tungsten Temperature as a function of heat load

IAC beamline pressure = [math]10^{-8} [/math] Torr

The Tungsten heats up when an MeV energy electron impinges its surface. The imperfect vacuum inside the beam pipe does allow some radiative cooling.

Conduction and Radiation

Calculating Radiators Equilibrium Temperature

1.Calculating number of particles per second

We have electron beam of:

Frequency: f=1000Hz

Peak current: I=10~mAmp=0.01 Amp

Pulse width: seconds

So, how many electrons we have in each second?

By Q=It, we have

                           [math] N \times e=f \times I \times \Delta t [/math]

Where N is the total electron numbers hits target per second, e is electron charge and f, I and ∆t are given above. Number of particle per second is:

                           [math]  N = \frac {f \times I \times \Delta t}{e} [/math]

2.Calculating Energy deposited per second

If we find the energy deposited by each electron and multiply to the total number of electrons in each second, we will find the total energy per second deposited in radiator.

To find energy deposited by each electron, we need to use formula

                              [math] E_{dep~one}={(\frac{dE}{dx})}_{coll}\times t [/math]

Where is [math] E_{dep~one} [/math] is energy deposited by one electron, [math] {(\frac{dE}{dx})}_{coll} [/math] is mean energy loss (also stopping power) by collision of electron and [math] t [/math] is thickness of the radiator.

Actually, energy loss of a electron comes from two parts: 1) the emission of electromagnetic radiation arising from scattering in the electric field of a nucleus (bremsstrahlung); 2) Collisional energy loss when passing through matter. Bremsstrahlung will not contribute to the temperature, because it is radiation.

Stopping power can be found from nuclear data tables [math] (dE/dx)_{ave} [/math] and thickness is 0.001 times of radiation length. From Particle Data group we got radiation length and average total stopping powers around 15MeV for electrons in these materials from National Institute of Standards and Technology: Tungsten Stopping Power.

Table of Radiation Lengths

Note:These data is from Particle Data group,Link: [1].

Elements	Radiation Lengths [math] (g/cm^{2} )[/math]
W	6.76

Table of energy calculations

For the thickness of 0.001 Radiation Length (0.0001RL) of radiators. Note: [math](dE/dx)_{coll}[/math] is from National Institute of Standards and Technology. Link: [[2]])

Elements		t~( [math] g~cm^{-2}[/math])	[math]E_{(dep~one)}[/math] (MeV)	[math]E_{dep/s}[/math] (MeV/s)	[math]E_{dep/s}[/math] (J/s)
W	1.247	0.00676	0.00842972	[math]2.63*10^{10}[/math]	[math]4.21*10^{-3}[/math]

In above table,we took the total numbers of electrons per second and multiply it to Energy deposited by one electron,get total energy deposited per second (which is power).

                                  [math]P_{dep}= E_{dep}/s = ( E_{(dep~by~one)})\times(Number~of~electrons~per~second)[/math]

3.Calculating equilibrium temperature using Stefan–Boltzmann law

If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter. According to Stefan–Boltzmann law, this total power radiated will be

                                                        [math] P_{rad}[/math]= 2Aσ[math]T^{4}[/math]

Where T is radiating temperature P is the radiating power, A is surface area that beam incident and σ is Stefan–Boltzmann constant or Stefan's constant. To reach equilibrium temperature, Power deposited in and power radiated should be. So

                                                       [math] P_{dep}=P_{rad} [/math]

so

                                              T =[[math]  P_{dep}[/math]/(2Aσ)]^{1/4}

Table of equilibrium temperatures

For 2mm diameter spot size and 0.001 time Radiation Length thickness

Elements	d (m)	2A( [math] m^{2}[/math])	Stefan-Boltzmann Constant	[math]T_{equ}[/math] (K)
W	0.002	0.00000628	[math]5.6704*10^{-8}[/math]	329.8

4. Results for different Thicknesses and Spot sizes

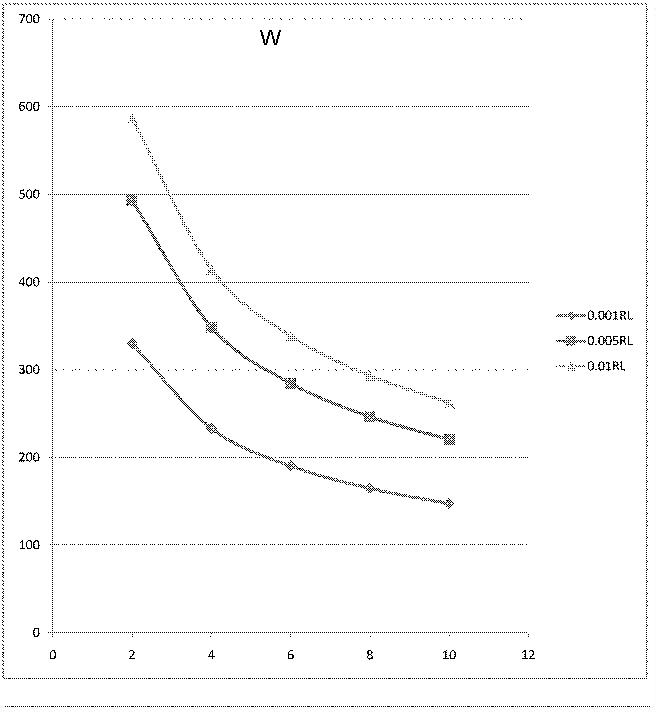
We can calculate separately for Al, W and Ti for different thickness and different beam spot diameter. Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.001, 0.005 and 0.01 times of Radiation Length, in beam spot of diameter of 2, 4, 6, 8, 10 mm.

W

Equilibrium temperature for W, unit is K. (Melting point of W is 3695K)

	2(mm)	4(mm)	6(mm)	8(mm)	10(mm)
0.001Rl	239.8 K	233.2 K	190.4 K	164.9 K	147.5 K
0.005Rl	493.2 K	348.7 K	248.7 K	246.6 K	220.6 K
0.01Rl	586.5 K	414.7 K	338.6 K	293.3 K	262.3 K

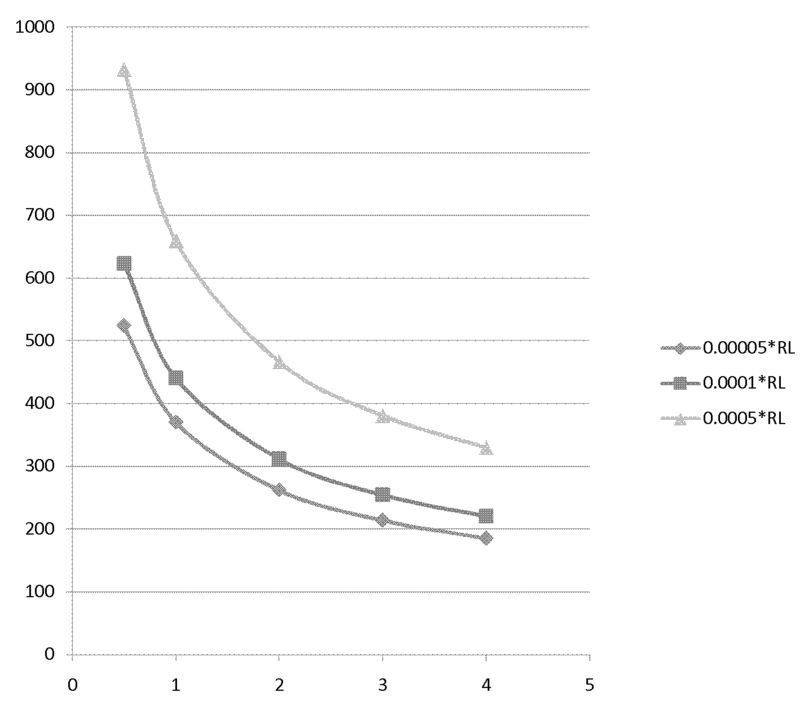
5. Results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width )

Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of 0.00001, 0.0005 and 0.0001 times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.

W

Equilibrium temperature for W, unit is K. (Melting point of Al is 3695K)

	1(mm)	2(mm)	3(mm)	4(mm)
0.00005Rl	370 K	262 K	214 K	158 K
0.0001Rl	441 K	312 K	254 K	220 K
0.0005Rl	660 K	446 K	381 K	330 K

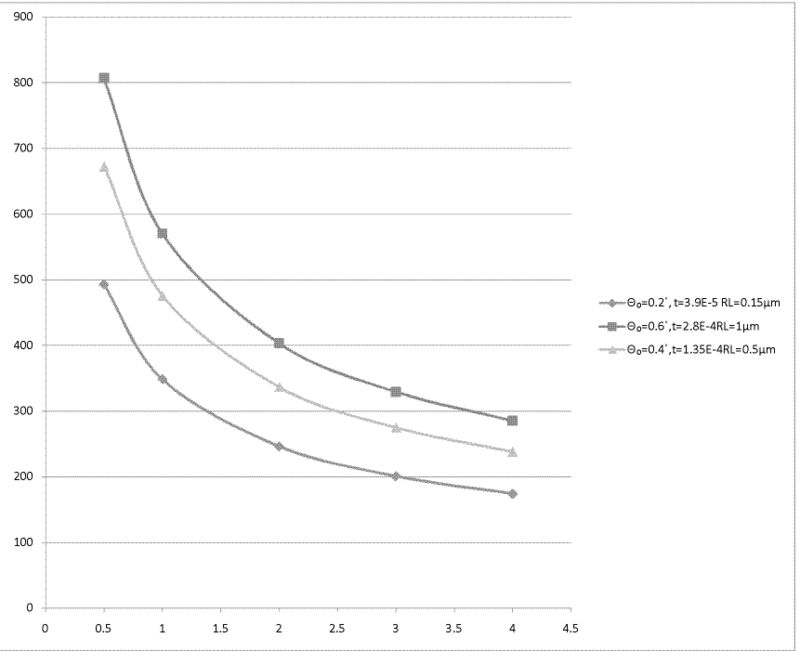
6. More results for worst cases ( 80mA peak current,1000Hz frequency, 50ns pulse width for Θ₀ = 0.2,0.4,0.6 dgrees)

Now we calculate temperature for Al, W, Ti and Fe for different thickness and different beam spot diameter in worst case . Following tables are temperature calculation for Al, W Ti and Fe in thickness of [math]3.9*10^{-5}[/math] (Θ₀ = [math]0.2^{o}[/math]), [math]1.35*10^{-4}[/math](Θ₀= [math]0.4^{o}[/math]) and [math]2.8*10^{-4}[/math](Θ₀ = [math]0.6^{o}[/math]) times of Radiation Length, in beam spot of diameter of 2, 3, 4 mm.

W