Counts Rate (44 MeV LINAC)

Go Back

Counts Rate for U238 (12.5 µm Ti converter)

LINAC parameters used in calculations

1) pulse width 50 ps
2) pulse current 50 A
3) repetition rate 300 Hz
4) energy 44 MeV

Number of electrons/sec on radiator

[math] 50\ \frac{Coulomb}{sec} \times \frac{1\cdot e^-}{1.6\cdot 10^{-19}C} \times 50ps \times 300Hz = 0.47 \cdot 10^{13} \frac{e^-}{sec}[/math]

Number of photons/sec on target

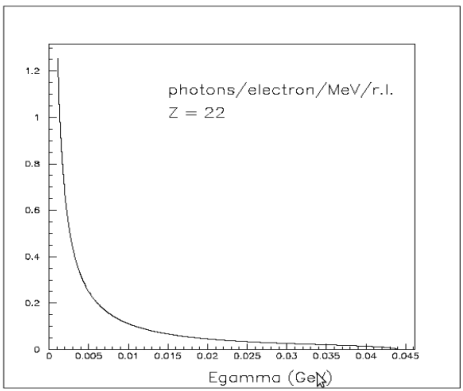
bremsstrahlung

in (10,20) MeV region we have about

    0.1 photons/electrons/MeV/r.l

radiation length

r.l.(Ti) = 3.59 cm
  
radiator thickness = 12.5 [math]\mu m[/math]

[math]\frac{12.5\ \mu m}{3.59\ cm} = 3.48 \cdot 10^{-4} \ r.l.[/math]

steps together...

[math]0.1\ \frac{\gamma 's}{(e^- \cdot MeV \cdot r.l.)} \times 3.48 \cdot 10^{-4} r.l. \times 10\ MeV \times 0.47 \cdot 10^{13} \frac{e^-}{sec}=1.64 \cdot 10^{9} \frac{\gamma}{sec}[/math]

Alex factor (GEANT4 calculation)

Collimation factor is

    6.85 % of total # of photons

then, incident flux on target is

[math]1.64 \cdot 10^{9} \frac{\gamma}{sec} \cdot 6.85\ % = 11.2 \cdot 10^{7} \frac{\gamma}{sec}[/math]

Number of neutrons/sec

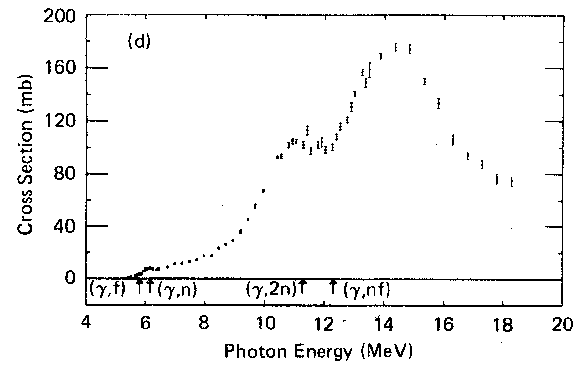
photonuclear cross section for [math]^{238}U(\gamma , n)[/math] reaction

J. T. Caldwell et all., Phys. Rev. C21, 1215 (1980):

in (10,20) MeV region the average cross section, say, is:

    130 mb

target thickness, [math]^{238}U[/math]

[math]\frac{19.1\ g/cm^3}{238.02\ g/mol} = 0.08\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ atoms}{mol} = 0.48\cdot 10^{23}\ \frac{atoms}{cm^3}[/math]

Let's target thickness = 1 mm:

[math]0.48\cdot 10^{23}\ \frac{atoms}{cm^3} \times 0.1\ cm = 0.48\cdot 10^{22}\ \frac{atoms}{cm^2}[/math]

neutrons per fission

   2.4 neutrons/fission

steps together...yeild

[math] Y = \frac{\gamma}{sec} \times t \times \sigma \times 2.4 = [/math]

[math] = 11.2 \cdot 10^{7} \frac{\gamma}{sec} \times 130\ mb \times 0.48\cdot 10^{22}\ \frac{atoms}{cm^2} \times 2.4 = 1.68 \cdot 10^{5}\   \frac{neutrons}{sec}[/math]

Worst Case Isotropic Neutrons

checking detector distance

we want:

     the time of flight of neutron >> the pulse width

take the worst case 10 MeV neutron:

[math] E_{tot} = E_{kin} + E_{rest} =  10\ MeV + 938\ MeV = 948\ MeV [/math]

[math] \gamma = \frac{E_{tot}}{m_p} = \frac{948\ MeV}{938\ MeV} = 1.0107 [/math]

[math] \gamma^2 = \frac{1}{1 - \beta^2} \ \ \  \rightarrow \ \ \ \beta = 0.145\ c[/math]

take the neutron detector 1 meter away:

[math] t = \frac{1\ m}{0.145\ c} = \frac{1\ m}{0.145\cdot 3\cdot 10^8\ m/sec} = 23\ ns [/math]

     23 ns >> 50 ps  <= time resolution is good

geometrical factor

taking real detector 3" x 2" => S is about 40 cm^2

1 meter away

fractional solid angle = [math]\frac{40\ cm^{2}}{4 \pi\ (100\ cm)^{2}} = 3.2 \cdot 10^{-4}[/math] <= geometrical acceptance

Yield

the yield per second:

[math]1.68 \cdot 10^{5}\ \frac{neutrons}{sec} \times 3.2 \cdot 10^{-4} = 53.8\ \frac{neutrons}{sec} [/math]

the yield per pulse:

[math] 53.8\ \frac{neutrons}{sec} \times \frac{1\ sec}{300\ pulses} = 0.18\ \frac{neutrons}{pulse} [/math] 

 53.8 neutrons/sec  <= this experiment is do able

 0.18 neutrons/pulse <= good for stopping pulse

Counts Rate for U238 (25 µm Al converter)

radiation length

r.l.(Al) = 8.89 cm
  
radiator thickness = 25 [math]\mu m[/math]

[math]\frac{25\ \mu m}{8.89\ cm} = 2.81 \cdot 10^{-4} \ r.l.[/math]

Calibration factor

The only difference from calculations above is:

1) radiation length:

    3.48 (for 12.5 µm Ti) / 2.81 (for 50 µm Al) = 1.24

Yield

 53.8 neutrons/sec * 1.24 = 66.7 neutrons/sec

 0.18 neutrons/pulse * 1.24 = 0.22 neutrons/pulse

Counts Rate for Deuteron (12.5 µm Ti converter)

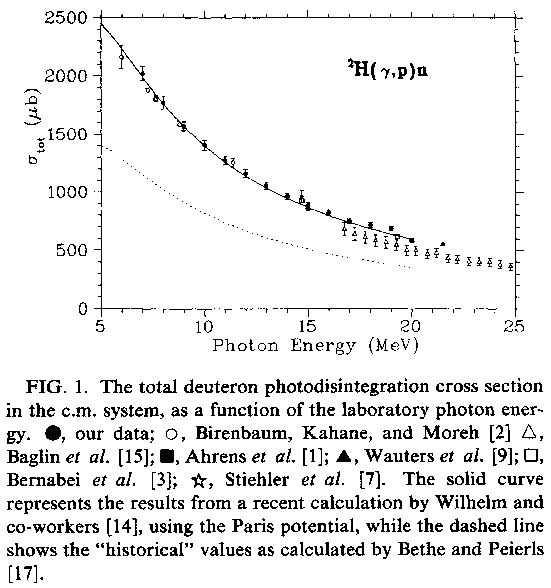
photonuclear cross section for [math] ^2H(\gamma , n) [/math] reaction

A. De Graeva et all., Phys. Rev. C45, 860 (1992):

in (10,20) MeV region the average cross section, say, is:

    1000 μb

target thickness, [math] D_2O [/math]

take [math]D_2O[/math], liquid (20°C):

[math] \frac{1.1056\ g/mL}{20.04\ g/mol} = 0.055\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ molecules}{mol} = 0.33\cdot 10^{23}\ \frac{molecules}{cm^3} [/math]

[math] 0.33\cdot 10^{23}\ \frac{molecules}{cm^3} \times \frac{2\ deuterons}{molecule} = 0.66\cdot 10^{23}\ \frac{deuterons}{cm^3} [/math]

Let's target thickness = 10 cm:

[math]0.66\cdot 10^{23}\ \frac{atoms}{cm^3} \times 10\ cm = 66\cdot 10^{22}\ \frac{atoms}{cm^2}[/math]

angular distribution of neutron

1) from relativistic kinematic:

7	64313	8.28E+09	1.29E+05
15	16689	2.06E+09	1.23E+05
24	18448	2.12E+09	1.15E+05
29	22447	No Data	No Data
33	22638	3.40E+09	1.50E+05
61	19981	3.14E+09	1.57E+05
73	18898	3.09E+09	1.63E+05
77	18668	3.03E+09	1.62E+05
101	390278	2.02E+09	5.17E+03
105	406062	2.19E+09	5.39E+03
138	13643	4.07E+09	2.98E+05
142	14847	3.47E+09	2.34E+05
154	30990	4.38E+09	1.41E+05
158	50581	1.71E+09	3.38E+04

Calibration factor

The only difference from calculations above is:

1) cross section:

    1000 μb (D) / 130 mb (238U) = 1/130

2) target thickness:

   [math] \frac{66\cdot 10^{22}\ atoms/cm^2\ (D)}{0.48\cdot 10^{23}\ atoms/cm^2\ (^{238}U)} = 66/0.48 [/math]

3) neutrons per reaction:

   1 neutron (D) / 2.4 neutrons(238U) = 1/2.4

4) geometrical factor:

   assume for now is 1

total calibration factor is:

  [math]\frac{1}{130} \times \frac{66}{0.48} \times \frac{1}{2.4} \times 1= 0.441[/math]

Yield

saying all other factors is the same =>

the yield per second :

[math] 53.8\ \frac{neutrons}{sec} \times 0.441 = 23.7\ \frac{neutrons}{sec} [/math]

the yield per pulse:

[math] 23.7\ \frac{neutrons}{sec} \times \frac{1\ sec}{300\ pulses} = 0.079\ \frac{neutrons}{pulse} [/math]

Go Back