Difference between revisions of "Counts Rate (44 MeV LINAC)"
Jump to navigation
Jump to search
| Line 32: | Line 32: | ||
<math>12.5\mu m/3.59 cm = 3.48 \cdot 10^{-4} \ r.l.</math><br> | <math>12.5\mu m/3.59 cm = 3.48 \cdot 10^{-4} \ r.l.</math><br> | ||
| − | ==steps together...== | + | ===steps together...=== |
<math>0.1\ \frac{\gamma 's}{(e^- \cdot MeV \cdot r.l.)} \times 3.48 \cdot 10^{-4} r.l. \times 10\ MeV \times 0.47 \cdot 10^{13} \frac{e^-}{sec}=1.64 \cdot 10^{9} \frac{\gamma}{sec}</math><br><br> | <math>0.1\ \frac{\gamma 's}{(e^- \cdot MeV \cdot r.l.)} \times 3.48 \cdot 10^{-4} r.l. \times 10\ MeV \times 0.47 \cdot 10^{13} \frac{e^-}{sec}=1.64 \cdot 10^{9} \frac{\gamma}{sec}</math><br><br> | ||
| Line 47: | Line 47: | ||
| − | =Number of neutrons/sec (yields)= | + | ==Number of neutrons/sec (yields)== |
| − | ==photonuclear cross section <math>\sigma (\gamma , F)</math> for <math>^{238}U</math>== | + | ===photonuclear cross section <math>\sigma (\gamma , F)</math> for <math>^{238}U</math>=== |
[[File:phofission_sigma_U238.png]] | [[File:phofission_sigma_U238.png]] | ||
| Line 57: | Line 57: | ||
'''130 mb''' | '''130 mb''' | ||
| − | ==target thickness, <math>^{238}U</math>== | + | ===target thickness, <math>^{238}U</math>=== |
<math>\frac{19.1\ g/cm^3}{238.02\ g/mol} = 0.08\ \frac{mol}{cm^3} = 0.08\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ atoms}{mol} = 0.48\cdot 10^{23}\ \frac{atoms}{cm^3}</math> | <math>\frac{19.1\ g/cm^3}{238.02\ g/mol} = 0.08\ \frac{mol}{cm^3} = 0.08\ \frac{mol}{cm^3} \times \frac{6.02\cdot 10^{23}\ atoms}{mol} = 0.48\cdot 10^{23}\ \frac{atoms}{cm^3}</math> | ||
| Line 65: | Line 65: | ||
<math>0.48\cdot 10^{23}\ \frac{atoms}{cm^3} \times 1\ cm = 0.48\cdot 10^{23}\ \frac{atoms}{cm^2}</math> | <math>0.48\cdot 10^{23}\ \frac{atoms}{cm^3} \times 1\ cm = 0.48\cdot 10^{23}\ \frac{atoms}{cm^2}</math> | ||
| − | ==neutrons per fission== | + | ===neutrons per fission=== |
'''2.4 neutrons/fission''' | '''2.4 neutrons/fission''' | ||
| − | ==steps together...yeild== | + | ===steps together...yeild=== |
<math> Y = \frac{\gamma}{sec} \times t \times \sigma \times 2.4 = </math><br> | <math> Y = \frac{\gamma}{sec} \times t \times \sigma \times 2.4 = </math><br> | ||
| Line 75: | Line 75: | ||
<math> = 8.2 \cdot 10^{7} \frac{\gamma}{sec} \times 130\ mb \times 0.48\cdot 10^{23}\ \frac{atoms}{cm^2} \times 2.4 = 1.2 \cdot 10^{6}\ \frac{neutrons}{sec}</math><br><br> | <math> = 8.2 \cdot 10^{7} \frac{\gamma}{sec} \times 130\ mb \times 0.48\cdot 10^{23}\ \frac{atoms}{cm^2} \times 2.4 = 1.2 \cdot 10^{6}\ \frac{neutrons}{sec}</math><br><br> | ||
| − | =Worst Case Isotropic Neutrons= | + | ==Worst Case Isotropic Neutrons== |
Let's say we have: | Let's say we have: | ||
| Line 87: | Line 87: | ||
finally we have | finally we have | ||
| − | <math>1.2 \cdot 10^{6}\ \frac{neutrons}{sec} \times \frac{1}{4} \cdot 10^{-4} = | + | <math>1.2 \cdot 10^{6}\ \frac{neutrons}{sec} \times \frac{1}{4} \cdot 10^{-4} = 30\ \frac{neutrons}{sec} </math><br> |
| − | '''Therefore, this experiment is really doable.''' | + | '''Therefore, this experiment is really doable.'''<br><br> |
| + | |||
| + | |||
| + | =Counts Rate for Deuteron= | ||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
Revision as of 16:34, 19 May 2010
Counts Rate for U238
LINAC parameters used in calculations
1) pulse width 50 ns
2) pulse current 50 A
3) repetition rate 300 Hz
4) energy 44 MeV
Number of electrons/sec on radiator
Number of photons/sec from radiator
bremsstrahlung
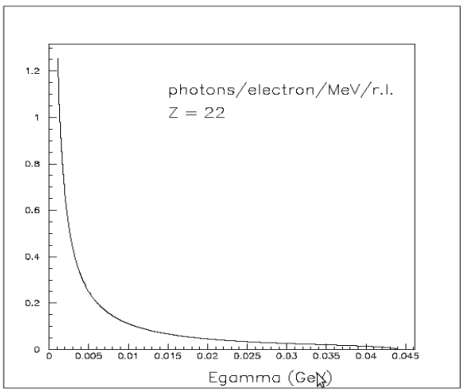
in (10,20) MeV region we have about
0.1 photons/electrons/MeV/r.l
radiation length
r.l.(Ti) = 3.59 cm
radiator thickness = 12.5
steps together...
Collimation factor
Collimation factor is
4-6 % of total # of photons (Alex, GEANT calculation)
then, incident flux on target is
Number of neutrons/sec (yields)
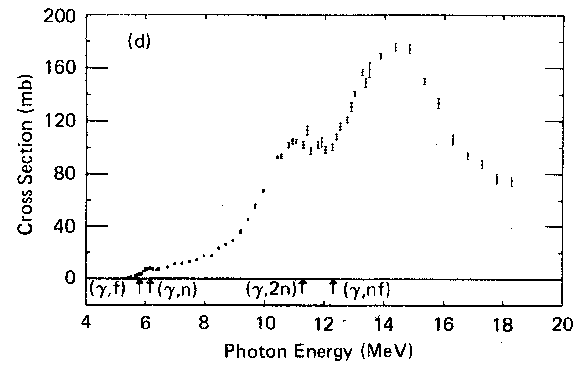
photonuclear cross section for
in (10,20) MeV region the average cross section is:
130 mb
target thickness,
Target thickness = 1 cm:
neutrons per fission
2.4 neutrons/fission
steps together...yeild
Worst Case Isotropic Neutrons
Let's say we have:
radius detector = 1 cm
1 meter away
fractional solid angle = <= geometrical acceptance
finally we have
Therefore, this experiment is really doable.