Geometry (44 MeV LINAC exit port)

Go Back

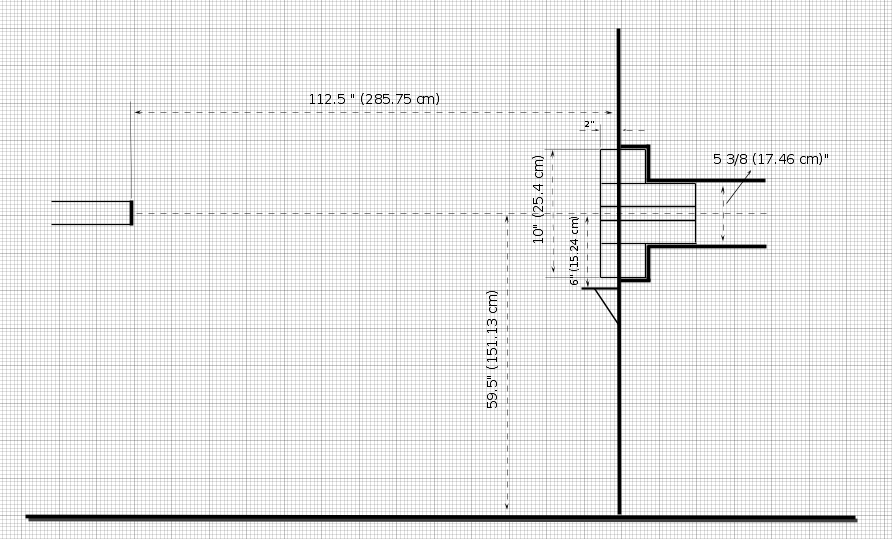
Some measurements of 90 experimental degree exit port

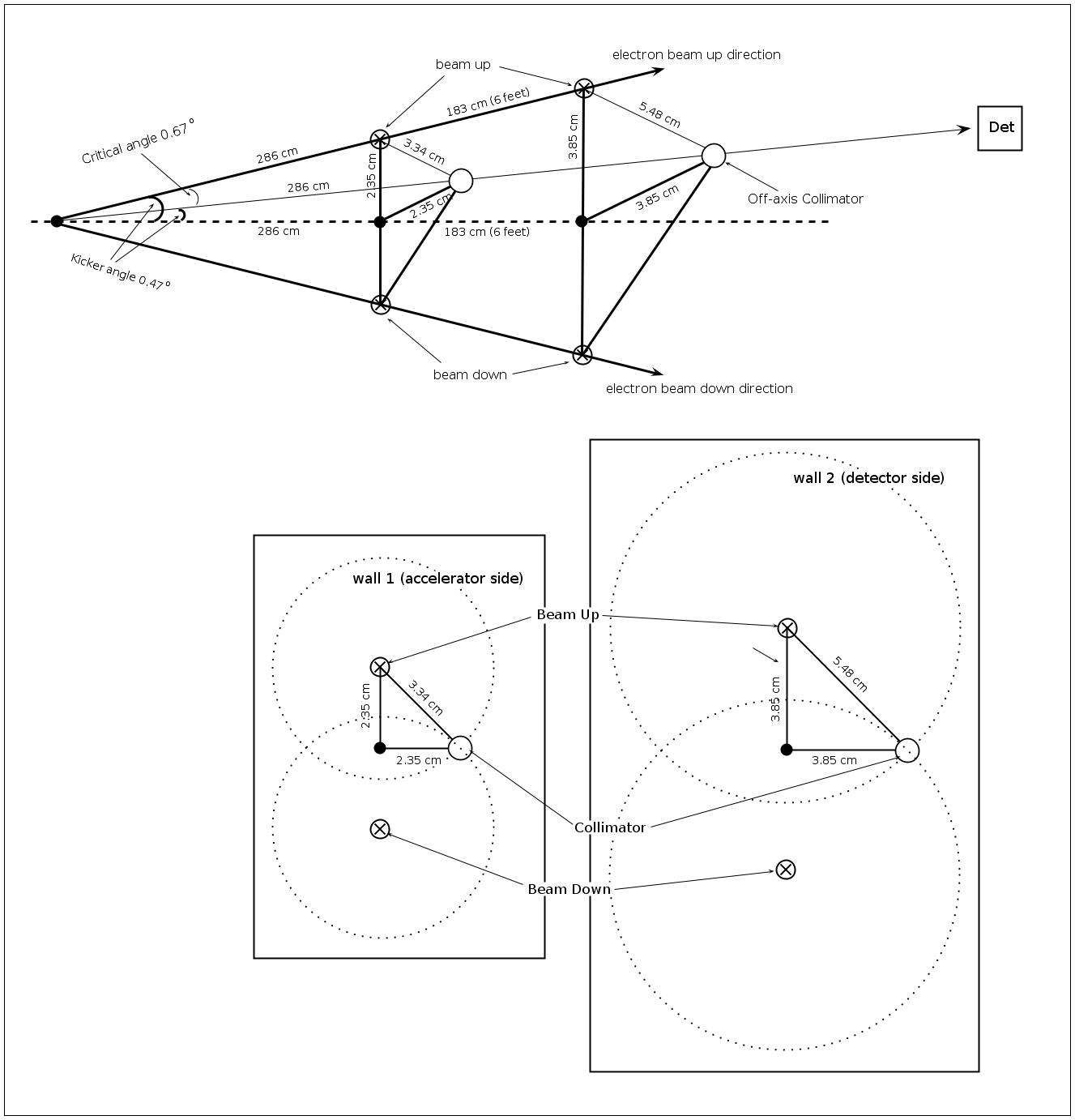
Critical angle and displacement calculations

[math]\Theta = \frac{m_ec^2}{E_{beam}} = \frac{0.511\ MeV}{44\ MeV} = 0.67\ ^o[/math]

Kicker angle and displacement calculations

accelerator's side wall

  [math]\Delta = 286\ cm\ *\ \tan(0.67^o) = 3.34\ cm[/math] 

  [math]x^2+x^2 = 3.34^2\ cm \ \ \Rightarrow\ \  x = 2.36\ cm[/math]

  [math]\Delta = 2.36\ cm \ \ \Rightarrow\ \ \tan^{-1}\left(\frac{2.36}{286}\right) = 0.47\ ^o[/math]

detector's side wall

  [math]\Delta = (286\ cm + 183\ cm)\ *\ \tan(0.67^o) = 5.48\ cm[/math]

  [math]\Delta = (286\ cm + 183\ cm)\ *\ \tan(0.47^o) = 3.85\ cm[/math]

Off-axis collimation geometry

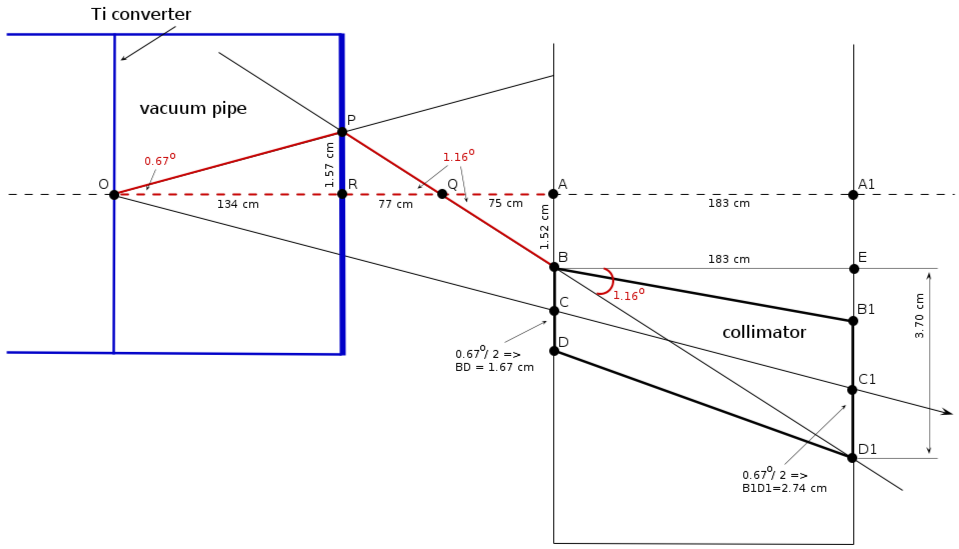
Vacuum pipe location ([math] \Theta_c/2[/math])

collimator location

1) center position:

  [math]286\ cm \cdot \tan (0.47) = 2.35\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.47) = 3.85\ cm[/math]  (wall 2)

2) collimator diameter:

  [math]\Theta_c/2 = 0.67^o/2 = 0.335^o[/math]

  [math]286\ cm \cdot \tan (0.335) = 1.67\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.335) = 2.74\ cm[/math]  (wall 2)

collimator critical angle

  [math] AB = AC - BD/2 = (2.35 - 1.67/2)\ cm = 1.52\ cm [/math]

  [math] A_1D_1 = A_1C_1 + B_1D_1/2 = (3.85 + 2.74/2)\ cm = 5.22\ cm [/math]

  [math] ED_1 = A_1D_1 - A_1E = (5.22 - 1.52)\ cm = 3.70\ cm [/math]
 

from triangle [math]BED_1[/math]:

  [math] \tan (\alpha) = \frac{3.70\ cm}{183\ cm} \Rightarrow \alpha = 1.16^o[/math]

minimal distance from the wall

from triangle FAB:

  [math] FA = \frac{AB}{\tan (1.16^o)} = \frac{1.52\ cm}{\tan (1.16^o)} = 75\ cm [/math]

collimator and pipe geometry

Vacuum pipe location ([math] \Theta_c/4[/math])

collimator location

1) center position:

  [math]286\ cm \cdot \tan (0.47) = 2.35\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.47) = 3.85\ cm[/math]  (wall 2)

2) collimator diameter:

  [math]\Theta_c/4 = 0.67^o/4 = 0.168^o[/math]

  [math]286\ cm \cdot \tan (0.168) = 0.84\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.168) = 1.38\ cm[/math]  (wall 2)

collimator critical angle

  [math] AB = AC - BD/2 = (2.35 - 0.84/2)\ cm = 1.93\ cm [/math]

  [math] A_1D_1 = A_1C_1 + B_1D_1/2 = (3.85 + 1.38/2)\ cm = 4.54\ cm [/math]

  [math] ED_1 = A_1D_1 - AB = (4.54 - 1.93)\ cm = 2.61\ cm [/math]
 

from triangle [math]BED_1[/math]:

  [math] \tan (\alpha) = \frac{2.61\ cm}{183\ cm} \Rightarrow \alpha = 0.82^o[/math]

minimal distance from the wall

from triangle FAB:

  [math] FA = \frac{AB}{\tan (0.82^o)} = \frac{1.93\ cm}{\tan (0.82^o)} = 135\ cm [/math]

collimator and pipe geometry

Go Back