Geometry (44 MeV LINAC exit port)

Go Back

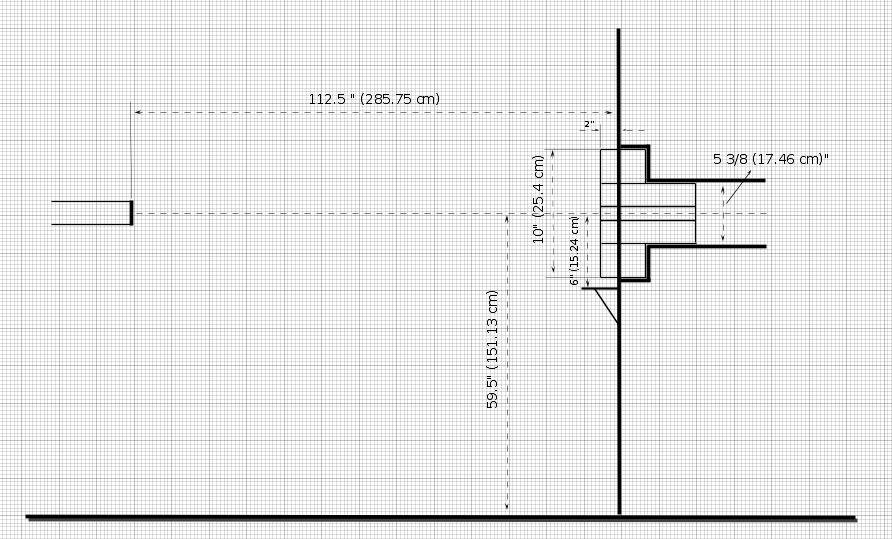
Some measurements of 90 experimental degree exit port

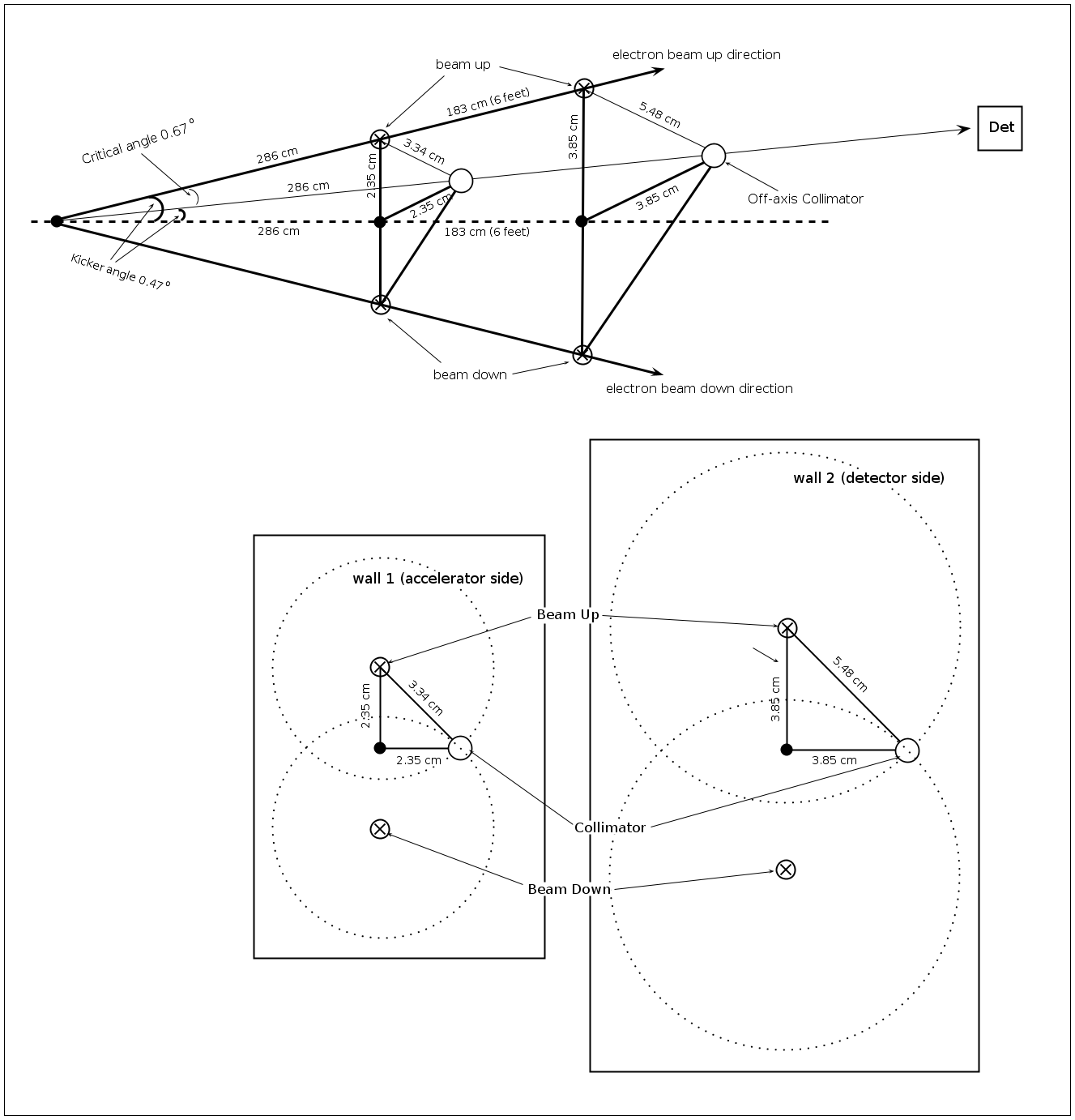
Critical angle and displacement calculations

[math]\Theta = \frac{m_ec^2}{E_{beam}} = \frac{0.511\ MeV}{44\ MeV} = 0.67\ ^o[/math]

Kicker angle and displacement calculations

accelerator's side wall

  [math]\Delta = 286\ cm\ *\ \tan(0.67^o) = 3.34\ cm[/math] 

  [math]x^2+x^2 = 3.34^2\ cm \ \ \Rightarrow\ \  x = 2.36\ cm[/math]

  [math]\Delta = 2.36\ cm \ \ \Rightarrow\ \ \tan^{-1}\left(\frac{2.36}{286}\right) = 0.47\ ^o[/math]

detector's side wall

  [math]\Delta = (286\ cm + 183\ cm)\ *\ \tan(0.67^o) = 5.48\ cm[/math]

  [math]\Delta = (286\ cm + 183\ cm)\ *\ \tan(0.47^o) = 3.85\ cm[/math]

Off-axis collimation geometry

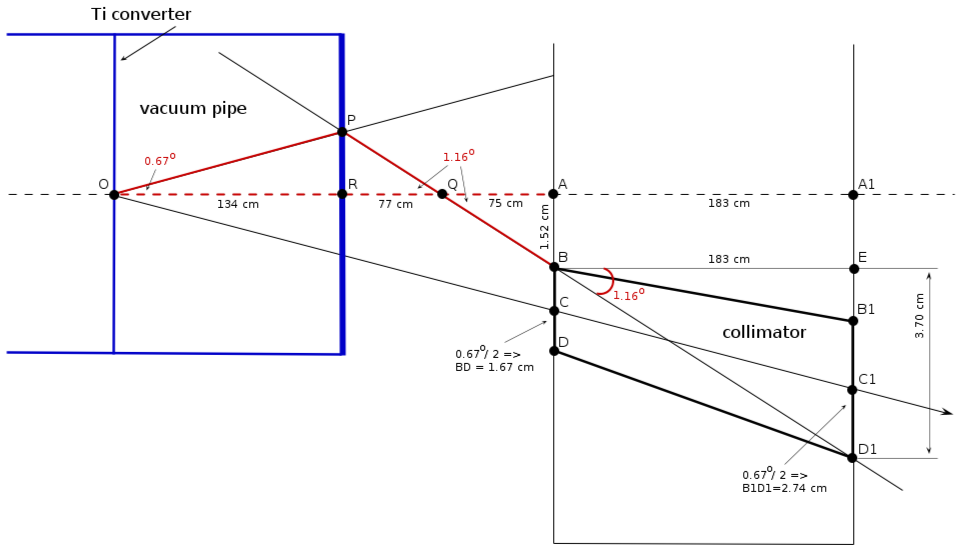
Vacuum pipe location (only the kicker angle)

collimator location

1) center position

  [math]286\ cm \cdot \tan (0.47) = 2.35\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.47) = 3.85\ cm[/math]  (wall 2)

2) assume diameter is [math]\Theta_c/2 = 0.67^o/2 = 0.335^o[/math]

  [math]286\ cm \cdot \tan (0.335) = 1.67\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.335) = 2.74\ cm[/math]  (wall 2)

collimator critical angle

  AB = AC - BD/2 = (2.35 - 1.67/2) cm = 1.52 cm

  A1D1 = A1C1 + B1D1/2 = (3.85 + 2.74/2) cm = 5.22 cm

  ED1 = A1D1 - AB = (5.22 - 1.52) cm = 3.70 cm
 

from triangle [math]BEB_1[/math]:

  [math] \tan (\alpha) = \frac{3.70\ cm}{183\ cm} \Rightarrow \alpha = 1.16^o[/math]

minimal distance from the wall

1) from triangle QAB:

  [math] QA = \frac{AB}{\tan (1.16^o)} = \frac{1.52\ cm}{\tan (1.16^o)} = 75\ cm [/math]

3) from triangles OPR and QPR:

  OQ = OA - QA = (286 - 75) cm = 211 cm

  [math] RQ\cdot \tan (1.16^o) = (211 - RQ)\cdot \tan (0.47^o) \Rightarrow[/math]

  [math] RQ = 211\cdot \frac{tan (0.47^o)}{tan (0.47^o) + tan (1.16^o)} = 61\ cm[/math]

4) minimal distance:

  RA = RQ + QA = (61 + 75) cm = 136 cm (from the wall)

  OR = OA + RA = (286 + 136) cm = 150 cm (from the wall)

collimator and pipe geometry

Vacuum pipe location (kicker angle + multiple scattering angle)

1) take multiple scattering angle [math] \Tetha = 0.27^o[/math]

  [math] 0.47^o \longrightarrow (0.47^o - 0.27^o) = 0.20^o[/math]

  [math] RQ = 211\cdot \frac{tan (0.20^o)}{tan (0.20^o) + tan (1.16^o)} = 31\ cm[/math]

4) minimal distance:

  RA = RQ + QA = (31 + 75) cm = 106 cm (from the wall)

  OR = OA + RA = (286 + 106) cm = 180 cm (from the wall)

Go Back