Geometry (44 MeV LINAC exit port)

Go Back

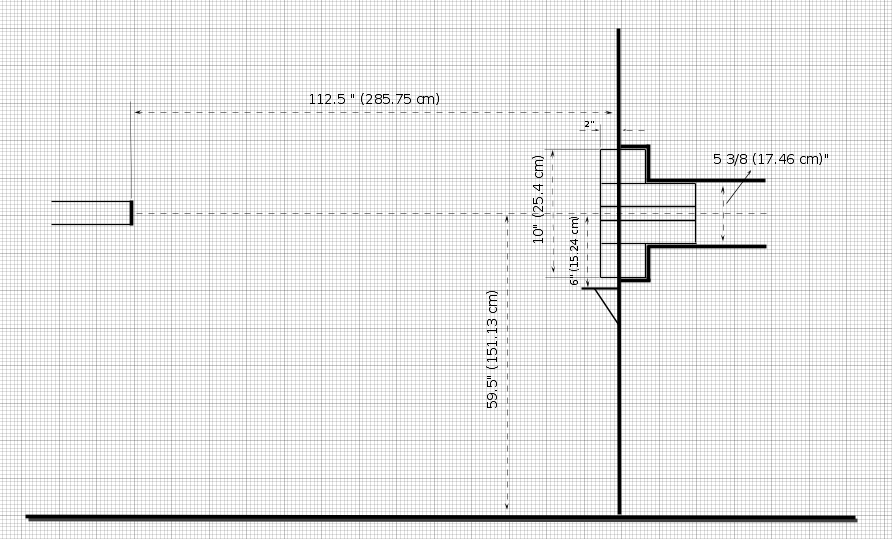
Some measurements of 90 experimental degree exit port

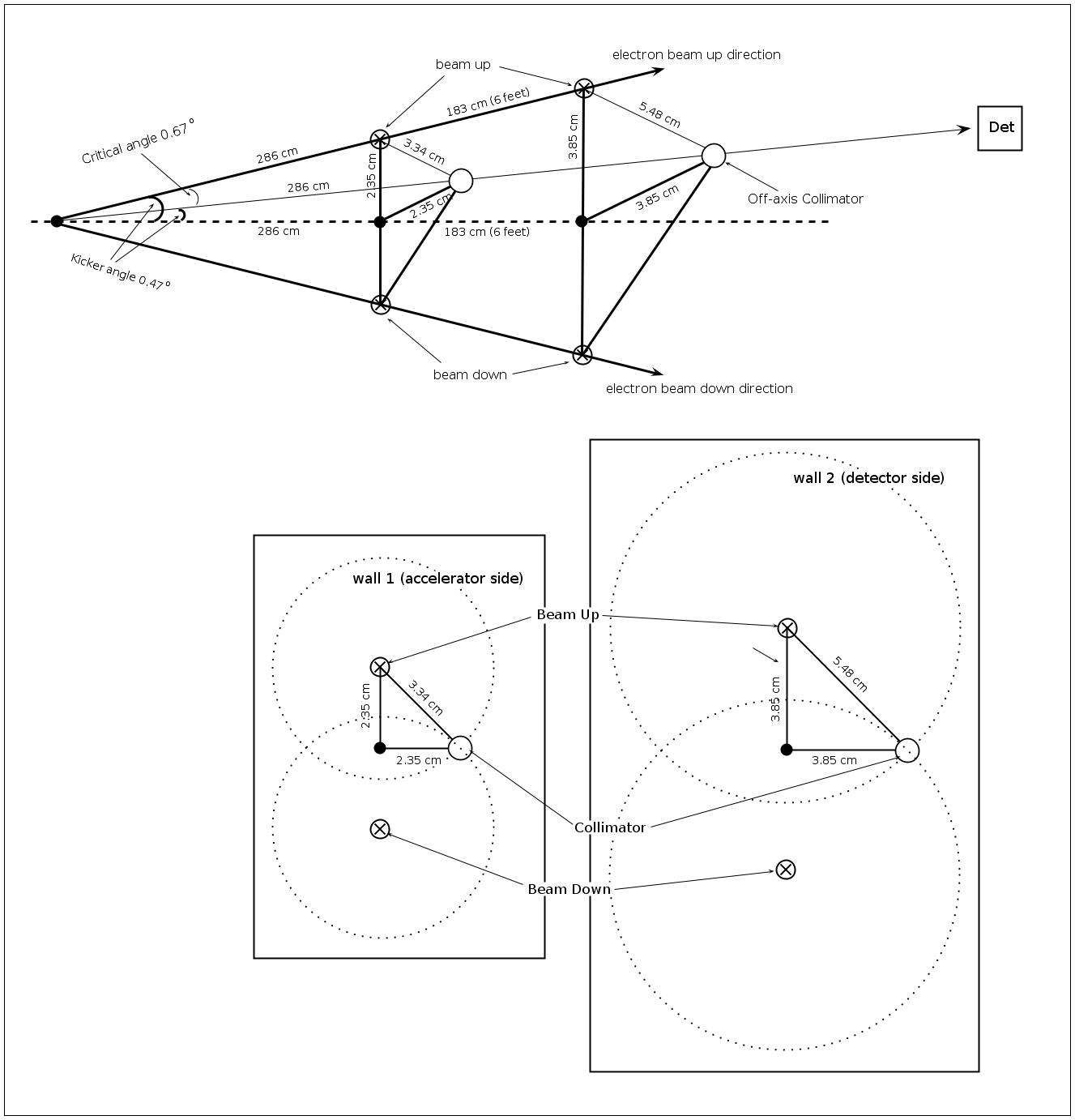
Critical angle and displacement calculations

[math]\Theta = \frac{m_ec^2}{E_{beam}} = \frac{0.511\ MeV}{44\ MeV} = 0.67\ ^o[/math]

Kicker angle and displacement calculations

accelerator's side wall

  [math]\Delta = 286\ cm\ *\ \tan(0.67^o) = 3.34\ cm[/math] 

  [math]x^2+x^2 = 3.34^2\ cm \ \ \Rightarrow\ \  x = 2.36\ cm[/math]

  [math]\Delta = 2.36\ cm \ \ \Rightarrow\ \ \tan^{-1}\left(\frac{2.36}{286}\right) = 0.47\ ^o[/math]

detector's side wall

  [math]\Delta = (286\ cm + 183\ cm)\ *\ \tan(0.67^o) = 5.48\ cm[/math]

  [math]\Delta = (286\ cm + 183\ cm)\ *\ \tan(0.47^o) = 3.85\ cm[/math]

Off-axis collimation geometry

Vacuum pipe

Collimator location

1) center position

  [math]286\ cm \cdot \tan (0.47) = 2.35\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.47) = 3.85\ cm[/math]  (wall 2)

2) assume diameter is [math]\Theta_c/2 = 0.67^o/2 = 0.335^o[/math]

  [math]286\ cm \cdot \tan (0.335) = 1.67\ cm[/math]  (wall 1)

  [math](286 + 183)\ cm \cdot \tan (0.335) = 2.74\ cm[/math]  (wall 2)

Collimator critical angle

  AB = AC - BD/2 = (2.35 - 1.67/2) cm = 1.52 cm

  A1D1 = A1C1 + B1D1/2 = (3.85 + 2.74/2) cm = 5.22 cm

  ED1 = A1D1 - AB = (5.22 - 1.52) cm = 3.70 cm
 

from triangle [math]BEB_1\lt math\gt \lt math\gt \tan (\alpha) = \frac{3.70\ cm}{183\ cm} \Rightarrow \alpha = 1.16^o[/math]

Go Back