FC Analysis

Go Back

FC analysis using pulse by pulse ADC channel mean value distribution

For each beam pulse:

[math] ADC_{avg}^{pulse}=\frac{\sum_{i=1}^{16}{ADC_{i}*i}}{\sum_{i=1}^{16}{ADC_{i}}};[/math]

For distribution over all beam pulses:

[math] ADC_{ave}=\frac{\sum_{i=1}^{pulses}{ADC_{avg}^{pulse}}}{pulses};[/math]

[math] ADC_{sigma}={ \sqrt{\frac{1}{pulses}\sum_{i=1}^{pulses}{\left(ADC_{avg}^{pulse} - ADC_{avg}\right)^{2}}}};[/math]

Here is:
1. ADC# = bridge#
2. Pulse# = ReadOut# = Entry# = Event#

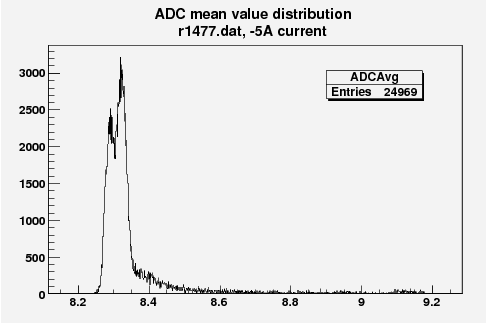
Some examples of ADC mean value distribution. Here are:
1. x axis: ADC mean value for one pulse
2. y axis: number of pulse w/ that ADC mean value

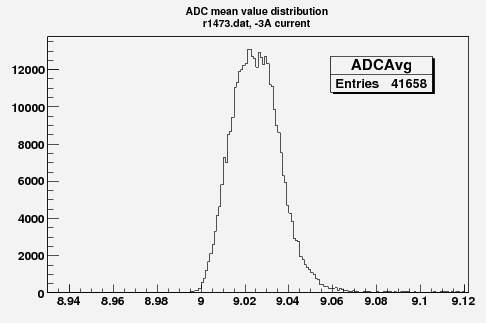
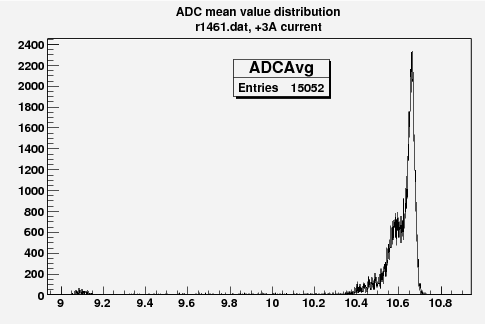
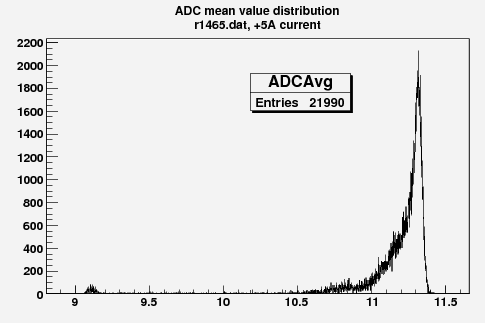
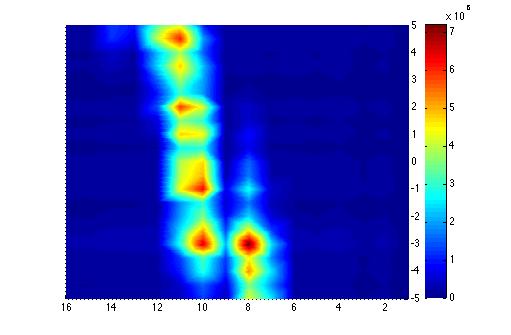
Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis).

Go Up