Simulating Particle Trajectories

This article discusses numerical simulations of particle trajectories in the "silver" permanent magnet.

Description of Problem

The general problem of modeling relativistic particle trajectories in electromagnetic fields boils down to solving the following system of six differential equations:

[math]\frac{d\vec{x}}{dt}=\vec{v}=\frac{1}{\gamma m_0}\vec{p}[/math]

[math]\frac{d\vec{p}}{dt}=q\left(\vec{E}+\frac{1}{\gamma m_0}\vec{p}\times\vec{B}\right)[/math]

where [math]\vec{x}[/math] is the position of the particle, [math]\vec{p}[/math] is the momentum of the particle, [math]m_0[/math] is the rest energy of the particle, and [math]\gamma[/math] is the usual relativistic factor. These equations are solved subject to an appropriate set of boundary conditions, usually the initial position and momentum of the particle.

In simple cases, such as when the fields are uniform, this set of equations can be solved analytically. However, for the "silver" permanent magnet we plan on using for the pair spectrometer, the fields are anything but uniform. In such a case, the system must be solved numerically.

Description of Code

The code, found here, solves the above system of equations using an embedded 8th order Runge-Kutta Prince-Dormand method with 9th order error estimates with adaptive stepsize control, as implemented in the GNU Scientific Library [1]. The zip file contains the relevant source and a script which should build the executable on any unix system with GSL installed in the usual place.

When executing the code, you must specify an input file on the command line. The input file is fairly simple. The first line of the input file is either a "0" or some integer greater than zero, and tells the program to run in "detailed output" or "scan" mode, respectively. In "detailed output" mode, the next five lines specify the energy of the initial gamma ray, the energy of the electron (the energy of the positron is assumed to be the difference of these two numbers), the angle between the axis of the magnet and the photon beam, the "Y" position of the conversion site above the magnet yoke, and the "X" position of the conversion site relative to the left edge of the magnet. In "scan" mode, the integer on the first line tells the program how many cases to run. Only two additional lines are needed: the energy of the photon and the "X" position of the conversion site. Examples of such input files are provided here (detailed mode) and here (scan mode).

The program output also depends on the program mode. In the "detailed output" mode, everything is written to stdout, and can be directed to a file using the ">" director. The output begins with a header, each line of which begins with the "#" character. The header lists the physical properties of the particle, the conditions read from the input file, and the corresponding initial positions and momenta of the electron and positron. Following the header, the program writes four columns of data: the time (in seconds) and the x, y, and z coordinates (in meters).

In "scan" mode, the program randomly selects an electron energy, angle of the magnet axis relative to the beam, and a conversion site "Y" coordinate, all subject to appropriate reasonable limits and kinematic constraints. It then models the trajectory of the particle until either the particle is sufficiently far from the detector, or a certain maximum time is reached. The program then evaluates the angles of the particles' final trajectories relative to the initial photon beam and assigns a flag as follows:

Flag codes for "scan" mode

0	Electron hits the yoke
1	Neither particle has an exit angle greater than 90 degrees
2	Only the electron has an exit angle greater than 90 degrees
3	Only the positron has an exit angle greater than 90 degrees
4	Both particles have exit angles greater than 90 degrees (ideal)
5	The electron gets trapped in the magnetic field
6	The positron gets trapped in the magnetic field

Ideally we want to tag both particles in coincidence with both particles exiting the beam at an angle greater than 90 degrees, hence the classifications in the table above.

Also, in "scan" mode, the program writes output to three places. The primary output is written to stdout, and can be directed to a file. This output consists of a header (each line of which begins with "#") listing the parameters passed to the program in the input file. The output itself is in five columns, consisting of the iteration number, the energy of the electron (in MeV), the angle of the magnet axis relative to the beam (in degrees), the height of the conversion site above the yoke (in meters), and the output flag as described above. Each line of output ends with a character "X" to facilitate extracting iterations that returned a particular flag using the grep command.

Progress output is written to stderr, and for each run that results in a flag greater than one an input file (for "detailed output" mode) is written.

The magnetic field, as implemented in the code

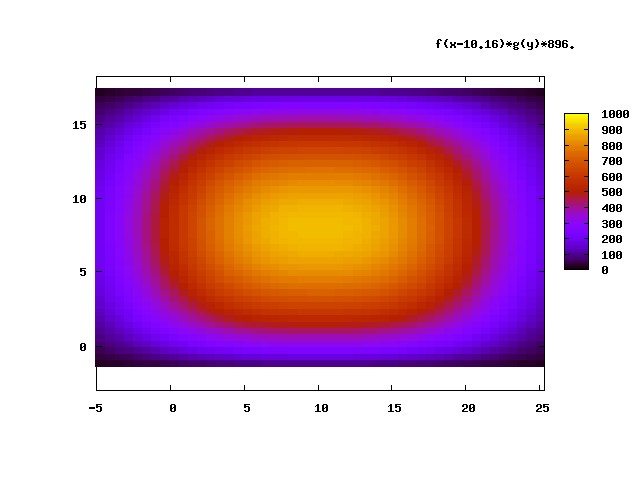
The measured magnetic field for the "silver" permanent magnet can be found here or here. To implement this field in the code, I performed a least squares fit to the data using a function of the form

[math]B\left(x,y\right)=-B_{max}f\left(x\right)g\left(y\right)[/math]

with

[math]f\left(x\right)=a_1\exp\left(-\frac{\left|\left|x+a_2\right|^{a_3}\right|}{2a_4^2}\right)[/math]

[math]g\left(y\right)=b_1y^2+b_2y+b_3[/math]

where [math]x[/math] and [math]y[/math] are in centimeters, [math]B_{max}[/math] is the maximum field (0.0896 Tesla), and the [math]a_i[/math] and [math]b_i[/math] are constants. These functional forms were chosen due to their good fit to the provided measured fields. The code explicitly puts a lower bound of zero on the magnetic field at any point in space. The [math]a_i[/math] constants turn out to be 1.0019, 0.064866, 2.74157, and 23.4233, and the [math]b_i[/math] constants are -0.0107702, 0.174007, and 0.305011. A map of this functional form for the field is shown below. The units for the field are in Gauss (they were converted to Tesla in the code), and the units for the x and y axes are centimeters. The lower left corner of the magnet is at (0,0).

Limitations of the Code

The code does not take into account any power radiated away as the charged particles accelerate. Such power loss is given by the Lienard formula,

[math] \frac{dE}{dt}=-\frac{\mu_0q^2\gamma^6}{6\pi c}\left(\vec{a}\cdot\vec{a}-\left|\frac{\vec{v}\times\vec{a}}{c}\right|^2\right)[/math]

For energies and speeds typical of what we expect to see in the pair spectrometer, these power losses are negligible. Future iterations of the code may include such power losses, but their value to the current problem when compared to the difficulty of implementing such losses does not justify the task for the time being.

Results of parameter space scans

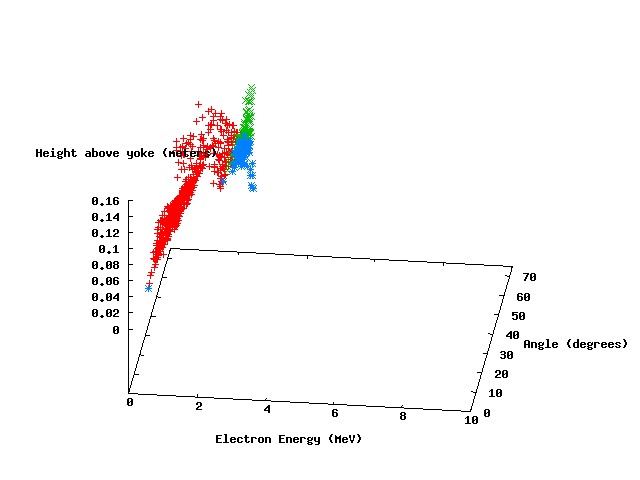
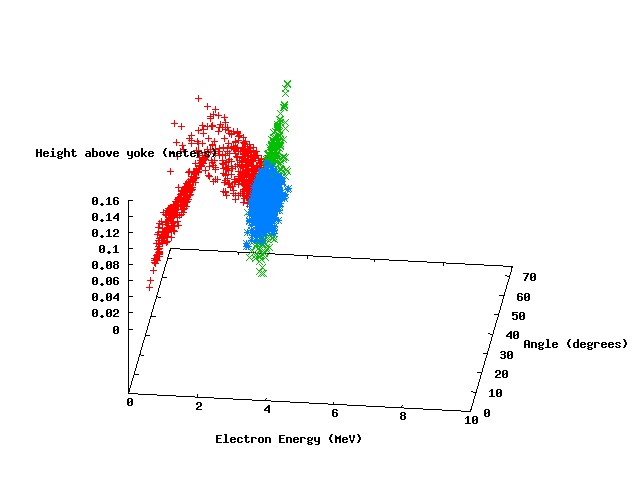
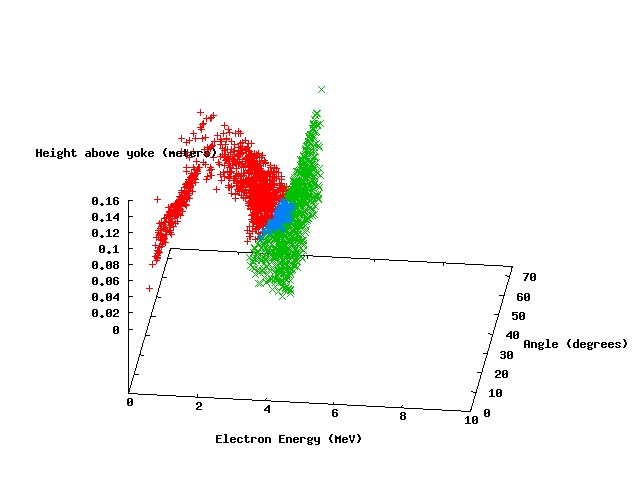
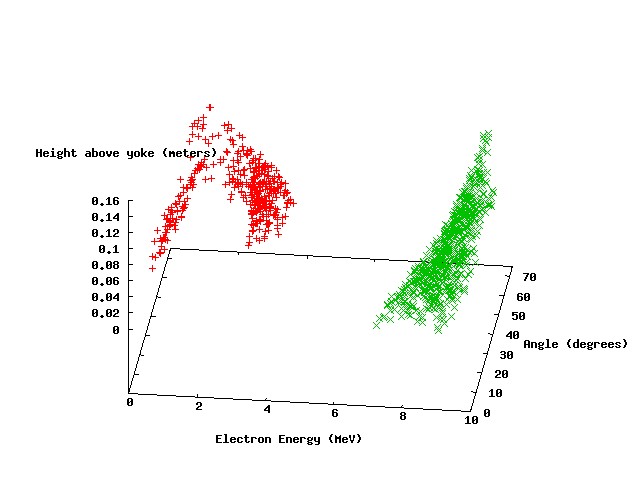
The following scatter plots show the results of four parameters scans, with photon energies of 3 MeV, 4 Mev, 5 MeV, and 10 MeV, respectively.

The points in red represent parameter sets where the electron leaves the magnetic field with an exit angle greater than 90 degrees. The green points represent a similar condition for the positron, and the blue points represent parameter sets where both particles leave with exit angles greater than 90 degrees (our "ideal" scenario). It can be seen that the ideal parameter space is larger for the lower energy photons (not surprisingly), but there is still a significant set of parameters at 5 MeV incident energy that meet the ideal criteria.

"Ideal" orientation of magnet for 5 MeV photons

The center of the ideal region of parameter space for 5 MeV photons has (approximately) the following characteristics:

• The electron energy is about 3.5 MeV (meaning the positron energy is about 1.5 MeV)
• The angle between the magnet axis and the original beam is about 50 degrees
• The conversion site is at the left edge of the magnet, about 2 centimeters above the yoke.

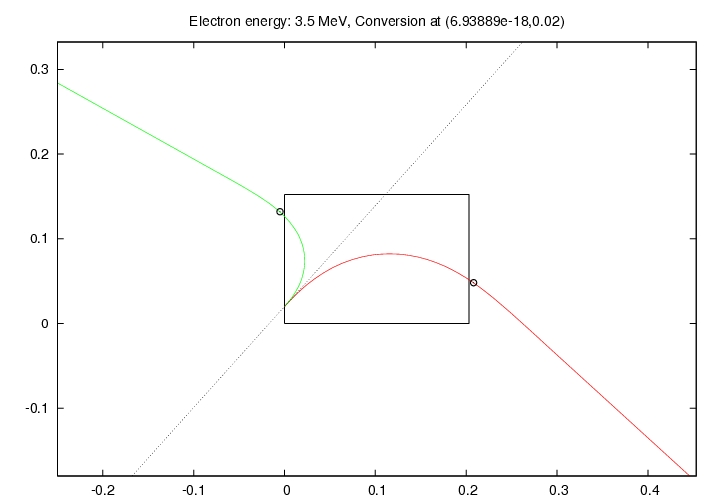
The figure below shows the trajectories of the electron (red) and the positron (green) for these parameters. The black box represents the magnet (with the return yoke at the bottom), and is roughly to scale. The dotted gray line represents the photon beam line.

One possible set of locations for the two detectors is to place one adjacent to the left edge of the magnet (left as seen in this graph) with the center at a distance of 0.132 meters above the yoke and displaced 0.005 cm from the left edge of the magnet. The other detector could have its center placed 0.005 meters from the right edge of the magnet and 0.048 meters above the return yoke. These suggested positions can be seen in the PDF document in the next section. Certainly, other positions would also work.

Pairs produced elsewhere on the beam

It is possible that the photons will pair produce in air at other locations on the beam, or that the electron produced will not carry 3.5 MeV of the total energy. This document shows the trajectories for the particles in these other scenarios. The electron energy and the "X" position of the conversion site are shown at the top of each graph. The black circles represent possible locations for the detectors. It appears that only the parameters described above will cause a coincidence in both detectors.