Difference between revisions of "DDP:Detailed Design Phase: Drawing and Assembly Package"
| Line 125: | Line 125: | ||
End plate was considered in 2D and 3D with various thicknesses and various materials, supports and constraints | End plate was considered in 2D and 3D with various thicknesses and various materials, supports and constraints | ||
| + | |||
| + | ==Point Load Deflection== | ||
| + | A simple back-of-the-envelope calculation for deflection was performed assuming aluminum endplates and a point-load force (representing the distributed force from the wires into a single load). The force on an endplate due only to the tension from the 4,928 wires is about 5700 N /2. A simple calculation based on the definition of Young's modulus can yield an order-of-magnitude-level estimate for the deflection of an aluminum endplate in which the wires exert a force perpendicular to the endplate. The deflection <math>y</math> of the endplate in terms of Young's Modulus <math>(Y)</math> is given by the equation: | ||
| + | |||
| + | :<math>Y \equiv \frac{F}{4wy} \left( \frac{l}{t}\right )^3</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>Y = 7 \times 10^{10}N/m^2 \equiv</math> Young's Modulus for Aluminum | ||
| + | :<math>F = 2850 N \equiv</math>point force/load | ||
| + | :<math>w =0.526 m \equiv</math> width of the endplate | ||
| + | :<math>y \equiv</math> deflection of endplate due to point force | ||
| + | :<math>l =4.02 m \equiv</math> length of the endplate | ||
| + | :<math>t = 0.05 m \equiv</math> thickness of the endplate | ||
| + | |||
| + | By substituting in the above values and solvign the equation, a deflection of 7 mm is expected for a 5 cm thick aluminum endplate. If a 5 cm thick stainless steel <math>(Y=2.1 \times 10^{11} N/m^2 )</math> endplate were used, the deflection would decrease from 7 mm to 2.5 mm (due to the linear dependence of the deflection on the Young's Modulus). The previous work performed by Kevin Folkman at the IAC came to a similar conclusion. | ||
| + | |||
| + | ==Distributed Load Deflection== | ||
| + | |||
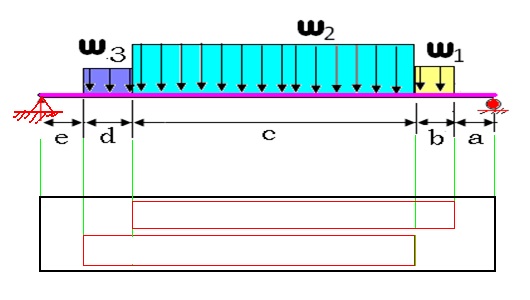
| + | The endplate deflection calculations were refined to a more realistic case in which the load is distributed evenly along the endplate. The tension of the wires on the endplate was divided into three regions; W1,W2, and W3. As shown in Figure 3.3.1, the load W3 corresponds to a region along the endplate in which wires from both super layers are creating a load on the endplate. Loads W1 and W2 represent regions in which only a single super layer is causing a load. The endplate is "simply" supported in order to calculate the deflection. The term "simply supported" implies that one side (left side of an endplate for this case) may rotate but not translate (resulting in two reaction forces) whereas the other side (the right side of and endplate for this case) is supported such that it may rotate and translate (resulting in a single, normal reaction force). Figure 7 labels the loads as well as distances over which the loads are applied on the end plate. A total force of 340 lbs exerted by the drift chamber wires is decomposed into its components according to the angle made by the wire on the endplate. | ||
| + | |||
| + | {| align="center" border="0" | ||
| + | |- | ||
| + | |[[Image:EndPlateDeflectionHandCalc.jpg]] | ||
| + | || | ||
| + | {| border="1" |cellpadding="20" cellspacing="0 | ||
| + | |- | ||
| + | |Label|| value | ||
| + | |- | ||
| + | | a|| 99.02 mm | ||
| + | |- | ||
| + | | b|| 96.22 mm | ||
| + | |- | ||
| + | | c|| 4025.88 mm | ||
| + | |- | ||
| + | | d|| 335.17 mm | ||
| + | |- | ||
| + | | e|| 273.88 mm | ||
| + | |- | ||
| + | | <math>W_1</math>|| 0.3=1223/(C+B) N/mm | ||
| + | |- | ||
| + | | <math>W_2</math>|| 0.61 N/mm | ||
| + | |- | ||
| + | | <math>W_3</math>|| 0.32 =1381/(C+D)N/mm | ||
| + | |||
| + | |} | ||
| + | |- | ||
| + | |Figure 3.3.1: A diagram of the loads on a simply supported endplate. The table to the right gives the load values and distances. | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | The following calculations are in accordance to a standard approach covered in all undergraduate "Mechanics of Materials" engineering courses. This method is based on integrating the elastic curve equation for a beam. The equation of the elastic curve relates deflection (y) to Moments (M) at given linear locations along the beam (x): | ||
| + | |||
| + | |||
| + | :<math>\frac{d^2y}{dx^2} = \frac{M(x)}{E I_A}</math> | ||
| + | |||
| + | |||
| + | where <math>E</math> represents Young's Modulus and <math>I_A</math> is the Area Momentum of Inertia. The Area Moment of Inertis <math>(I_A)</math> is defined as the second moment of an area about a given axis: | ||
| + | |||
| + | |||
| + | :<math>I_{A,x} = \int x^2 dA =</math> Area moment of inertia about the x-axis. | ||
| + | |||
| + | |||
| + | The mass moment of Inertia is defined as: | ||
| + | |||
| + | |||
| + | :<math>I= \int r^2 dM = \rho I_A</math> | ||
| + | |||
| + | |||
| + | In order to perform these calcuations, the following assumption were made: | ||
| + | |||
| + | # The end plate is made of homogenous uniform elastic material with a Young's Modulus of <math>E=210 x 10^23 N/mm^2</math> (Stainless Steel). | ||
| + | # The horizontal component of the loading is completely neglected. | ||
| + | # The deflection in the x-direction is negligible. | ||
| + | # The end plate is rectangular in shape with a width of 526 mm and thickness of 50.8 mm resulting area moment of inertia (<math>I_A</math>) =5746.4 <math>mm^4</math>. | ||
| + | # The loading provided by wire tensions are equivalent to a uniformly distributed load. | ||
| + | # The maximum deflection occurs along the length which is represented by <math>c</math> in the diagram. | ||
| + | # The loading applied is under the elastic limit of the material. | ||
| + | # The effects of the endplate weight are ignored. | ||
| + | |||
| + | The moments experienced along the endplate may be divided into 5 separate equations, each equation valid only for its corresponding region: | ||
| + | |||
| + | |||
| + | :<math>M_a = -\frac{W_1 \cdot b + W_2 \cdot c + W_3 \cdot d}{2} \cdot x</math> | ||
| + | :<math>M_b = -\frac{W_1 \cdot b + W_2 \cdot c + W_3 \cdot d}{2} \cdot (a+x) + \frac{W_1 \cdot x^2}{2}</math> | ||
| + | :<math>M_c = -\frac{W_1 \cdot b + W_2 \cdot c + W_3 \cdot d}{2} \cdot (a+b+x) + W_1 \cdot b \left ( \frac{b}{2} +x \right) + \frac{W_2 \cdot x^2}{2}</math> | ||
| + | :<math>M_d = -\frac{W_1 \cdot b + W_2 \cdot c + W_3 \cdot d}{2} \cdot (a+b+c+ x) + W_1 \cdot b \left ( \frac{b}{2} +c+x \right) + W_2\cdot c \left ( \frac{c}{2} + x \right) + \frac{W_3 \cdot x^2}{2}</math> | ||
| + | :<math>M_e = -\frac{W_1 \cdot b + W_2 \cdot c + W_3 \cdot d}{2} \cdot (a+b+c+d+ x) + W_1 \cdot b \left ( \frac{b}{2} +c+d+x \right) + W_2\cdot c \left ( \frac{c}{2} + d+x \right) + W_3 \cdot d \left (\frac{d}{2} +x \right)</math> | ||
| + | |||
| + | where <math>x</math> represents the linear distance along the endplate. If we assume that the largest magnitude of deflection occurs in region c, then we may integrate the above 2nd order elastic curve equation once and determine the critical point which represents the point of maximum deflection ( contra flexure). | ||
| + | |||
| + | :<math>\int \frac{dy}{dx}dy = \frac{dy}{dx} = \int M_c dx</math> | ||
| + | |||
| + | := <math>-\frac{W_1 \cdot b + W_2 \cdot c + W_3 \cdot d}{2} \cdot (ax+bx+x^2/2) + W_1 \cdot b \left ( \frac{bx}{2} +x^2/2 \right) + \frac{W_2 \cdot x^3}{6} +C_{integration}</math> | ||
| + | |||
| + | where <math>C_{integration} =</math> a constant of integration. Integrating the equation a 2nd time will result in an equation for the amount of the deflection. The constants of integration my be found by applying boundary conditions at points where the deflection is zero (at the ends or <math>x=0</math> and <math>x=L</math>). | ||
| + | |||
| + | Setting <math>\frac{dy}{dx}</math> to zero and solving for x gives the linear distance corresponding to the point of maximum deflection of x = 1654.96 mm. In other words, the maximum deflection occurs 1654.96 mm from region <math>b</math> of the endplate or <math>1654.96 + b + a = 1850.2</math> mm from the right hand side of the endplate. Substituting the value of x above results in a maximum deflection of 2.2 mm. Note, this deflection is only slightly smaller than that found with a point load assumption and a stainless steel endplate (2.2 mm compared to 2.5 mm, respectively). | ||
| + | |||
| + | ==Distributed Load FEA== | ||
| + | |||
| + | A Finite Element Analysis (FEA) was performed on the same stainless steel endplate design using the commercially available computer software ANSYS. For this analysis, the loading shown previously in the "Distrubuted Load" section was used. The maximum deflection observed from the FEA was 2.14 mm, as shown in Figure 3.4.1; this value differs from the hand calculation by only 3%. In addition to validating the FEA analysis with hand calculations, the above results also reveal the challenge of reducing the endplate deflection using stiffer materials due to an essentially linear dependence of the deflection on the Young's Modulus. The cubic dependence of the deflection on the thickness <math>(t)</math> of the endplate, however, can be used to reach the minimum endplate deflection criteria of 50 <math>\mu m</math>, in addition to the us of stiffer material. Increasing the endplate thickness, however, comes at the cost of increasing the end plate mass. As a result, composite materials were considered in order to minimize weight. The performance of these composite materials is shown in the 3-D model section of this report. | ||
| + | |||
| + | {| align="center" border="0" | ||
| + | |- | ||
| + | |[[Image:EndPlateDeflection_5cmx53cmx4m_ThickStainlessSteel.jpg]] | ||
| + | |- | ||
| + | | Figure 3.4.1: ANSYS FEA results for deflection of a stainless steel endplate design for a distrubed loading. | ||
| + | |} | ||
| + | |||
| + | ==Composite End Plate == | ||
| + | === Effective Young's Modulus <math>Y_{eff}</math>=== | ||
| + | The R3 endplates used in the CLAS 6 GeV detector were comprised of a polyeurethane foam core 50.8 mm thick (2 inches) with 1.2 mm thick (0.048 inch) stainless steel sheets epoxied to each side, as shown in Figure 3.5.1. | ||
| + | {| align="center" border="0" | ||
| + | |- | ||
| + | |[[Image:EndPlateMaterialDimensions.jpg]] | ||
| + | |- | ||
| + | | Figure 3.5.1: Polyeurethane foam/stainless steel composite endplate construction and dimensions. | ||
| + | |} | ||
| + | |||
| + | |||
| + | An effective Young's Modulus (<math>Y_{eff}</math>) was used in the FEA model in order to simplify the model. The effective Young's Modulus for this endplate, weighted by the volume of each plate, is | ||
| + | |||
| + | :<math>Y_{eff} = \frac{V_p Y_p + V_s Y_s }{V_{tot}}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>Y_p = 1.4 \times 10^8 N/m^2</math> | ||
| + | :<math>Y_s = 2.1 \times 10^{11} N/m^2</math> | ||
| + | :<math>V_p = L \times W \times 2</math> inches | ||
| + | :<math>V_s = L \times W \times 0.096</math> inches | ||
| + | |||
| + | |||
| + | Therefore, the effective Young's Modulus was found to be: | ||
| + | |||
| + | : <math>Y_{eff} = \frac{2(1.4 \times 10^8) +0.096(2.1 \times 10^{11})}{2.096} = 9.75 \times 10^{9} N/m^2</math> | ||
| + | |||
| + | === FEA Deflection Results=== | ||
| + | The effective Young's Modulus of <math>9.75 \times 10^9 N/m^2</math> was used to determine the deflection of the endplate due to a distributed load (see Figure 3.5.2). Results indicate a maximum transverse deflection of 32.4 mm which is larger than that observed with the stainless steel material. However, when gravity is included, the composite material will deflect less due to its lower density. | ||
| + | |||
| + | {| align="center" border="0" | ||
| + | |- | ||
| + | |[[Image:DtotNoRods.jpg]] | ||
| + | || | ||
| + | {| align="center" border="1" | ||
| + | |- | ||
| + | | Configuration || X max || Y max || Z max || D max | ||
| + | |- | ||
| + | | || (mm) || (mm) || (mm)|| (mm) | ||
| + | |- | ||
| + | | No rods ||.67 || 32.4|| .04 || 32.4 | ||
| + | |} | ||
=====Fixed Carbon Rod locations===== | =====Fixed Carbon Rod locations===== | ||
Revision as of 08:29, 17 July 2008
Detailed Design Drawing Report 6/27/08
Outline:
1.) Dimensions
2.) Constraints: Case 3 from progress report: constrain triangle and nose plate on upstream side.
3.) Deflection Analysis
Steps:
a.) check triangle contact region and its mass b.) add another carbon fiber rod c.) increase size of back plate
4.) Drawings
drawings in PDF format
a.) Endplate structural drawing (no holes just shaded area)
b.) Drawings for all other parts
c.)
d.) Copy old R3 (take advantage of no curved window.
Report
Introduction
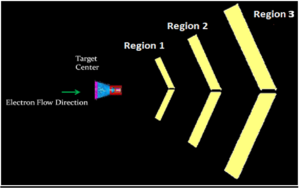
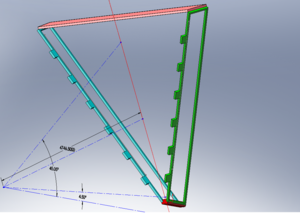
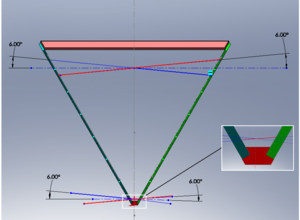
The CLAS12 Drift chamber has 3 regions arranged as shown below
The electrons released from the target center will flow through region 1, region 2 and region 3. All these regions look the same way. However, their sizes and the materials with which they are made are different. Due to the fact their sizes are different; some of them have some structural add-ons to support their structural abilities. The chambers are arranged in such a way that every chamber receives the same number of electrons. Apart from that, the chambers were shaped in such a way that all the electrons travel approximately the same distance before they hit a particular chamber.
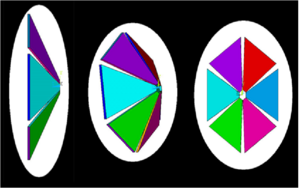
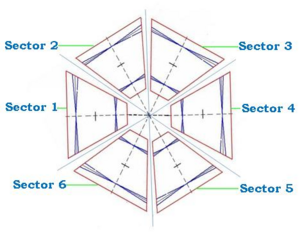
Each and every chamber has 6 equal sized pieces which are shaped similar to a triangular piece. All of these pieces are arranged and bowed inward to resemble sectors in a 6 sector umbrella.As discussed before, each region will be sized different. Region 3 will be the biggest of all, as region 3 has to cover a larger electron span (surface area).
Although these pieces are termed as triangular, these are not triangular in reality. The nose which is the smallest of all is very small compared to the other plates, which will make us to visualize this as a triangular piece. Ar Co2 (90/10) gas is maintained in each of these chambers at an operating pressure of 0.001444 Psi and a peak pressure 5 times higher. In turn there are about 4928 very sensitive wires (112 Sense wires with 44 Wire Layers) connected across the plates inside each piece.
Design Criteria
Initial parameters to be followed to fulfill to satisfy design Criteria
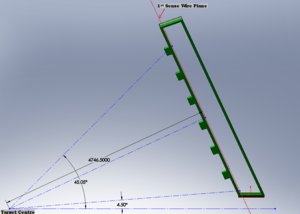
1. Distance from target to first sense wire plane along a ray which is normal to the end plate = 4746.5 mm
2. Chamber Tilt Angle = 25 Degrees
3. Maximum Scattering Angle = 45.05 Degrees
4. Minimum Scattering Angle = 4.5 Degrees
5. Wires are at 6 Degrees to the horizontal in each of its wire planes
Wire pattern
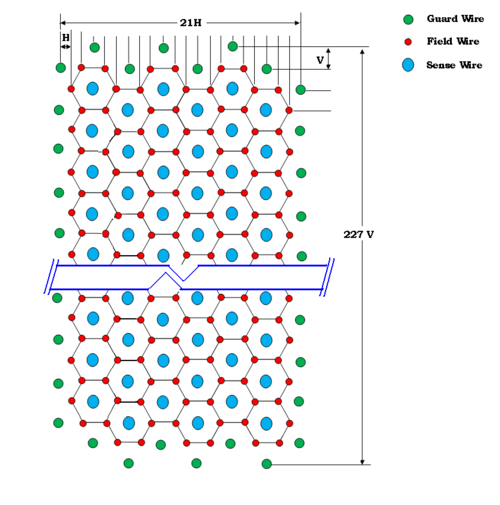
The wire pattern at the center plane will be symmetric and easy to understand. The wire pattern in each super layer on this plane is same and a view at this wires at this plane will be as follows
In the horizontal direction we have 6 six sense wires. so, there will be a 2 + 6 times 3 + 2 = 22 wire planes as shown in the fig. If the distance between each wire plane is 'H' mm. Then the total span of wires in this direction will be 21H mm.
In the vertical direction, there are 112 sense wires, so there will be 2 + 112 + 2 = 116 wire planes as shown. If the distance between each wire plane is 'V' mm. Then, the total span in this direction will be 115V mm
H = ?
V = ?
No. of sense wires in each super layer = ?
No. of field wires in each super layer = ?
No. of guard wires in each super layer = ?
Introduction to Assembly
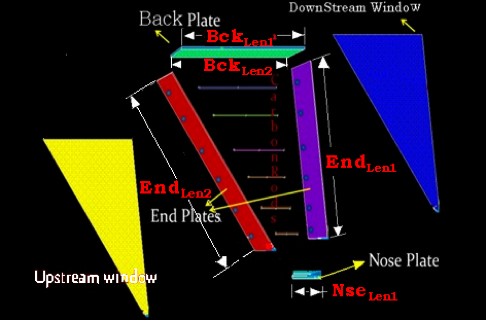
Nose Plate will be made of rigid material such as solid aluminum, since the supporting mechanism will be attached to these plates. The nose plate will connect the bottoms of the two end plated and provides the interface.
The End plate is about 4830 mm and 4665mm in length along the longitudinal length and about 525mm in width. It has approximately about 5000 holes with an approximate diameter of 6mm on the surface and about 9mm inside the surface. There will be two End plates names as Right End plate and Left End plate which are located to the actual right and left side of each sector when viewed from the target center respectively.
Back Plate:  It is the plate which connects the top edges of both the end plates and holds the fixtures settings
It is the plate which connects the top edges of both the end plates and holds the fixtures settings
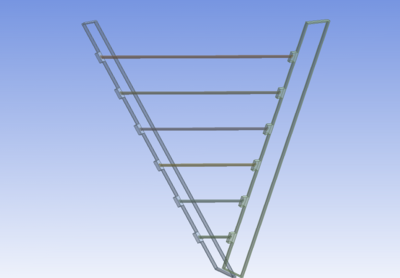
To provide rigidity, there will be several carbon rods fixed in between both the end plates and they vary in length depending on no.of carbon rods used and the location of rods. These rods are hollow to reduce the electron dissipation in the section.
Upstream Window and Downstream Window's:
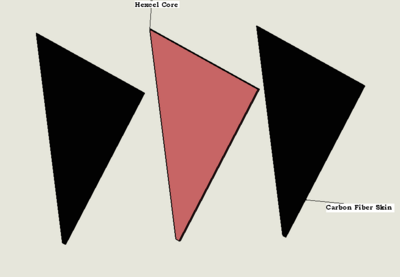
Upstream Window is the thin Mylar sheet of about 1/1000th of an inch crimped or glued on the upstream side of electron flow slightly after the carbon rods. Downstream Window is a Hexcel honeycomb material provided on the downstream side to help support the assembly, to provide rigidity and to enclose each sector
Analysis
To determine the stability of the design, various sets of analysis were performed under different constraint and loading conditions. Sometimes each of the part was analyzed individually and also in the assembly. Some parts were analyzed for different materials
Part Analysis
These are those analysis were individual parts were analyzed under various loading and constraint conditions. Some of the constraints were assumed to understand the influence of each constraint, material and load. supportive manual calculations were also compared with these analysis in few cases.
End Plate
End plate was considered in 2D and 3D with various thicknesses and various materials, supports and constraints
Point Load Deflection
A simple back-of-the-envelope calculation for deflection was performed assuming aluminum endplates and a point-load force (representing the distributed force from the wires into a single load). The force on an endplate due only to the tension from the 4,928 wires is about 5700 N /2. A simple calculation based on the definition of Young's modulus can yield an order-of-magnitude-level estimate for the deflection of an aluminum endplate in which the wires exert a force perpendicular to the endplate. The deflection of the endplate in terms of Young's Modulus is given by the equation:
where
- Young's Modulus for Aluminum
- point force/load
- width of the endplate
- deflection of endplate due to point force
- length of the endplate
- thickness of the endplate
By substituting in the above values and solvign the equation, a deflection of 7 mm is expected for a 5 cm thick aluminum endplate. If a 5 cm thick stainless steel endplate were used, the deflection would decrease from 7 mm to 2.5 mm (due to the linear dependence of the deflection on the Young's Modulus). The previous work performed by Kevin Folkman at the IAC came to a similar conclusion.
Distributed Load Deflection
The endplate deflection calculations were refined to a more realistic case in which the load is distributed evenly along the endplate. The tension of the wires on the endplate was divided into three regions; W1,W2, and W3. As shown in Figure 3.3.1, the load W3 corresponds to a region along the endplate in which wires from both super layers are creating a load on the endplate. Loads W1 and W2 represent regions in which only a single super layer is causing a load. The endplate is "simply" supported in order to calculate the deflection. The term "simply supported" implies that one side (left side of an endplate for this case) may rotate but not translate (resulting in two reaction forces) whereas the other side (the right side of and endplate for this case) is supported such that it may rotate and translate (resulting in a single, normal reaction force). Figure 7 labels the loads as well as distances over which the loads are applied on the end plate. A total force of 340 lbs exerted by the drift chamber wires is decomposed into its components according to the angle made by the wire on the endplate.
The following calculations are in accordance to a standard approach covered in all undergraduate "Mechanics of Materials" engineering courses. This method is based on integrating the elastic curve equation for a beam. The equation of the elastic curve relates deflection (y) to Moments (M) at given linear locations along the beam (x):
where represents Young's Modulus and is the Area Momentum of Inertia. The Area Moment of Inertis is defined as the second moment of an area about a given axis:
- Area moment of inertia about the x-axis.
The mass moment of Inertia is defined as:
In order to perform these calcuations, the following assumption were made:
- The end plate is made of homogenous uniform elastic material with a Young's Modulus of (Stainless Steel).
- The horizontal component of the loading is completely neglected.
- The deflection in the x-direction is negligible.
- The end plate is rectangular in shape with a width of 526 mm and thickness of 50.8 mm resulting area moment of inertia () =5746.4 .
- The loading provided by wire tensions are equivalent to a uniformly distributed load.
- The maximum deflection occurs along the length which is represented by in the diagram.
- The loading applied is under the elastic limit of the material.
- The effects of the endplate weight are ignored.
The moments experienced along the endplate may be divided into 5 separate equations, each equation valid only for its corresponding region:
where represents the linear distance along the endplate. If we assume that the largest magnitude of deflection occurs in region c, then we may integrate the above 2nd order elastic curve equation once and determine the critical point which represents the point of maximum deflection ( contra flexure).
- =
where a constant of integration. Integrating the equation a 2nd time will result in an equation for the amount of the deflection. The constants of integration my be found by applying boundary conditions at points where the deflection is zero (at the ends or and ).
Setting to zero and solving for x gives the linear distance corresponding to the point of maximum deflection of x = 1654.96 mm. In other words, the maximum deflection occurs 1654.96 mm from region of the endplate or mm from the right hand side of the endplate. Substituting the value of x above results in a maximum deflection of 2.2 mm. Note, this deflection is only slightly smaller than that found with a point load assumption and a stainless steel endplate (2.2 mm compared to 2.5 mm, respectively).
Distributed Load FEA
A Finite Element Analysis (FEA) was performed on the same stainless steel endplate design using the commercially available computer software ANSYS. For this analysis, the loading shown previously in the "Distrubuted Load" section was used. The maximum deflection observed from the FEA was 2.14 mm, as shown in Figure 3.4.1; this value differs from the hand calculation by only 3%. In addition to validating the FEA analysis with hand calculations, the above results also reveal the challenge of reducing the endplate deflection using stiffer materials due to an essentially linear dependence of the deflection on the Young's Modulus. The cubic dependence of the deflection on the thickness of the endplate, however, can be used to reach the minimum endplate deflection criteria of 50 , in addition to the us of stiffer material. Increasing the endplate thickness, however, comes at the cost of increasing the end plate mass. As a result, composite materials were considered in order to minimize weight. The performance of these composite materials is shown in the 3-D model section of this report.
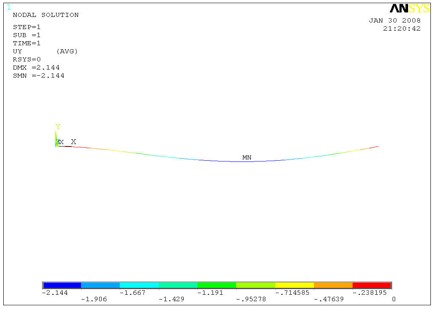
|
| Figure 3.4.1: ANSYS FEA results for deflection of a stainless steel endplate design for a distrubed loading. |
Composite End Plate
Effective Young's Modulus
The R3 endplates used in the CLAS 6 GeV detector were comprised of a polyeurethane foam core 50.8 mm thick (2 inches) with 1.2 mm thick (0.048 inch) stainless steel sheets epoxied to each side, as shown in Figure 3.5.1.
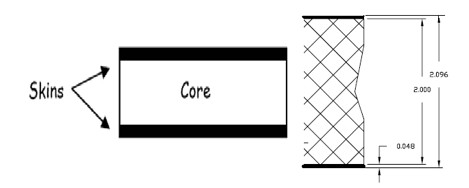
|
| Figure 3.5.1: Polyeurethane foam/stainless steel composite endplate construction and dimensions. |
An effective Young's Modulus () was used in the FEA model in order to simplify the model. The effective Young's Modulus for this endplate, weighted by the volume of each plate, is
where
- inches
- inches
Therefore, the effective Young's Modulus was found to be:
FEA Deflection Results
The effective Young's Modulus of was used to determine the deflection of the endplate due to a distributed load (see Figure 3.5.2). Results indicate a maximum transverse deflection of 32.4 mm which is larger than that observed with the stainless steel material. However, when gravity is included, the composite material will deflect less due to its lower density.
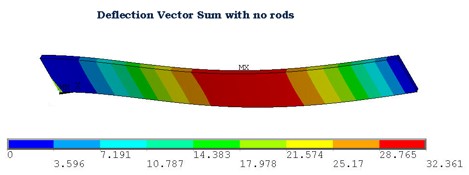
|
Fixed Carbon Rod locationsIn this analysis, the end plate is a straight rectangular shaped sheet. six carbon rods were assumed and the locations where the carbon rods are attached to the end plate are fixed for analysis. FR-3700 Foam with slices of steel is considered for this analysis. Effective Material properties were used wherever required. The short sided edges of the rectangular end plate is considered to be fixed pretending a cantilever beam. DrawingsThe Assembly of each sector in the region 3 drift chamber can be considered similar to each other. Each assembly can be divided into sub-assemblies like 1. Nose Plate 2. Right End Plate 3. Left End plate 4. Back plate 5. Backing Sheet 6. Carbon rods 7. Attachments: These are the external geometric parts of each sector, used for clamping and mounting each sector. so, they might change with the orientation of each sector A detailed drawing of this Basic sector assmebly can be viewed at File:B00000-01-10-0001.pdf
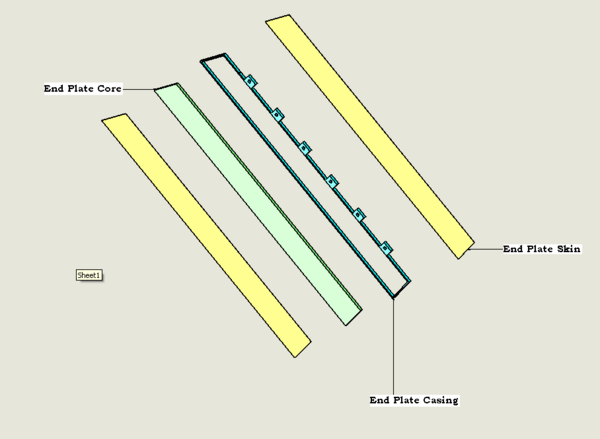
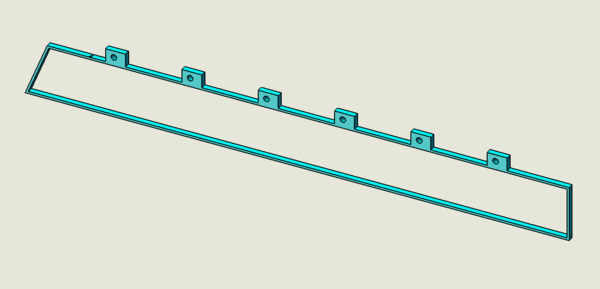
Nose PlateNose plate is the plate where both the end plates are attached to it on either side A detailed drawing of Nose plate can be viewed at File:B00000-01-10-0002.pdf Right end plateLeft end plate is the end plate to the left hand side if we are viewing from the target. They can be referenced with left and right to show each sub assembly. A detailed drawing of right end plate Core can be viewed at File:B00000-01-10-0003.pdf A detailed drawing of right end plate skin can be viewed at File:B00000-01-10-0004.pdf Since end plate casing will not have holes for wires, the drawing for left end plate casing and right end plate casing will be the same. A detailed drawing of End plate casing can be viewed at File:B00000-01-10-0005.pdf Left End PlateLeft end plate is the end plate to the left hand side if we are viewing from the target. Left end plate and the right end plate are same with parts and its dimensions. However, the hole locations differ between each other. Each end plate sub assembly consists of 3 parts, namely End plate casing - Made of Aluminum.
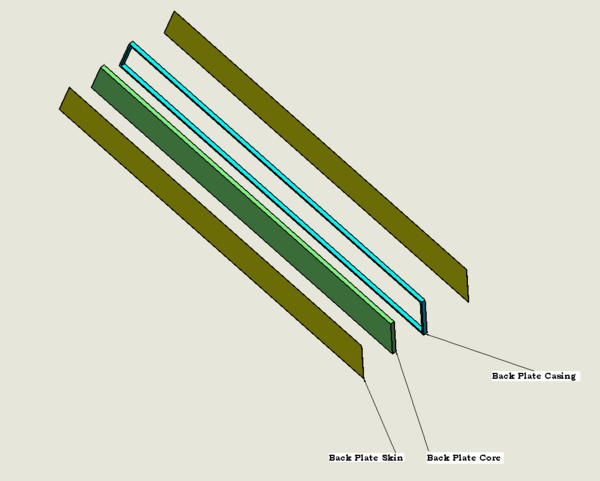
A detailed drawing of Left end plate Core can be viewed at File:B00000-01-10-0006.pdf A detailed drawing of Left end plate skin can be viewed at File:B00000-01-10-0007.pdf Back PlateBack plate is the plate which connects the left end plate and right end plate on the top. Back plate sub assembly consists of 3 parts, namely Back plate Core - made of Polyurethane Back plate Skins - 2 No's- Made of stainless steel Back plate casing - Made of Aluminum A detailed drawing of back plate Core can be viewed at File:B00000-01-10-0008.pdf A detailed drawing of back plate skin can be viewed at File:B00000-01-10-0009.pdf A detailed drawing of back plate casing can be viewed at File:B00000-01-10-0010.pdf Backing SheetBacking sheet is the large sheet which is mounted on the downstream side of sector. It consists of 2 parts, namely Hexcel Core and Carbon fiber skins on either side A detailed drawing of back plate Core can be viewed at File:B00000-01-10-0011.pdf A detailed drawing of back plate skin can be viewed at File:B00000-01-10-0012.pdf Carbon fiber rodsThese rods are mounted on the upstream side of each sector, connecting the left end plate aluminum casing and right end plate aluminum casing.. There are 6 Carbon rods each of outer diameter of 50.8 mm and inner diameter of 48.26mm A detailed drawing of carbon fiber rods can be viewed at File:B00000-01-10-0013.pdf
|