|
|
| Line 1: |
Line 1: |
| | + | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] |
| | + | |
| | + | |
| | We're looking to see which is better for letting photons through, Carbon or Aluminum. | | We're looking to see which is better for letting photons through, Carbon or Aluminum. |
| | | | |
| Line 106: |
Line 109: |
| | | | |
| | [[Image:carbon_plot.jpg]] | | [[Image:carbon_plot.jpg]] |
| | + | |
| | + | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] |
Go Back
We're looking to see which is better for letting photons through, Carbon or Aluminum.
20 MeV for Carbon
range is [math]10.49 \frac{g}{cm^{3}}[/math]
density of Carbon = [math]~2.3 \frac{g}{cm^{3}}[/math]
thickness = [math]\frac{range}{density} = \frac{10.49}{2.3} = 4.56 cm[/math]
Therefore, the thickness of our Carbon is 4.56 cm
10 MeV hitting 4.56 cm of Carbon
n = [math]2.3 \frac{g}{cm^{3}} \times \frac{6.022 \cdot 10^{23} atoms}{12 g} = 1.2 \cdot 10^{23} \frac{atoms}{cm^{3}}[/math]
σ = [math].4 \cdot 10^{-24} cm^{2}[/math]
nσt = [math]1.2 \cdot 10^{23} \frac{atoms}{cm^{3}} \times .4 \cdot 10^{-24} cm^{2} \times 4.56 cm = .218[/math]
[math]\,\!\, e^{-n \sigma t} =\gt e^{-.218} = .80 =\gt 80%[/math] of the photons get through the Carbon
What about Aluminum?
20 MeV for Aluminum
range is [math]10.54 \frac{g}{cm^{3}}[/math]
density of Carbon = [math]2.7 \frac{g}{cm^{3}}[/math]
thickness = [math]\frac{range}{density} = \frac{10.54}{2.7} = 3.9 cm[/math]
Therefore, the thickness of our Aluminum is 3.9 cm
10 MeV hitting 3.9 cm of Aluminum
n = [math]2.7 \frac{g}{cm^{3}} \times \frac{6.022 \cdot 10^{23} atoms}{27 g} = 6.022 \cdot 10^{22} \frac{atoms}{cm^{3}}[/math]
σ = [math]1.039 \cdot 10^{-24} cm^{2}[/math]
nσt = [math]6.022 \cdot 10^{22} \frac{atoms}{cm^{3}} \times 1.039 \cdot 10^{-24} cm^{2} \times 3.9 cm = .24[/math]
[math]\,\!\, e^{-n \sigma t}=e^{-.24}=.79=\gt 79%[/math] of the photons get through the Aluminum
Since more gets through Carbon, we're going to forget about Aluminum and focus solely on using Carbon.
So, we're keeping the same information for the 20 MeV for Carbon and calculate the rest of the information for 6, 8, 12, 13, and 14 MeV.
6 MeV hitting 4.56 cm of Carbon
n = [math]2.3 \frac{g}{cm^{3}} \times \frac{6.022 \cdot 10^{23} atoms}{12 g} = 1.2 \cdot 10^{23} \frac{atoms}{cm^{3}}[/math]
σ = [math]4.924 \cdot 10^{-25} cm^{2}[/math]
nσt = [math]1.2 \cdot 10^{23} \frac{atoms}{cm^{3}} \times 4.924 \cdot 10^{-25} cm^{2} \times 4.56 cm = .269[/math]
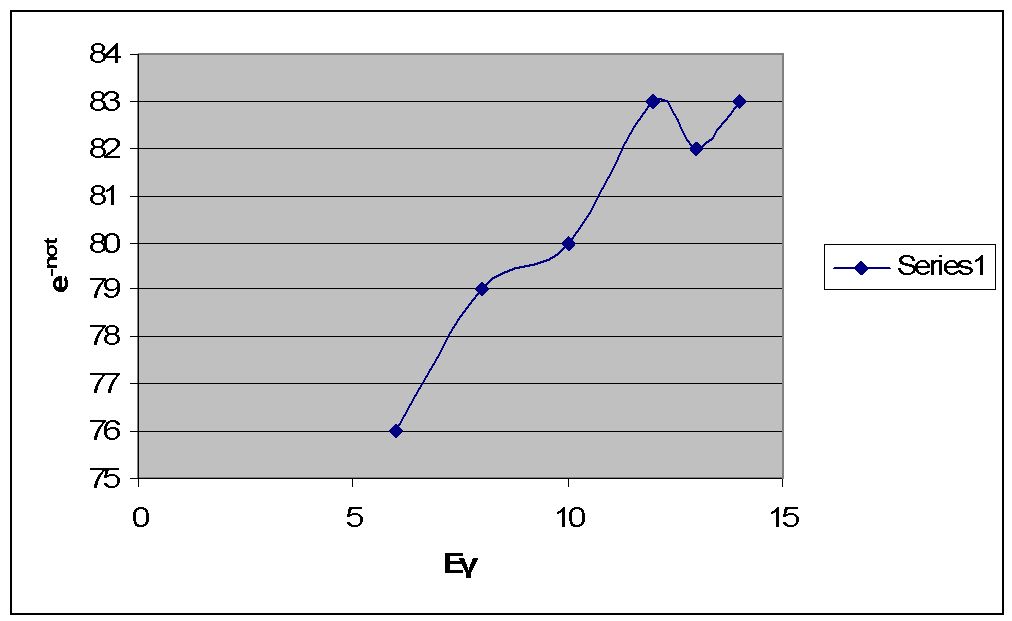
[math]\,\!\, e^{-n \sigma t} =\gt e^{-.269} = .76 =\gt 76%[/math] of the photons get through the Carbon
8 MeV hitting 4.56 cm of Carbon
n = [math]2.3 \frac{g}{cm^{3}} \times \frac{6.022 \cdot 10^{23} atoms}{12 g} = 1.2 \cdot 10^{23} \frac{atoms}{cm^{3}}[/math]
σ = [math]4.297 \cdot 10^{-25} cm^{2}[/math]
nσt = [math]1.2 \cdot 10^{23} \frac{atoms}{cm^{3}} \times 4.297 \cdot 10^{-25} cm^{2} \times 4.56 cm = .235[/math]
[math]\,\!\, e^{-n \sigma t} =\gt e^{-.235} = .79 =\gt 79%[/math] of the photons get through the Carbon
12 MeV hitting 4.56 cm of Carbon
n = [math]2.3 \frac{g}{cm^{3}} \times \frac{6.022 \cdot 10^{23} atoms}{12 g} = 1.2 \cdot 10^{23} \frac{atoms}{cm^{3}}[/math]
σ = [math]3.646 \cdot 10^{-25} cm^{2}[/math]
nσt = [math]1.2 \cdot 10^{23} \frac{atoms}{cm^{3}} \times 3.646 \cdot 10^{-25} cm^{2} \times 4.56 cm = .199[/math]
[math]\,\!\, e^{-n \sigma t} =\gt e^{-.199} = .83 =\gt 83%[/math] of the photons get through the Carbon
13 MeV hitting 4.56 cm of Carbon
n = [math]2.3 \frac{g}{cm^{3}} \times \frac{6.022 \cdot 10^{23} atoms}{12 g} = 1.2 \cdot 10^{23} \frac{atoms}{cm^{3}}[/math]
σ = [math]3.545 \cdot 10^{-25} cm^{2}[/math]
nσt = [math]1.2 \cdot 10^{23} \frac{atoms}{cm^{3}} \times 3.545 \cdot 10^{-25} cm^{2} \times 4.56 cm = .194[/math]
[math]\,\!\, e^{-n \sigma t} =\gt e^{-.194} = .82 =\gt 82%[/math] of the photons get through the Carbon
14 MeV hitting 4.56 cm of Carbon
n = [math]2.3 \frac{g}{cm^{3}} \times \frac{6.022 \cdot 10^{23} atoms}{12 g} = 1.2 \cdot 10^{23} \frac{atoms}{cm^{3}}[/math]
σ = [math]3.461 \cdot 10^{-25} cm^{2}[/math]
nσt = [math]1.2 \cdot 10^{23} \frac{atoms}{cm^{3}} \times 3.461 \cdot 10^{-25} cm^{2} \times 4.56 cm = .189[/math]
[math]\,\!\, e^{-n \sigma t} =\gt e^{-.189} = .83 =\gt 83%[/math] of the photons get through the Carbon
Go Back
