Forest RC circuits

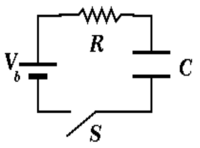
The circuit diagram below defines a common circuit known as an RC circuit. The circuit involves only a capacitor and a resistor. The resistors role is to impede (resist) the flow of current (iR) and the capacitors role is to store charge (q/C).

Pumping air into a bicycle tire is a fair analogy of this circuits properties. You are the battery, the pump you push is the resistor and the tire is the capacitor. As a battery you push electrons through the resistor (pump) and into the capacitor. The resistor (pump) resists the flow of the electrons into the capacitor. As the capacitor starts to charge up (tire fills with air) it becomes harder to push electrons onto the capacitors plates (add air to the tire). Now the capacitor (tire) starts to resist you pumping making it harder to charge up.

Discharging RC circuit

Let's first describe what happens when a fully charged capacitor is allowed to discharge (You pumped up your bike tire but you forgot to put the stem in the valve and all the air starts leaking out when you take off the pump). Assume we left the battery connected to the above circuit for an infinite amount of time.

If we apply Kirchhoff's loop Theorem by starting at the location of the battery and go around clockwise we would write

[math]V_b - IR - \frac{q}{C} = 0[/math]

If we then replaced the batteries EMF with a wire so it was no longer working to keep the charge on the capacitor. Then we would have the equation

[math]0 - IR - \frac{q}{C} = 0[/math]

[math]\Rightarrow R\frac{-dq}{dt} - \frac{1}{C} q = 0[/math]

[math]\Rightarrow \frac{-dq}{dt} - \frac{1}{RC} q = 0[/math]

Another way to arrive at the equation above is to think of the capacitor as being a charged up battery with a voltage of [math]\frac{q}{C}[/math] which is discharging with a current[math] I=-\frac{dq}{dt}[/math].

Then you would have

[math]IR-\frac{q}{C} = (-\frac{dq}{dt} ) R -\frac{q}{C} =0[/math]

The above is a first order differential equation which you can integrate directly

Quiz

Integrate the above differential equation for a discharging capacitor to determine the dependence of charge (q) with time (t). Which of the answers below looks most like yours.

A.) [math]ln(q) = \frac{-t}{RC}[/math] B.) [math]q^{-2} = \frac{-t}{RC}[/math] C.) [math]q^{-1} = \frac{-t}{RC}[/math] D.) [math]ln(q) = \frac{t}{RC}[/math]

Answer

Assume the capacitor has been charged up to a total charge Q

[math]\int_Q^q \frac{dq}{q} = - \int_0^t \frac{dt}{RC}[/math]

[math]\ln(q) - \ln(Q) = \frac{-1}{RC} (t-0)[/math]

[math]q = Qe^{-t/RC}[/math]

Charging RC circuit

Let's now assume we waited an infinite amount of time for the capacitor to discharge and we are interested in the charge as a function of time on the capacitor when we turn the battery back on.

Kirchhoff's Loop theorem with the battery inserted says

V_b -IR - \frac{q}{C} = 0

or

R \frac{dq}{dt} + \frac{q}{C} = V_b

the above differential equation is similar to the equation for a discharging capacitor except that instead of zero on the RHS we have the battery's voltage [math]V_b[/math].