Difference between revisions of "LB DetLimits Thesis"
| Line 109: | Line 109: | ||
[[File:A Mix Div a Pure NormCorrected Se81m NoFitRestrict.png|200px]] | [[File:A Mix Div a Pure NormCorrected Se81m NoFitRestrict.png|200px]] | ||
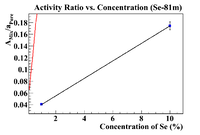
| − | The equation of the fit gives an initial concentration of (1.75 +/- 0.17)%, but I want to force the intercept to be greater than -0.1%, so force the fit | + | The equation of the fit gives an initial concentration of (1.75 +/- 0.17)%, but I want to force the intercept to be greater than -0.1%, so force the fit to have the desired intercept |
| + | |||
| + | [[File:A Mix Div a Pure NormCorrected Se81m FitRestrict.png|200px]] | ||
| + | |||
| + | Keeping the error in the y-intercept, the equation of the line is | ||
| + | |||
| + | <math> (0.0259648 \pm 0.00205475) + (0.259640 \pm 0.0000008)x | ||
Revision as of 21:38, 1 August 2018
50% Excluded
For this analysis, begin by using the first measurement of the Se-75 line and using the standard exponential decay equation to correct it and its error back to the time of beam off. Below is a table of the Se-75 (120d) corrected measurements as well as the front nickel foils and the Mn-54 data for each measurement. Note the Mn-54 analysis was weighted by the mass of the soil.
| Sample | Activated (total beam time) | Counted | Fully Thesis Corrected Rate @ 1st Measurement (Hz) | |
| 10% Se/Soil Mixture | 5/23/17 and 5/24/17 (83 min) | 07/18/17 (16:25:44) | 3109.68 95.39 | 4280.08 131.29 |
| 10% Se/Soil Pure Witness selenium | 5/23/17 and 5/24/17 (83 min) | 8/1/17 (16:05:51) | 4161.29 127.63 | 6210.50 190.48 |
| 10% Se/Soil Front Inner Ni Foil | 5/23/17 (1h) | 5/23/17 (15:52:21) | 385955 23488.8 | 425064.36 25868.95 |
| 10% Se/Soil Mixture Mn-54 | 5/23/17 (1h) | 07/18/17 (16:25:44) | 15.63 0.56 | 17.67 0.63 |
| 1% Sample Se/Soil Mixture | 5/23/17 (1h) | 6/23/17 (16:39:03) | 2233.33 68.52 | 2675.24 82.08 |
| 1% Sample Se/Soil Pure Witness selenium | 5/23/17 (1h) | 7/20/17 (16:39:46) | 3840.86 117.81 | 5379.43 165.00 |
| 1% Sample Se/Soil Front Inner Ni Foil | 5/23/17 (1h) | 5/23/17 (17:59:39) | 261461 16045.7 | 293170.78 17991.71 |
| 1% Sample Se/Soil Mixture Mn-54 | 5/23/17 (1h) | 6/23/17 (16:39:03) | 9.38 0.39 | 10.05 0.42 |
| 0.1% Sample Se/Soil Mixture | 5/23/17 (30 min) | 6/19/17 (18:25:18) | 849.46 26.07 | 993.59 30.49 |
| 0.1% Sample Se/Soil Pure Witness Selenium | 5/23/17 (30 min) | 07/25/17 (16:32:52) | 834.41 25.61 | 1201.58 36.88 |
| 0.1% Sample Se/Soil Front Inner Ni Foil | 5/23/17 (30 min) | 5/24/17 (14:25:39 | 118412 7280.06 | 197670.18 12152.98 |
| 0.1% Sample Se/Soil Mn-54 | 5/23/17 (30 min) | 6/19/17 (18:25:18) | 9.38 0.33 | 9.96 0.35 |
Mn-54 Efficiency
A calibrated Mn-54 source was used to find the efficiency of an 834 keV line. The source was serial #J4-348, which had an activity of 9.882 on 8/01/12, so the activity on 4/18/17 was
Now converting to Hz gives
| Source | Energy (keV) | Position | Expected Rate (Hz) | ROOT Window (keV) | HpGe Rate (Hz) | HpGe Detector A Efficiency (%) |
| Mn-54 (J4-348) | 834 | 10cm (Det A) | 8138.05 3\% | [829,839] | 25.87 0.28 | 0.32 0.01 |
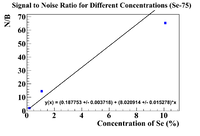
Activity Ratio Plots (Se-75)
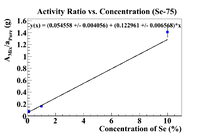
Below are plots of the activity ratio of the Se/Soil mixture and specific activity of the pure selenium pellet as a reference material. The plots also have no restrictions on the equation of the line.
Following the analysis in Nate's thesis, the initial concentration should be the intercept on the x-axis, which is
This is much more physical than previous answers, but I was able to detect Se-75 at a 0.1% level. Let's try some other reference materials
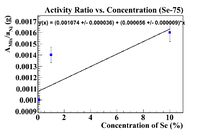
Below is a plot where the activity ratio was taken using Ni-57 as a reference material. This was the front inner Nickel foil
This is not very physical because the graph implies that the initial concentration in the soil was 19.18%, but there were no Se-75 lines observed in a pure soil sample, so this cannot be true
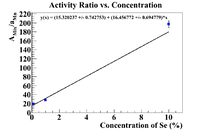
Finally let's try Mn-54 as a reference material as it was internal to the sample.
Now find the initial concentration by finding the x-intercept.
This is still better than the nickel, but still not physical because of the argument presented in the section about the pure selenium ratio.
Now try to fix the linear fit's parameters such that the x-intercept is less than 0.1%. To do this, fix the y-intercept and the slope separately to see if their intercepts agree. If y = A+Bx, when y = 0, then
The fitting function for the plot with the pure selenium used as a reference material was y(x) = (0.054558 +/- 0.004056) + (0.122961 +/- 0.006568)*x, so by fixing the y-intercept, we have
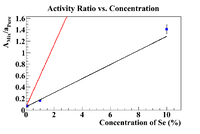
Below is a plot where the red line is the fixed and bounded fit
Even though the y-value was fixed, I kept the error so the fit equation is y(x) = (0.0545580 +/- 0.004056) + (0.545580 +/- 0.0000414)*x, which yields an x intercept of 0.1 +/-0.01 (note that for all plots it seems by bounding the fit the x-intercept will be as close as possible to the closest value before restrictions, so all fixed fits give x-intercepts of 0.1%
Now shift the concentration values by 0.1%, and plot the signal to noise ratio at the highest measured value.
Now we still have a non-zero y-intercept, but by increasing it by 2 standard deviations gives a value of 0.195189, now finding the value of x for this, we get
where the error is determined by
Where is the y intercept increased by 2 standard deviations
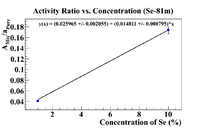
Activity Ratio Plots (Se-81m)
Let's repeat the above analysis with Se-81m data. So begin by plotting the ratio vs the concentration (omitting the 50% sample)
The equation of the fit gives an initial concentration of (1.75 +/- 0.17)%, but I want to force the intercept to be greater than -0.1%, so force the fit to have the desired intercept
Keeping the error in the y-intercept, the equation of the line is
<math> (0.0259648 \pm 0.00205475) + (0.259640 \pm 0.0000008)x