Difference between revisions of "Converting to barns"
| Line 51: | Line 51: | ||
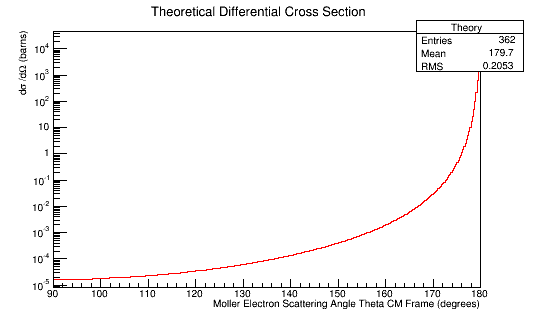
| − | [[File:Theory_new.png|frame|center|alt=Theoretical Moller Differential Cross-Section in Center of Mass Frame Frame|'''Figure 5a:''' The theoretical Moller electron differential cross-section for | + | [[File:Theory_new.png|frame|center|alt=Theoretical Moller Differential Cross-Section in Center of Mass Frame Frame|'''Figure 5a:''' The theoretical Moller electron differential cross-section for an incident 11 GeV(Lab) electron in the Center of Mass frame of reference.]] |
Converting the number of electrons scattered per angle theta to barns, we can use the relation | Converting the number of electrons scattered per angle theta to barns, we can use the relation | ||
| Line 67: | Line 67: | ||
Using the number of incident electrons, for 1 Moller electron: | Using the number of incident electrons, for 1 Moller electron: | ||
| − | <center><math>\frac{1}{\rho_{target}\times l_{target} \times | + | <center><math>\frac{1}{\rho_{target}\times l_{target} \times 6\times 10^7}=7.92\times 10^{-7} barns</math></center> |
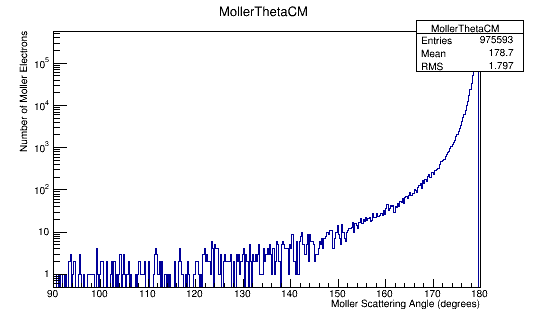
We can use this number to scale the number of electrons per angle to a differential cross-section in barns. Using the plot of the Moller electron scattering angle theta in the Center of Mass frame, | We can use this number to scale the number of electrons per angle to a differential cross-section in barns. Using the plot of the Moller electron scattering angle theta in the Center of Mass frame, | ||
| Line 76: | Line 76: | ||
<pre> | <pre> | ||
TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180); | TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180); | ||
| − | Combo->Add(MollerThetaCM, | + | Combo->Add(MollerThetaCM,7.92e-7); |
Combo->Draw(); | Combo->Draw(); | ||
Theory->Draw("same"); | Theory->Draw("same"); | ||
Revision as of 14:06, 4 April 2018
Using the equation from [1]
This can be simplified to the form
Plugging in the values expected for a scattering electron in the CM frame:
Using unit analysis on the term outside the parantheses, we find that the differential cross section for an electron at this momentum should be around
Using the conversion of
The trigonometric function part of the equation comes out to it's minimum of 9 at 90 degrees.
We find that the differential cross section scale is
Plotting the Moller Differential Cross-Section we find:
Converting the number of electrons scattered per angle theta to barns, we can use the relation
where ρtarget is the density of the target material, ltarget is the length of the target, and Iscattered is the number of incident particles scattered per time.
This gives, for LH2 in a 1cm long target:
Using the number of incident electrons, for 1 Moller electron:
We can use this number to scale the number of electrons per angle to a differential cross-section in barns. Using the plot of the Moller electron scattering angle theta in the Center of Mass frame,
We can rescale and combine the theoretical differential cross-section for one electron.
TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180);
Combo->Add(MollerThetaCM,7.92e-7);
Combo->Draw();
Theory->Draw("same");