2NCorr SPDP Introduction

go_back

The calculation of angular correlation

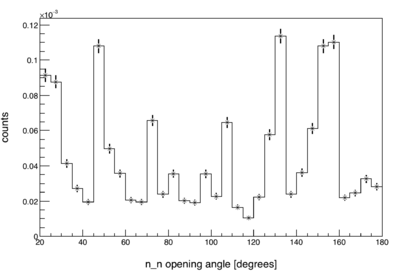
The neutron efficiency and acceptance of our detector array varies highly non-uniformly over the range of two-neutron opening angles ([math]\theta_{nn}[/math]). This is due to the detector array's non-spherically symmetric geometry, and to its varying neutron detection efficiency as a function of both position and energy (see figure).

• 

  Measured opening angle distribution of neutrons from the spontaneous fission of Cf252.

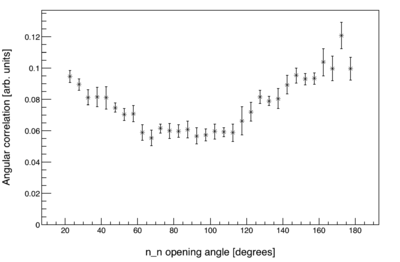
For this reason, every measured distribution is made meaningful by normalizing against a "control" distribution. This is done by diving the values of the measured distribution by the control distribution on a bin-by-bin basis.

two-neutron opening angle

For [math]\theta_{nn}[/math], the control distribution is made by looking at the events from pairs of two pulses, such that the the two pulses occurred within a few 100 ms of each other. If there is a neutron event in both of the pulses from a given pulse pair, then the opening angle between the two events is calculated. Since no information can be shared between the neutrons of different pulses, the control distribution must be free of any two-neutron correlations. However, the control distribution is still subject to the exact same effects of detector geometry and efficiency as is the distribution from pairs of truly correlated neutrons. So here, the words "angular correlation", refer to the measured [math]\theta_{nn}[/math] rate relative to a completely uncorrelated neutron source. The plot below is the same data from the plot above after normalization to the uncorrelated distribution.

• 

  Angular correlation between neutron pairs (E>1.5 MeV) from the SF of Cf252. In this case, instead of normalizing against neutrons from separate pulses, neutrons across separate SF fission events are used.

single-neutron absolute theta

Another measurement possible with this set up, is the distribution of the angle between neutron singles, and the direction of the incident photon beam ([math]\theta_{abs}[/math]). When constructing a distribution from neutron singles, the method of using uncorrelated neutron pairs from different pulses no longer works, because while the neutrons in a pair are uncorrelated with each other, they are both correlated with the direction of the incident photon beam. For this reason, neutron singles from the spontaneous fission (SF) of Cf252 are used for normalization. This choice leads to several issues, because there are differences in experimental conditions between the measurement of photo-neutrons in the presence of a photon beam, versus the measurement of neutrons from the SF of Cf252. The energy spectrum of neutrons from Cf252 differ from that of our photo-neutrons. During the Cf252 measurement, the detectors experience much dead-time caused by the detection of photons. Also, the noise profiles are very different. Each of these effects must be removed or neglected by employing various corrections and assumptions, which results in a analysis procedure that is less robust than the same-pulse different-pulse method.

Accidentals and trues

An accidental two-neutron coincidence, or accidental for short, is defined here as any pair of neutrons that are uncorrelated despite having been produced during the same pulse. An example is a neutron from a (gamma,n) reaction paired with a neutron from a (gamma, fiss) reaction. As another example, consider a pulse that causes two photofission events, such that the one fission releases four correlated neutrons and the other releases two, creating 4*2=8 possible distinct pairs of uncorrelated neutrons, or eight accidentals.

A true two-neutron coincidence, or true for short, is defined here as any pair correlated neutrons. For example, there are 4*3/2=6 trues created by a photofission event that releases 4 correlated neutrons.

During the experiment, measured trues/accidentals always occurred as two-neutron coincidences, since three or more neutrons were never detected in coincidence.

go_back