Lead Shield Cone

Target

We need to edit the EXn02DetectorConstruction file to allow for a target that is a lead cone to simulate the Moller Shield. The header file for an elliptical Cone gives the parameters need to call with.

// $Id: G4EllipticalCone.hh 67011 2013-01-29 16:17:41Z gcosmo $
//  
//    
// --------------------------------------------------------------------
// GEANT 4 class header file
//   
// G4EllipticalCone
// 
// Class description:
//
// G4EllipticalCone is a full cone with elliptical base which can be cut in Z.
//
// Member Data:
//
//      xSemiAxis       semi-axis, x, without dimentions
//      ySemiAxis       semi-axis, y, without dimentions
//      zheight         height, z
//      zTopCut         upper cut plane level, z
// 
// The height in Z corresponds to where the elliptical cone hits the
// Z-axis if it had no Z cut. Also the cone is centered at zero having a
// base at zTopCut and another at -zTopCut. The semi-major axes at the Z=0
// plane are given by xSemiAxis*zheight and ySemiAxis*zheight so that the
// curved surface of our cone satisfies the equation:
// 
// ***************************************************************************
// *                                                                         *
// *           (x/xSemiAxis)^2 + (y/ySemiAxis)^2 = (zheight - z)^2           *
// *                                                                         *
// ***************************************************************************
// 
// In case you want to construct G4EllipticalCone from :
//   1. halflength in Z = zTopCut
//   2. Dx and Dy =  halflength of ellipse axis  at  z = -zTopCut
//   3. dx and dy =  halflength of ellipse axis  at  z =  zTopCut
//      ! Attention :  dx/dy=Dx/Dy
// 
// You need to find xSemiAxis,ySemiAxis and zheight:
//
//  xSemiAxis = (Dx-dx)/(2*zTopCut)
//  ySemiAxis = (Dy-dy)/(2*zTopCut)
//    zheight = (Dx+dx)/(2*xSemiAxis)

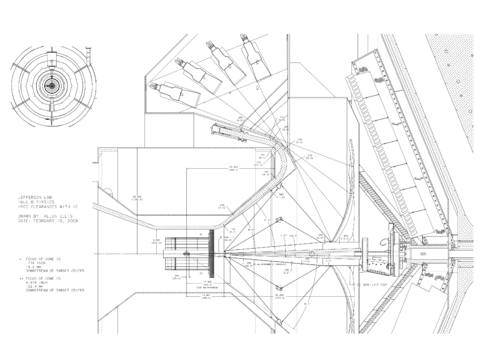
The geometry looks like

Solving the variables:

1. halflength in Z = zTopCut

The cone shape starts 380 cm from the vertex point of (0,0,0). It extends 1325.9 beyond the starting position. This gives the z(max) as z = 1705.9 cm. Since this cone is centered at the vertex with zTopCut positive and negative placed an equal distance from the vertex, 1325.9/2=662.95 cm

2. Dx and Dy = halflength of ellipse axis at z = -zTopCut

The length of the x and y components at the smaller end of the cone are found from the diameter at this position. Assuming a circle for the cross-cut, then x=y=0.5 dia= 43 cm /2 = 21.5 cm

3. dx and dy = halflength of ellipse axis at z = zTopCut

Using geometry, for a right triangle with it's apex at the vertex and a height of 1705.9, with an interior angle of 5 degrees.

[math]1705.9\ cm\ Tan\ 5^\circ=149.247\ cm[/math]

Solving for the variable to pass to the function:

[math] xSemiAxis = \frac{Dx-dx}{2*zTopCut}= \frac{21.5-149.247}{2*662.95}= \frac{-127.747}{1325.9}=-0.096=ySemiAxis [/math]

The height in z is defined at the the point where the cone vertex crosses the z=0 plane in x&y. From the drawing, the vertex is originally placed at 0,0,0. Since the GEANT4 cone is centered at a new vertex with the circular cross sections of the cone at +/- 662.95, and the distance from the first smaller cross section is 380, this gives the intersection at -1042.95 cm with respect to the new vertex.

[math]zheight = \frac{Dx+dx}{2*xSemiAxis}=\frac{21.5+149.247}{2*-0.096}=\frac{170.747}{-0.192}=-889.307[/math]

Particle Gun

mkdir ParticleGunInputs

root -l LUND_Spread_LH2_IsotropicPhi.C

split -d -l 3000 -a 3 LUND_Spread_LH2_IsotropicPhi.LUND LUND_Spread_LH2_IsotropicPhi_

prename 's/(LUND_Spread_LH2_IsotropicPhi_\d{3})/$1.LUND/' LUND_Spread_LH2_IsotropicPhi_*

Using the file LUND2ParticleGun.C 106 macros for the GEANT4 ParticleGun are created that mirror the LUND files. The same random number is initially input for each macro as was used for the LUND file.