Difference between revisions of "Initial CM Frame 4-momentum components"
Jump to navigation
Jump to search
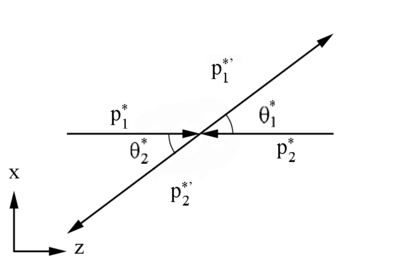
Figure 2: Definition of variables in the Center of Mass Frame
| Line 1: | Line 1: | ||
<center><math>\textbf{\underline{Navigation}}</math> | <center><math>\textbf{\underline{Navigation}}</math> | ||
| − | [[ | + | [[Initial_Lab_Frame_4-momentum_components|<math>\vartriangleleft </math>]] |
[[VanWasshenova_Thesis#Initial_4-momentum_Components|<math>\triangle </math>]] | [[VanWasshenova_Thesis#Initial_4-momentum_Components|<math>\triangle </math>]] | ||
[[Special_Case_of_Equal_Mass_Particles|<math>\vartriangleright </math>]] | [[Special_Case_of_Equal_Mass_Particles|<math>\vartriangleright </math>]] | ||
Revision as of 22:31, 15 June 2017
Initial CM Frame 4-momentum components

Starting with the definition for the total relativistic energy:
Since we can assume that the frame of reference is an inertial frame, it moves at a constant velocity, the mass should remain constant.
We can use 4-momenta vectors, i.e. ,with c=1, to describe the variables in the CM Frame.
Using the fact that the scalar product of a 4-momenta with itself,
is invariant.
Using this notation, the sum of two 4-momenta forms a 4-vector as well
The length of this four-vector is an invariant as well