|
|
| Line 64: |
Line 64: |
| | | | |
| | | | |
| − | <center><math>s+t \equiv 4m^2</math></center> | + | <center><math>s+t_{max} \equiv 4m^2</math></center> |
| | | | |
| | | | |
| | | | |
| − | <center><math>\Rightarrow t=4m^2-s</math></center> | + | <center><math>\Rightarrow t_{max}=4m^2-s</math></center> |
| | | | |
| | | | |
| | | | |
| − | <center><math>t=4m^2-4m^2- 4p \ ^{*2}</math></center> | + | <center><math>t_{max}=4m^2-4m^2- 4p \ ^{*2}</math></center> |
| | | | |
| | | | |
| | | | |
| − | <center><math>t=-4p \ ^{*2}</math></center> | + | <center><math>t_{max}=-4p \ ^{*2}</math></center> |
| | | | |
| | | | |
Revision as of 17:35, 12 June 2017
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
Limits based on Mandelstam Variables
Since the Mandelstam variables are the scalar product of 4-momenta, which are invariants, they are invariants as well. The sum of these invariant variables must also be invariant as well. Find the sum of the 3 Mandelstam variables when the two particles have equal mass in the center of mass frame gives:
[math]s+t+u=(4(m^2+ p \ ^{*2}))+(-2 p \ ^{*2}(1-cos\ \theta))+(-2 p \ ^{*2}(1+cos\ \theta))[/math]
[math]s+t+u \equiv 4m^2[/math]
Since
[math]s \equiv 4(m^2+\vec p \ ^{*2})[/math]
This implies
[math]s \ge 4m^2[/math]
In turn, this implies
[math] t \le 0 \qquad u \le 0[/math]
At the condition both t and u are equal to zero, we find
[math] t = 0 \qquad u = 0[/math]
[math]-2 p \ ^{*2}(1-cos\ \theta) = 0 \qquad -2 p \ ^{*2}(1+cos\ \theta) = 0[/math]
[math](-2 p \ ^{*2}+2 p \ ^{*2}cos\ \theta) = 0 \qquad (-2 p \ ^{*2}-2 p \ ^{*2}cos\ \theta) = 0[/math]
[math]2 p \ ^{*2}cos\ \theta = 2 p \ ^{*2} \qquad -2 p \ ^{*2}cos\ \theta = 2 p \ ^{*2}[/math]
[math]\cos\ \theta = 1 \qquad \cos\ \theta = -1[/math]
[math]\Rightarrow \theta_{t=0} = \arccos \ 1=0^{\circ} \qquad \theta_{u=0} = \arccos \ -1=180^{\circ}[/math]
Holding u constant at zero we can find the maximum of t
[math]s+t_{max} \equiv 4m^2[/math]
[math]\Rightarrow t_{max}=4m^2-s[/math]
[math]t_{max}=4m^2-4m^2- 4p \ ^{*2}[/math]
[math]t_{max}=-4p \ ^{*2}[/math]
[math]-2 p \ ^{*2}(1-cos\ \theta)=-4p \ ^{*2}[/math]
[math](1-cos\ \theta)=2[/math]
[math]-cos\ \theta=1[/math]
[math] \theta_{max} \equiv \arccos -1[/math]
The domain of the arccos function is from −1 to +1 inclusive and the range is from 0 to π radians inclusive (or from 0° to 180°). This implies for arccos -1, the range will include imaginary numbers. Knowing that the range of the cosine function is -1 to +1 inclusive and the domain to be any angle
[math]z = \arccos{-1}[/math]
[math]\cos{z} = \cos{\arccos{-1}}[/math]
[math]\cos{z} = 3[/math]
From Euler's formula
[math]\cos{x} = \frac{e^{i z} + e^{-i z}}{2}[/math]
[math] \frac{e^{i z} + e^{-i z}}{2} = 3[/math]
[math] e^{i z} + e^{-i z} = 6[/math]
Multiply with [math]e^{i z}[/math]
[math]e^{2i z} + 1 = 6e^{i z}[/math]
Letting [math]y = e^{i z}[/math]
We get an quadratic equation:
[math]y^2 - 6y + 1 = 0[/math]
[math]y = (6 ± √32)/2[/math]
[math]y_1 = 5.828427 = e^{i z}[/math]
[math]y_2 = 0.171573 = e^{i z}[/math]
Apply the natural log on both sides gives the solution for arccos 3:
[math]z_1 = \frac{ln(5.828427) }{ i}=-1.76275i[/math]
[math] z_2 = \frac{ln(0.171573) }{ i}=1.76275i[/math]
Converting to polar coordinates:
[math]r \equiv |z|=sqrt{z^2}=1.76275[/math]
Since
[math]z \equiv a+bi[/math]
[math]\theta \equiv \arctan{\frac{\pm b}{a}}=\pm 90^{\circ}[/math]
Since there is only an imaginary component.
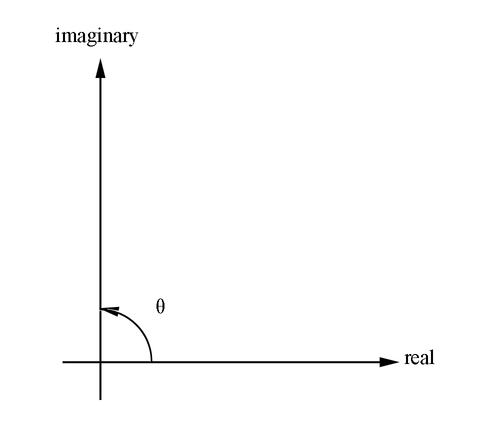
Figure 2.1: Angle theta measured with respect to imaginary plane.
